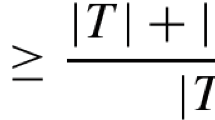Abstract.
The Sperner product of the digraphs and is the digraph whose vertex set is the Cartesian product of the vertex set of the two, while there is an arc in pointing from to if either or both of the relations and hold. We study the growth of the largest transitively oriented clique in the Sperner powers of a fixed graph G and derive the first non-trivial upper bounds on the Sperner capacity of arbitrary digraphs.
Similar content being viewed by others
Author information
Authors and Affiliations
Rights and permissions
About this article
Cite this article
Körner, J. On Clique Growth in Products of Directed Graphs. Graphs Comb 14, 25–36 (1998). https://doi.org/10.1007/s003730050012
Issue Date:
DOI: https://doi.org/10.1007/s003730050012