Construction of Hamiltonian Cycles in Layered Cubic Planar Graphs

Abstract.

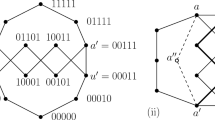
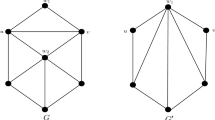
 In this paper, a class of cubic planar graphs is given that have Hamiltonian cycles that can be constructed in linear time. A member of this class is called a layered cubic planar graph, and consists of a sequence of cycles C ₀ ,C ₁ ,…,C _n such that each pair of successive cycles, C _i , C _i+1 , is joined by a matching. The cycles can be pictured as concentric circles, and the edges of the matchings as radial line segments between successive circles. The subgraph bounded by two successive cycles forms a layer; each face in layer i is incident to a fixed number k _i+1 of edges in the matching in layer i+1. The problem that initially motivated this work is that of identifying classes of convex cubic polyhedra that can be easily edge three-colored.