Abstract.
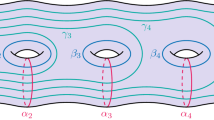
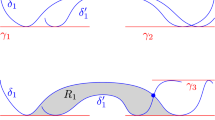
We prove that for every family of n pairwise intersecting simple closed planar curves in general position, at least (4/5)n 2−O(n) points lie on more than one curve. This improves the previous lower bound of (3/4)n 2−O(n) due to Richter and Thomassen.
This is a preview of subscription content, log in via an institution to check access.
Similar content being viewed by others
Author information
Authors and Affiliations
Additional information
Received: March 29, 2000 Final version received: August 30, 2001
RID="*"
ID="*" Research supported in part by NSF grant DMS-9970325
Acknowledgments. I thank Bruce Richter for informing me about this problem, Gelasio Salazar for reading a preliminary version of the paper, and a Referee for useful comments.
Current Address: Microsoft Research, One Microsoft Way, Redmond, WA 98052-6399, USA. e-mail: mubayi@microsoft.com
1991 Mathematics Subject Classification. 05C35, 52C10
Rights and permissions
About this article
Cite this article
Mubayi* , D. Intersecting Curves in the Plane. Graphs Comb 18, 583–589 (2002). https://doi.org/10.1007/s003730200042
Issue Date:
DOI: https://doi.org/10.1007/s003730200042