Neural network firing-rate models on integral form

Abstract

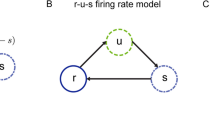
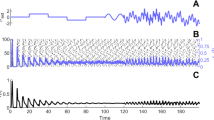
Firing-rate models describing neural-network activity can be formulated in terms of differential equations for the synaptic drive from neurons. Such models are typically derived from more general models based on Volterra integral equations assuming exponentially decaying temporal coupling kernels describing the coupling of pre- and postsynaptic activities. Here we study models with other choices of temporal coupling kernels. In particular, we investigate the stability properties of constant solutions of two-population Volterra models by studying the equilibrium solutions of the corresponding autonomous dynamical systems, derived using the linear chain trick, by means of the Routh–Hurwitz criterion. In the four investigated synaptic-drive models with identical equilibrium points we find that the choice of temporal coupling kernels significantly affects the equilibrium-point stability properties. A model with an α-function replacing the standard exponentially decaying function in the inhibitory coupling kernel is in most of our examples found to be most prone to instability, while the opposite situation with an α-function describing the excitatory kernel is found to be least prone to instability. The standard model with exponentially decaying coupling kernels is typically found to be an intermediate case. We further find that stability is promoted by increasing the weight of self-inhibition or shortening the time constant of the inhibition.