Abstract
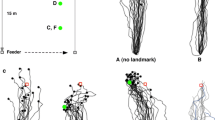
The ability to locomote is a defining characteristic of all animals. Yet, all but the most trivial forms of navigation are poorly understood. Here we report and discuss the analytical results of an in-depth study of a simple navigation problem. In principle, there are two strategies for navigating a straight course. One is to use an external directional reference and to continually reorient with reference to it. The other is to monitor body rotations from internal sensory information only. We showed previously that, at least for simple representations of locomotion, the first strategy will enable an animal or mobile agent to move arbitrarily far away from its starting point, but the second strategy will not do so, even after an infinite number of steps. This paper extends and generalizes the earlier results by demonstrating that these findings are true even when a very general model of locomotion is used. In this general model, error components within individual steps are not independent, and directional errors may be biased. In the absence of a compass, the expected path of a directed walk in general approximates a logarithmic spiral. Some examples are given to illustrate potential applications of the quantitative results derived here. Motivated by the analytical results developed in this work, a nomenclature for directed walks is proposed and discussed. Issues related to path integration in mammals and robots, and measuring the curvature of a noisy path are also addressed using directed walk theory.
Similar content being viewed by others
References
Atkinson RPD, Rhodes CJ, MacDonald DW, Anderson RM (2002) Scale-free dynamics in the movement patterns of jackals. Oikos 98: 134–140
Barlow HB, Levick WR (1965) The mechanism of directionally selective units in rabbit’s retina. J Physiol 178: 477–504
Barry C, Hayman R, Burgess N, Jeffery KJ (2007) Experience-dependent rescaling of entorhinal grids. Nat Neurosci 10: 682–684
Bartumeus F, Peters F, Pueyo S, Marrasé C, Catalan J (2003) Helical Lévy walks: adjusting searching statistics to resource availability in microzooplankton. Proc Nat Acad Sci USA 100: 12771–12775
Batschelet E (1981) Circular statistics in biology. Academic Press, London
Berg HC (1983) Random walks in biology. Academic Press, New York
Bovet P, Benhamou S (1988) Spatial analysis of animals’ movements using a correlated random walk model. J Theor Biol 131: 419–433
Bracher C (2004) Eigenfunction approach to the persistent random walk in two dimensions. Phys A 331: 448–466
Brown CT, Liebovitch LS, Glendon R (2007) Lévy flights in Dobe Júhoanso foraging patterns. Hum Ecol 35: 129–138
Brown R (1828) A brief account of microscopical observations made in the months of June, July and August, 1827, on the particles contained in the pollen of plants; and on the general existence of active molecules in organic and inorganic bodies. Edinburgh New Philos J, pp 358–371
Byers J (2001) Correlated random walk equations of animal dispersal resolved by simulation. Ecology 82(6): 1680–1690
Cheung A, Zhang SW, Stricker C, Srinivasan MV (2007) Animal navigation: the difficulty of moving in a straight line. Biol Cybern 97: 47–61
Claes I, Van den Broeck (1987) Random walk with persistence. J Stat Phys 49: 383–393
Collett TS, Rees JA (1997) View-based navigation in hymenoptera: multiple strategies of landmark guidance in the approach to a feeder. J Comp Physiol A 181: 47–58
Dacke M, Nilsson D-E, Scholtz C, Byrne M, Warrant EJ (2003) Animal behaviour: insect orientation to polarized moonlight. Nature 424: 33
Dudchenko PA, Bruce C (2005) Navigation without landmarks: can rats use a sense of direction to return to a home site?. Connect Sci 17: 107–125
Einstein A (1905) On the motion, required by the molecular kinetic theory of heat, of small particles suspended in stationary liquid. Ann Physik 17: 549–560
Etienne AS, Maurer R, Berlie J, Reverdin B, Rowe T, Georgakopoulos J, Séguinot V (1998) Navigation through vector addition. Nature 396: 161–164
Etienne AS, Maurer R, Séguinot V (1996) Path integration in mammals and its interaction with visual landmarks. J Exp Biol 199: 201–209
Grey DR (1989) Persistent random walks may have arbitrarily large tails. Adv Appl Prob 21: 229–230
Gothard KM, Skaggs WE, McNaughton BL (1996) Dynamics of mismatch correction in the hippocampal ensemble code for space: Interaction between path integration and environmental cues. J Neurosci 16: 8027–8040
Hafting T, Fyhn M, Molden S, Moser M-B, Moser EI (2005) Microstructure of a spatial map in the entorhinal cortex. Nature 436: 801–806
Horn BKP, Schunck B (1981) Determining optical flow. Artif Intell 17: 185–203
Ingemar JC (1991) Blanche—an experiment in guidance and navigation of an autonomous robot vehicle. IEEE Trans Robot Autom 7: 193–204
Jeffery KJ (2007) Integration of the sensory inputs to place cells: what, where, why, and how?. Hippocampus 17: 775–785
Jeffery KJ, Anand RL, Anderson MI (2006) A role for terrain slope in orienting hippocampal place fields. Exp Brain Res 169: 218–225
Kareiva PM, Shigesada N (1983) Analyzing insect movement as a correlated random walk. Oecologia 56: 234–238
Kreyszig E (1993) Advanced engineering mathematics. Wiley, Singapore
Larralde H (1997) Transport properties of a two-dimensional “chiral” persistent random walk. Phys Rev E 56: 5004–5008
McCulloch CE, Cain ML (1989) Analyzing discrete movement data as a correlated random walk. Ecology 70(2): 383–388
Malkiel B (1973) A random walk down Wall Street. W W Norton & Company Inc., New York
Mantegna RN, Stanley HE (1994) Stochastic process with ultraslow convergence to a Gaussian: the truncated Lévy flight. Phys Rev Lett 73: 2946–2949
Marsh LM, Jones RE (1988) The form and consequences of random walk movement models. J Theor Biol 133: 113–131
McNaughton BL, Battaglia FP, Jensen O, Moser EI, Moser M-B (2006) Path integration and the neural basis of the “cognitive map”. Nat Rev Neurosci 7: 663–678
Milford MJ (2008) Robot navigation from nature. Springer Tracts in Advanced Robotics, vol 41
Milford MJ, Wyeth G, Prasser D (2006) RatSLAM on the edge: revealing a coherent representation from an overloaded rat brain. IEEE/RSJ international conference on intelligent robots and systems, IEEE, pp 4060–4065
Mittelstaedt H, Mittelstaedt ML (1982) Homing by path integration. In: Papi F, Wallraff HG (eds) Avian navigation. Springer, Berlin, pp 290–297
Nossal R, Weiss G (1974) A descriptive theory of cell migration on surfaces. J Theor Biol 47: 103–113
O’Keefe J, Burgess N (1996) Geometric determinants of the place fields of hippocampal neurons. Nature 381: 425–428
O’Keefe J, Nadel L (1978) The hippocampus as a cognitive map. Clarendon Press, Oxford
Quirk GJ, Muller RU, Kubie JL (1990) The firing of hippocampal place cells in the dark depends on the rat’s recent experience. J Neurosci 10: 2008–2017
Pearson K (1905a) The problem of the random walk. Nature 72: 294
Pearson K (1905b) The problem of the random walk. Nature 72: 342
Ramos-Fernández G, Mateos JL, Miramontes O, Cocho G, Larralde H, Ayala-Orozco B (2004) Lévy walk patterns in the foraging movements of spider monkeys (Ateles geoffroyi). Behav Ecol Sociobiol 55: 223–230
Rayleigh (1905) The problem of the random walk. Nature 72: 318
Reichardt W (1961) Autocorrelation, a principle for the evaluation of sensory information by the central nervous system. In: Rosenblith W (eds) Sensory communication. MIT Press/Wiley, Cambridge/New York, pp 465–493
Reynolds AM, Smith AD, Menzel R, Greggers U, Reynolds DR, Riley JR (2007) Displaced honey bees perform optimal scale-free search flights. Ecology 88: 1955–1961
Rosenblatt M (1956) Remarks on some nonparametric estimates of a density function. Ann Math Stat 27: 832–835
Save E, Nerad L, Poucet B (2000) Contribution of multiple sensory information to place field stability in hippocampal place cells. Hippocampus 10: 64–76
Shlesinger MF (1995) Comment on “Stochastic process with ultraslow convergence to a Gaussian: the truncated Lévy flight”. Phys Rev Lett 74: 4959
Srinivasan MV (1990) Generalized gradient schemes for the measurement of two-dimensional image motion. Biol Cybern 63: 421–431
Srinivasan MV (1994) An image-interpolation technique for the computation of optic flow and egomotion. Biol Cybern 71: 401–415
Tchen CM (1952) Random flight with multiple partial correlations. J Chem Phys 20: 214–217
Thrun S (1997) To know or not to know: on the utility of models in mobile robots. AI Mag 18: 47–54
Thrun S (2003) Robotic mapping: a survey. In: Lakemeyer G, Nebel B (eds) Exploring artifical intelligence in the new millenium. Morgan Kaufmann, San Francisco, pp 1–35
Viswanathan GM, Afanasyev V, Buldyrev SV, Murphy EJ, Prince PA, Stanley HE (1996) Lévy flight search patterns of wandering albatrosses. Nature 381: 413–415
Viswanathan GM, Buldyrev SV, Havlin S, da Luz MGE, Raposo EP, Stanley HE (1999) Optimizing the success of random searches. Nature 401: 911–914
Wehner R (1992) Arthropods. In: Papi F (eds) Animal homing. Chapman and Hall, London, pp 45–144
Wehner R (1994) The polarization-vision project: championing organismic biology. Fortschr Zool 39: 103–143
Wiltschko W, Wiltschko R (2005) Magnetic orientation and magnetoreception in birds and other animals. J Comp Physiol A 191(8): 675–693
Wu H, Li BL, Springer TA, Neill WH (2000) Modelling animal movement as a persistent random walk in two dimensions: expected magnitude of net displacement. Ecol Model 132: 115–124
Author information
Authors and Affiliations
Corresponding author
Electronic Supplementary Material
The Below is the Electronic Supplementary Material.
Rights and permissions
About this article
Cite this article
Cheung, A., Zhang, S., Stricker, C. et al. Animal navigation: general properties of directed walks. Biol Cybern 99, 197–217 (2008). https://doi.org/10.1007/s00422-008-0251-z
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00422-008-0251-z
Keywords
- Navigation
- Compass
- Cumulative errors
- Sensory noise
- Motor noise
- Directed walk
- Elementary step
- General
- Simple
- Bias
- Path integration
- Straightness
- Curvature
- Correlated random walk
- Persistent random walk
- Logarithmic spiral
- Dead reckoning
- Vectorial navigation
- Central limit theorem
- Positional moments
- Mean position
- Expected position
- Positional variance
- Axis of intended locomotion