Skip to main content

Advertisement

Springer Nature Link
Log in

Stability switches, oscillatory multistability, and spatio-temporal patterns of nonlinear oscillations in recurrently delay coupled neural networks

  • Original Paper
  • Published:
Biological Cybernetics Aims and scope Submit manuscript

Abstract

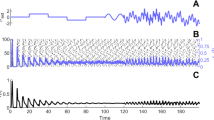
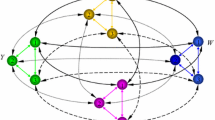
A model of time-delay recurrently coupled spatially segregated neural assemblies is here proposed. We show that it operates like some of the hierarchical architectures of the brain. Each assembly is a neural network with no delay in the local couplings between the units. The delay appears in the long range feedforward and feedback inter-assemblies communications. Bifurcation analysis of a simple four-units system in the autonomous case shows the richness of the dynamical behaviors in a biophysically plausible parameter region. We find oscillatory multistability, hysteresis, and stability switches of the rest state provoked by the time delay. Then we investigate the spatio-temporal patterns of bifurcating periodic solutions by using the symmetric local Hopf bifurcation theory of delay differential equations and derive the equation describing the flow on the center manifold that enables us determining the direction of Hopf bifurcations and stability of the bifurcating periodic orbits. We also discuss computational properties of the system due to the delay when an external drive of the network mimicks external sensory input.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  • Braitenberg V, Schuz A (1998) Cortex: statistics and geometry of neuronal connectivity. Springer, Berlin

    Google Scholar 

  • Bruce IC, Tatton WG (1980) Sequential output-input maturation of kitten motor cortex. Exp Brain Res 39: 411–419

    Article  PubMed  CAS  Google Scholar 

  • Bungay S, Campbell SA (2007) Patterns of oscillation in a ring of identical cells with delayed coupling. Int J Bifurcat Chaos 17: 3109–3125

    Article  Google Scholar 

  • Campbell SA, Edwards R, Van den Driessche P (2004) Delayed coupling between two neural network loops. SIAM J Appl Math 65: 316–335

    Article  Google Scholar 

  • Campbell SA, Yuan Y, Bungay SD (2005) Equivariant Hopf bifurcation in a ring of identical cells with delayed coupling. Nonlinearity 18: 2827–2846

    Article  Google Scholar 

  • Castellanos NP, Malmierca E, Nuñez A, Makarov VA (2007) Corticofugal modulation of the tactile response coherence of projecting neurons in the gracilis nucleus. J Neurophysiol 98: 2537–2549

    Article  PubMed  Google Scholar 

  • Chow S-N, Hale JK (1982) Methods of bifurcation theory. Springer, New York

    Google Scholar 

  • Engelborghs K, Luzyanina T, Samaey G (2001) DDE-BIFTOOL v. 2.00: a Matlab package for bifurcation analysis of delay differential equations. Technical Report TW-330, Department of Computer Science, K.U. Leuven, Leuven, Belgium

  • Ernst U, Pawelzik K, Geisel T (1995) Synchronization induced by temporal delays in pulse-coupled oscillators. Phys Rev Lett 74: 1570–1573

    Article  PubMed  CAS  Google Scholar 

  • Faria T, Magalháes LT (1995a) Normal form for retarded functional differential equations with parameters and applications to Hopf bifurcation. J Differ Equ 122: 181–200

    Article  Google Scholar 

  • Faria T, Magalháes LT (1995b) Normal form for retarded functional differential equations and applications to Bogdanov–Takens singularity. J Differ Equ 122: 201–224

    Article  Google Scholar 

  • Fuchs A, Haken H (1988) Pattern recognition and associative memory as dynamical processes in nonlinear systems. Neural Netw 1: 217–224

    Google Scholar 

  • Gerstner W (1996) Rapid phase locking in systems of pulse-coupled oscillators with delay. Phys Rev Lett 76: 1755–1758

    Article  PubMed  CAS  Google Scholar 

  • Golubitsky M, Stewart I, Schaeffer D (2003) Singularities and groups in bifurcation theory, vol II. Springer, New York

  • Guo S (2005) Spatio-temporal patterns of nonlinear oscillations in an excitatory ring network with delay. Nonlinearity 18: 2391–2407

    Article  Google Scholar 

  • Guo S (2007) Stability of nonlinear waves in a ring of neurons with delays. J Differ Equ 236: 343–374

    Article  Google Scholar 

  • Guo S, Huang L (2003) Hopf bifurcating periodic orbits in a ring of neurons with delays. Physica D 183: 19–44

    Article  Google Scholar 

  • Hale JK, Verduyn Lunel SM (1993) Introduction to functional differential equations. Springer, New York

    Google Scholar 

  • Hildebrand C, Skoglund S (1971) Calibre spectra of some fibre tract in the feline central nervous system during postnatal development. Acta Physiol Scand (Suppl) 364: 5–41

    CAS  Google Scholar 

  • Huang L, Wu J (2003) Nonlinear waves in networks of neurons with delayed feedback: pattern formation and continuation. SIAM J Math Anal 34: 836–860

    Article  Google Scholar 

  • Ikeda K, Matsumoto K (1987) High-dimensional chaotic behavior in systems with time-delayed feedback. Physica D 29: 223–235

    Article  Google Scholar 

  • Jabbur SJ, Towe AL (1961) Analysis of the antidromic cortical response following stimulation at the medullary pyramids. J Physiol 155: 148–160

    PubMed  CAS  Google Scholar 

  • Kandel ER, Schwartz JH, Jessell TM (2000) Principles of neural science, 4th edn. McGraw-Hill, New York

    Google Scholar 

  • Kuang Y (1994) Delay differential equations with applications in population dynamics. Academic Press, Boston

    Google Scholar 

  • Makarov VA, Makarova J, Herreras O (2009) Deconvolution of local field potential sources by independent component analysis. J Comput Neurosci (submitted)

  • Mallet-Paret J, Yorke JA (1982) Oriented families of periodic orbits, their sources, sinks and continuation. J Differ Equ 43: 419–450

    Article  Google Scholar 

  • Malmierca E, Castellanos NP, Nunez A, Makarov VA, Nuñez A (2009) Neuron synchronization in the rat gracilis nucleus facilitates sensory transmission in the somatosensory pathway. Eur J Neurosci (accepted)

  • Marcus CM, Westervelt RM (1989) Stability of analog neural networks with delay. Phys Rev A 39: 347–359

    Article  PubMed  Google Scholar 

  • Niebur E, Schuster HG, Kammen D (1991) Collective frequencies and metastability in networks of limit-cycle oscillators with time delay. Phys Rev Lett 67: 2753–2756

    Article  PubMed  Google Scholar 

  • Nuñez A, Malmierca E (2007) Corticofugal modulation of sensory information. Advances in anatomy embryology and cell biology, vol 187. Springer, Berlin

  • Purpura DP (1973) Analysis of morphophysiological developmental processes in mammalian brain. Res Publ Assoc Nerv Ment Dis 51: 79–110

    CAS  Google Scholar 

  • Ramana Reddy DV, Sen A, Johnston GL (1998) Time delay induced death in coupled limit cycle oscillators. Phys Rev Lett 80: 5109–5112

    Article  CAS  Google Scholar 

  • Ramana Reddy DV, Sen A, Johnston GL (1999) Time delay effects on coupled limit cycle oscillators at Hopf bifurcation. Physica D 129: 15–34

    Article  Google Scholar 

  • Ruan S (2001) Absolute stability, conditional stability and bifurcation in Kolmogorov-type predator-prey systems with discrete delays. Q Appl Math 59: 159–173

    Google Scholar 

  • Schuster HG, Wagner P (1989) Mutual entrainment of two limit cycle oscillators with time delayed coupling. Prog Theor Phys 81: 939–945

    Article  Google Scholar 

  • Seunghwan K, Seon H, Ryu CS (1997) Multistability in coupled oscillator systems with time delay. Phys Rev Lett 79: 2911–2914

    Article  Google Scholar 

  • Song Y, Han M, Peng Y (2004) Stability and Hopf bifurcations in a competitive Lotka-Volterra system with two delays. Chaos Solitons Fractals 22: 1139–1148

    Article  Google Scholar 

  • Song Y, Han M, Wei J (2005) Stability and Hopf bifurcation analysis on a simplified BAM neural network with delays. Physica D 200: 185–204

    Article  Google Scholar 

  • Song Y, Wei J, Yuan Y (2007) Stability switches and Hopf bifurcations in a pair of delay-coupled oscillators. J Nonlinear Sci 17: 145–166

    Article  Google Scholar 

  • Timme M, Wolf F, Geisel T (2002a) Prevalence of unstable attractors in networks of pulse-coupled oscillators. Phys Rev Lett 89: 154105-1-4

    Google Scholar 

  • Timme M, Wolf F, Geisel T (2002b) Coexistence of regular and irregular dynamics in complex networks of pulse-coupled oscillators. Phys Rev Lett 89: 258701-1-4

    Google Scholar 

  • Valverde F (1966) The pyramidal tract in rodents. A study of its relations with the posterior column nuclei, dorsolateral reticular formation of the medulla, and cervical spinal cord (Golgi and E.M. observations). Zeit f Zellforsch 71: 297–363

    Article  Google Scholar 

  • Wei J, Velarde MG (2004) Bifurcation analysis and existence of periodic solutions in a simple neural network with delays. Chaos 14: 940–953

    Article  PubMed  CAS  Google Scholar 

  • Wei J, Velarde MG, Makarov VA (2002) Oscillatory phenomena and stability of periodic solutions in a simple neural network with delay. Nonlinear Phenom Complex Syst 5: 407–417

    Google Scholar 

  • Wen Q, Chklovskii DB (2005) Segregation of the brain into gray and white matter: A design minimizing conduction delays. PLoS Comput Biol 1: 617–630

    Article  CAS  Google Scholar 

  • Wu J (1998) Symmetric functional-differential equations and neural networks with memory. Trans Am Math Soc 350: 4799–4838

    Article  Google Scholar 

  • Wu J, Faria T, Huang YS (1999) Synchronization and stable phase-locking in a network of neurons with memory. Math Comput Model 30: 117–138

    Article  Google Scholar 

  • Yordanova J, Kolev V (1997) Developmental changes in the event-related EEG theta response and P300. Electroencephalogr Clin Neurophysiol 104: 418–430

    Article  PubMed  CAS  Google Scholar 

  • Yuan Y (2007) Dynamics in a delayed-neural network. Chaos Solitons Fractals 33: 443–454

    Article  Google Scholar 

  • Yuan Y, Campbell SA (2004) Stability and synchronization of a ring of identical cells with delayed coupling. J Dyn Differ Equ 16: 709–744

    Article  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Instituto Pluridisciplinar, Universidad Complutense, Paseo Juan XXIII, 1, 28040, Madrid, Spain

    Yongli Song, Valeri A. Makarov & Manuel G. Velarde

  2. Department of Mathematics, Tongji University, 200092, Shanghai, China

    Yongli Song

  3. Depto. de Matemática Aplicada, Facultad de Matemáticas, Universidad Complutense, Avda. Complutense s/n, 28040, Madrid, Spain

    Valeri A. Makarov

Authors
  1. Yongli Song
    View author publications

    You can also search for this author inPubMed Google Scholar

  2. Valeri A. Makarov
    View author publications

    You can also search for this author inPubMed Google Scholar

  3. Manuel G. Velarde
    View author publications

    You can also search for this author inPubMed Google Scholar

Corresponding author

Correspondence to Valeri A. Makarov.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Song, Y., Makarov, V.A. & Velarde, M.G. Stability switches, oscillatory multistability, and spatio-temporal patterns of nonlinear oscillations in recurrently delay coupled neural networks. Biol Cybern 101, 147–167 (2009). https://doi.org/10.1007/s00422-009-0326-5

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00422-009-0326-5

Keywords