Macroscopic neural mass model constructed from a current-based network model of spiking neurons

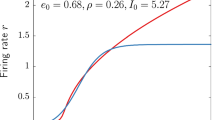
Abstract

Neural mass models (NMMs) are efficient frameworks for describing macroscopic cortical dynamics including electroencephalogram and magnetoencephalogram signals. Originally, these models were formulated on an empirical basis of synaptic dynamics with relatively long time constants. By clarifying the relations between NMMs and the dynamics of microscopic structures such as neurons and synapses, we can better understand cortical and neural mechanisms from a multi-scale perspective. In a previous study, the NMMs were analytically derived by averaging the equations of synaptic dynamics over the neurons in the population and further averaging the equations of the membrane-potential dynamics. However, the averaging of synaptic current assumes that the neuron membrane potentials are nearly time invariant and that they remain at sub-threshold levels to retain the conductance-based model. This approximation limits the NMM to the non-firing state. In the present study, we newly propose a derivation of a NMM by alternatively approximating the synaptic current which is assumed to be independent of the membrane potential, thus adopting a current-based model. Our proposed model releases the constraint of the nearly constant membrane potential. We confirm that the obtained model is reducible to the previous model in the non-firing situation and that it reproduces the temporal mean values and relative power spectrum densities of the average membrane potentials for the spiking neurons. It is further ensured that the existing NMM properly models the averaged dynamics over individual neurons even if they are spiking in the populations.

Appendix: Input power and cross spectra

This appendix derives Eq. (35), which computes the power and cross-spectrum densities of the input noises $\tilde{\phi }_{{\mathrm X}_{\mathrm E}}(t)$ and $\tilde{\phi }_{{\mathrm X}_{\mathrm I}}(t)$ imposed on the excitatory and inhibitory populations, respectively. Every Poisson spike train $\zeta _i(t)$ in Eq. (29), firing at the rate given by Eq. (30), matches the definition of Mazzoni et al. (2008), beim Graben and Rodrigues (2013), and Cavallari et al. (2014).

The Poisson spike train of a neuron is approximated by white Gaussian noise, which is averaged over the neurons of a population. The ensemble mean of the inhomogeneous Poisson process $\zeta _i(t)$ with time-varying rate $\rho (t)=\rho _0+\eta (t)$ for the i-th neuron is expressed as

$$\begin{aligned} { \left\langle {\zeta _i(t)}\right\rangle =\left\langle {\sqrt{\rho (t)}\xi _i(t)+\rho (t)}\right\rangle , } \end{aligned}$$

(37)

where $\xi _i(t)$ is white Gaussian noise with zero mean and unit variance (Moreno-Bote et al. 2008). As the white Gaussian noise $\xi _i(t)$ is orthogonal to the probability process $\eta (t)$ in Eq. (30), we can compute the ensemble mean, representing white Gaussian noise with a time-varying mean of $\rho _0+\eta (t)$ and variance of $\rho _0$:

$$\begin{aligned} \left\langle {\zeta _i(t)}\right\rangle= & {} \left\langle {\sqrt{\rho _0+\eta (t)}\xi _i(t)+\rho _0+\eta (t)}\right\rangle \nonumber \\\simeq & {} \sqrt{\rho _0}\left\langle { \left( 1+\frac{\eta (t)}{2\rho _0}\right) \xi _i(t) +\rho _0+\left\langle {\eta (t)}\right\rangle }\right\rangle \nonumber \\\simeq & {} \sqrt{\rho _0}\left\langle {\xi _i(t)}\right\rangle +\rho _0+\left\langle {\eta (t)}\right\rangle {,} \end{aligned}$$

(38)

where averaging over the neurons in the population $\mu$ decreases the variance by a factor of $1/N_\mu$ for $\mu \in \{{\mathrm E},{\mathrm I}\}$. Accordingly, the standard deviation $\sqrt{\rho _0}$, i.e., a coefficient of $\left\langle {\xi _i(t)}\right\rangle$, decreases to $\sqrt{\rho _0/N_\mu }$. The average noise of the population $\mu$ is given by

$$\begin{aligned} { \left\langle {\tilde{\phi }_{{\mathrm X}_\mu }(t)}\right\rangle \simeq \sqrt{\frac{\rho _0}{N_\mu }}\left\langle {\xi _\mu (t)}\right\rangle +\rho _0+\left\langle {\eta (t)}\right\rangle {,} } \end{aligned}$$

(39)

where $\xi _\mu (t)$ is white Gaussian noise with zero mean and unit variance such that this noise is independent of $\xi _i(t)$ for any i. Therefore, the correlation function between the average noises for the Poisson processes of neuron populations $\mu$ and $\nu$, $\{\mu ,\nu \}\in \{{\mathrm {E}}, {\mathrm {I}}\}$, respectively, is given by

$$\begin{aligned} \left\langle {\tilde{\phi }_\mathrm {X_\mu }(t)\tilde{\phi }_{{\mathrm X}_\nu }(t+\tau )}\right\rangle= & {} \frac{\rho _0}{\sqrt{N_\mu N_\nu }}\left\langle {\xi _\mu (t)\xi _\nu (t+\tau )}\right\rangle \nonumber \\&\quad +\rho _0^2+\left\langle {\eta (t)\eta (t+\tau )}\right\rangle . \end{aligned}$$

(40)

The spectrum density is straightforwardly solved as the Fourier transform of the correlation function:

$$\begin{aligned}&\frac{1}{2\pi }\tilde{\phi }_{{\mathrm X}_\mu }[-\mathrm {i}\omega ]\tilde{\phi }_{{\mathrm X}_\nu }[\mathrm {i}\omega ] \nonumber \\&\qquad = \frac{1}{2\pi }\int _{-\infty }^\infty \left\langle {\tilde{\phi }_{{\mathrm X}_\mu }(t)\tilde{\phi }_{{\mathrm X}_\nu }(t+\tau )}\right\rangle e^{-\mathrm {i}\omega \tau }d\tau . \end{aligned}$$

(41)

The result is Eq. (35). Note that the final term,

$$\begin{aligned}&\frac{1}{2\pi }\int _{-\infty }^\infty \left\langle {\eta (t)\eta (t+\tau )}\right\rangle e^{-\mathrm {i}\omega \tau }d\tau \nonumber \\&\quad = \frac{1}{2\pi }\bigl |\eta [\mathrm {i}\omega ]\bigr |^2 = \frac{\epsilon _{\mathrm X}\sigma _{\mathrm X}^2}{\pi \left( 1+\epsilon _{\mathrm X}^2\omega ^2\right) }, \end{aligned}$$

(42)

is the PSD of the OU process $\eta (t)$.

Finally, we estimate the order of magnitude of each term in Eq. (35). Except at extremely high frequencies, the first term is negligibly small even in the nonzero case $\mu =\nu$. In the network model of neurons (as in Mazzoni et al. 2008), we set $\rho _0 \sim 1$ spikes/ms, $\epsilon _{\mathrm X}\sim 10$ ms, $\sigma _{\mathrm X}^2\sim 0.1$ spikes/ms, and $N_{\mathrm I}\sim 1000$. At frequencies below 100 Hz, i.e., $\rho _0/(2\pi {N_\mu })<0.1$ kHz, the orders of magnitude of the respective terms are

$$\begin{aligned}&{ \frac{\rho _0}{2\pi {N_\mu }} \sim \frac{1}{2\pi {N_\mu }}<\frac{1}{2\pi N_{\mathrm I}} \sim 10^{-3}, } \end{aligned}$$

(43)

$$\begin{aligned}&{ \rho _0^2\delta (\omega )\sim \delta (\omega ), \, S_{\eta \eta }(\omega ) \sim \frac{0.1\times 10}{\pi (1+10^2\times 0.1^2)}\sim 1. } \end{aligned}$$

(44)

Therefore, in this frequency band, the first term is approximately 1000 times smaller than the other terms in Eq. (35), and accordingly, the PSD was approximately obtained as Eq. (36).