Abstract
Contrary to forward biomechanical functions, which are deterministic, inverse biomechanical functions are generally not. Calculating an inverse biomechanical function is an ill-posed problem, which has no unique solution for a manipulator with several degrees of freedom. Studies of the command and control of biological movements suggest that the cerebellum takes part in the computation of approximate inverse functions, and this ability can control fast movements by predicting the consequence of current motor command. Limb movements toward a goal are defined as fast if they last less than the total duration of the processing and transmission delays in the motor and sensory pathways. Because of these delays, fast movements cannot be continuously controlled in a closed loop by use of sensory signals. Thus, fast movements must be controlled by some open loop controller, of which cerebellar pathways constitute an important part. This article presents a system-level fuzzy neuronal motor control circuit, inspired by the cerebellar pathways. The cerebellar cortex (CC) is assumed to embed internal models of the biomechanical functions of the limb segments. Such neural models are able to predict the consequences of motor commands and issue predictive signals encoding movement variables, which are sent to the controller via internal feedback loops. Differences between desired and expected values of variables of movements are calculated in the deep cerebellar nuclei (DCN). After motor learning, the whole circuit can approximate the inverse function of the biomechanical function of a limb and acts as a controller. In this research, internal models of direct biomechanical functions are learned and embedded in the connectivity of the cerebellar pathways. Two fuzzy neural networks represent the two parts of the cerebellum, and an online gradual learning drives the acquisition of the internal models in CC and the controlling rules in DCN. As during real learning, exercise and repetition increase skill and speed. The learning procedure is started by a simple and slow movement, controlled in the presence of delays by a simple closed loop controller comparable to the spinal reflexes. The speed of the movements is then increased gradually, and output error signals are used to compute teaching signals and drive learning. Repetition of movements at each speed level allows to properly set the two neural networks, and progressively learn the movement. Finally, conditions of stability of the proposed model as an inverter are identified. Next, the control of a single segment arm, moved by two muscles, is simulated. After proper setting by motor learning, the circuit is able to reject perturbations.







Similar content being viewed by others
References
Albus JS (1975a) Data storage in the cerebellar model articulation controller (CMAC). J Dyn Syst Meas Control 97:228–233
Albus JS (1975b) A new approach to manipulator control: the cerebellar model articulation controller (CMAC). J Dyn Syst Meas Control 97:220–227
Armano S, Rossi P, Taglietti V, D’Angelo E (2000) Long-term potentiation of intrinsic excitability at the mossy fiber-granule cell synapse of rat cerebellum. J Neurosci 20(14):5208–5216
Asadi-Eydivand M, Ebadzadeh M, Solati-Hashjin M, Darlot C, Osman N (2015) Cerebellum-inspired neural network solution of the inverse kinematics problem. Biol Cybern 109:561–574
Barto AG, Fagg AH, Sitkoff N, Houk JC (1999) A cerebellar model of timing and prediction in the control of reaching. Neural Comput 11:565–594
Bostan AC, Dum RP, Strick PL (2013) Cerebellar networks with the cerebral cortex and basal ganglia. Trends Cogn Sci 17(4):241–254. doi:10.1016/j.tics.2013.03.003
Chapeau-Blondeau P, Chauvet G (1991) A neural network model of the cerebellar cortex performing dynamic associations. Biol Cybern 65:267–279
D’Angelo E, Solinas S, Mapelli J, Gandolfi D, Mapelli L, Prestori F (2013) The cerebellar Golgi cell and spatiotemporal organization of granular layer activity. Front Neural Circuits 7(93):1–21
Darban ZZ, Ebadzadeh M (2012) Anatomical model of VOR using fuzzy neural network. Proc Eng 41:561–566
Darlot C (1993) The Cerebellum as a predictor of neural messages—I. The stable estimator hypothesis. Neuroscience 56:617–646
Darlot C, Zupan L, Etard O, Denise P, Maruani A (1996) Computation of inverse dynamics for the control of movements. Biol Cybern 75:173–186
Denise P, Darlot C (1993) The cerebellum as a predictor of neural messages—II. Role in motor control and motion sickness. Neuroscience 56(3):647–655
Droulez J, Darlot C (1990) The geometric and dynamic implications of the coherence constraints in three-dimensional sensorimotor inter-actions. In: Jeannerod M (ed) Attention and performance XIII. Lawrence Erlbaum, Hillsdale, pp 495–526
Ebadzadeh M, Darlot C (2003) Cerebellar learning of bio-mechanical functions of extra-ocular muscles: modeling by artificial neural networks. Neuroscience 122:941–966
Ebadzadeh M, Salimi-Badr A (2015) CFNN: correlated fuzzy neural network. Neurocomputing 148:430–444
Ebadzadeh M, Salimi-Badr A (2017) IC-FNN: a novel fuzzy neural network with interpretable intuitive and correlated-contours fuzzy rules for function approximation. IEEE Trans Fuzzy Syst. doi:10.1109/TFUZZ.2017.2718497
Ebadzadeh M, Tondu B, Darlot C (2005) Computation of inverse functions in a model of cerebellar and reflex pathways allows to control a mobile mechanical segment. Neuroscience 133:29–49
Eccles JC, Ito M, Szentágothai J (1967) The cerebellum as a neuronal machine. Springer, New York
Eskiizmirliler S, Forestier N, Tondu B, Darlot C (2002) A model of the cerebellar pathways applied to the control of a single-joint robot arm actuated by McKibben artificial muscles. Biol Cybern 86:379–394
Forestier N (1999) Modélisation du contrôle moteur cérébelleux par réseaux de neurones formels. Thèse de doctorat. Ecole Nationale Supérieure des Télécommunications. ENST 99 E 009
Fujita M (1982) Adaptive filter model of the cerebellum. Biol Cybern 45:195–206
Garrido J, Luque NR, D’Angelo E, Ros E (2013) Distributed cerebellar plasticity implements adaptable gain control in a manipulation task: a closed-loop robotic simulation. Front Neural Circuits 7(159):1–20
Gentili RJ, Papaxanthis C, Ebadzadeh M, Eskiizmirliler S, Ouanezar S, Darlot C (2009) Integration of gravitational torques in cerebellar pathways allows for the dynamic inverse computation of vertical pointing movements of a robot arm. PloS ONE 4:e5176
Han H, Qiao J (2010) A self-organizing fuzzy neural network based on a growing and pruning algorithm. IEEE Trans Fuzzy Syst 18:1129–1143
Hirano T (2013) Long-term depression and other synaptic plasticity in the cerebellum. Proc Jpn Acad Ser B Phys Biol Sci 89(4):183–195
Houk JC, Buckingham JT, Barto AG (1996) Models of the cerebellum and motor control. Behav Brain Sci 19:368–383
Huang G, Saratchandran P, Sundararajan N (2005) A generalized growing and pruning RBF (GGAP-RBF) neural network for function approximation. IEEE Trans Neural Netw 16:57–67
Ito M (1986) Long-term depression as a memory process in the cerebellum. Neurosci Res 3:531–539
Ito M (2006) Cerebellar circuitry as a neuronal machine. Prog Neurobiol 78:272–303
Ito M, Kano M (1982) Long-lasting depression of parallel fiber-Purkinje cell transmission induced by conjunctive stimulation of parallel fibers and climbing fibers in the cerebellar cortex. Neurosci Lett 33:253–258
Jaberi J, Gambrell K, Tiwana P, Madden C, Finn R (2013) Long-term clinical outcome analysis of poly-methyl methacrylate cranio-plasty for large skull defects. J Oral Maxillofac Surg 71:e81–e88
Jaeger D (2013) Cerebellar nuclei and cerebellar learning. Handbook of the cerebellum and cerebellar disorders. Springer, Berlin
Kandel E, Schwartz J (2013) Principles of neural science, 5th edn. McGraw-Hill Education, New York
Kawato M, Gomi H (1992) A computational model of four regions of the cerebellum based on feedback-error learning. Biol Cybern 68:95–103
Kawato M, Furukawa K, Suzuki R (1987) A hierarchical neural-network model for control and learning of voluntary movement. Biol Cybern 57:169–185
Khayat O, Ebadzadeh M, Shahdoosti H, Rajaei R, Khajehnasiri I (2009) A novel hybrid algorithm for creating self-organizing fuzzy neural networks. Neurocomputing 73:517–524
Koene A, Erkelens C (2002) Cause of kinematic differences during centrifugal and centripetal saccades. Vis Res 42:1797–1808
Kosko B (1994) Fuzzy systems as universal approximators. IEEE Trans Comput 43:1329–1333
Luque NR, Garrido JA, Carrillo RR, D’Angelo E, Ros E (2014) Fast convergence of learning requires plasticity between inferior olive and deep cerebellar nuclei in a manipulation task: a closed-loop robotic simulation. Front Comput Neurosci 8(97):1–16
Malek H, Ebadzadeh MM, Rahmati M (2012) Three new fuzzy neural networks learning algorithms based on clustering, training error and genetic algorithm. Appl Intell 37:280–289
Mapelli J, D’Angelo E (2005) The spatial organization of long-term synaptic plasticity at the input stage of cerebellum. J Neurosci 25:1285–1296
Marr D (1969) A theory of cerebellar cortex. J Physiol 202:437–470
Miall R (1998) The cerebellum, predictive control andmotor coordination. Sens Guid Mov 218:272–290
Miall R, Wolpert DM (1996) Forward models for physiological motor control. Neural Netw 9:1265–1279
Miall R, Weir D, Wolpert D, Stein J (1993) Is the cerebellum a Smith predictor? J Mot Behav 25:203–216
Nieus T, Sola E, Mapelli J, Saftenku E, Rossi P, D’Angelo E (2006) LTP regulates burst initiation and frequency at mossy fiber-granule cell synapses of rat cerebellum: experimental observations and theoretical predictions. J Neurophysiol 95:686–699
Ouanezar S, Jean F, Tondu B, Maier M, Darlot C, Eskiizmirliler S (2011) Biologically inspired sensory motor control of a 2-link robotic arm actuated by McKibben muscles. In: Proceedings of the IEEE international conference on robotics and automation. Shanghai International Conference Center, Shanghai
Passino M, Yurkovich S (1998) Fuzzy control. Addison-Wesley, Reading
Riahi-Madvar H, Ayyoubzadeh S, Khadangi E, Ebadzadeh M (2009) An expert system for predicting longitudinal dispersion coefficient in natural streams by using ANFIS. Expert Syst Appl 36:8589–8596
Roggeri L, Rivieccio B, Rossi P, D’Angelo E (2008) Tactile stimulation evokes long-term synaptic plasticity in the granular layer of cerebellum. J Neurosci 28:6354–6359
Rubio JJ (2009) SOFMLS: online self organizing fuzzy modified least squares network. IEEE Trans Fuzzy Syst 17:1296–1309
Schweighofer N, Lang EJ, Kawato M (2013) Role of the olivo-cerebellar complex in motor learning and control. Front Neural Circuits 7:94. doi:10.3389/fncir.2013.00094
Shadmehr R (2009) Computational approaches to motor control. Encyclopedia of Neuroscience Oxford, vol 3. Academic Press, New York, pp 9–17
Shadmehr R, Krakauer J (2008) A computational neuroanatomy for motor control. Exp Brain Res 185:359–381
Uttley A (1979) Information transmission in the nervous system. Academic Press, New York
Uusisaari M, Knopfel T (2011) Functional classification of neurons in the mouse lateral cerebellar nuclei. Cerebellum 10:637–646
Wang N, Er MJ, Meng X (2009) A fast and accurate online self-organizing scheme for parsimonious fuzzy neural networks. Neurocomputing 72:3818–3829
Wolpert DM, Miall RC, Kawato M (1998) Internal models in the cerebellum. Trends Cogn Sci 2:338–347
Xu WL, Zhang NY, Zeng K (2000) A comparative study on sufficient conditions for Takagi-Sugeno fuzzy systems as universal approximators. IEEE Trans Fuzzy Syst 8(5):773–780
Ying H (1998) General SISO Takagi-Sugeno fuzzy systems with linear rule consequent are universal approximators. IEEE Trans Fuzzy Syst 6(4):582–587
Author information
Authors and Affiliations
Corresponding author
Appendices
Appendix 1: Stability
The conditions of stability of the system are hereafter studied by the linearization method. The motor command signal \(\alpha \) and the forward biomechanical function F are approximated by Taylor’s expansions. The results show that the stability domain depends on the current state of the system x(t), the current motor command \(\alpha (t)\), and the value of an adjustable coefficient K. Stability can be preserved, provided the value of K is dynamically set at any time.
At time t, the system is assumed to be in equilibrium and the motor command signal to be \(\alpha _{{0}}\). Linearization of the function of the motor order by Taylor’s expansion around the equilibrium gives:
The equation can be derived for a next step:
From (A-1) and (A-2), it comes:
This relation can be recurrently generalized for any step n to the next one:
According to (A-4), after a little deviation from the equilibrium point \(\alpha _{{0}}\) at time t, the system can return to equilibrium if, after n steps, the following equation is satisfied:
So, based on (A-4) and (A-5), the following equation must be satisfied:
Because of the deviation from the equilibrium point at time t, the value \(\alpha (t)\) is not equal to \(\alpha _{{0}}\); so the following equation must be satisfied:
and considering n as a positive integer number, the following condition is derived:
Considering the structure of the circuit, this equation can be rewritten as:
where \(F^{*}\) approximates F, the forward biomechanical function of the limb.
If \(K = 1\), the following condition is derived from (A-9):
Appendix 2: Value of coefficient K
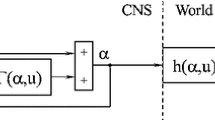
Assume that the biomechanical function F of the limb can be approximated at any time by a linear system and that a neural network embeds an inner representation \(F^{*}\). Assume also that the feedback and motor pathways have some small, but not negligible transmission delays: \({D}_{{1}}\) in the feedback pathway, which transmits an efference copy of the motor order, and \({D}_{{2}}\) in the motor pathway from the CNS to the motoneurones, which innervate the muscles of the limb. The circuit shown in Fig. 1 translates into a structure the equations in the Laplace space (Fig. 8). A Taylor’s expansion of \({D}_{{i}}=\mathrm{e}^{-Ds}\), the Laplace transform of a time delay \({D}_{{i}}\), allows to approximate \({D}_{{i}}\) by \({1-}{D}_{{i}}{\cdot }{s}\).
From the desired position \(\theta ^{\mathrm{D}}\), two equations determine the motor command \(\alpha \) and the actual position \(\theta ^{\mathrm {A}}\):
From (A-12), the desired angular position \(\theta ^{\mathrm{D}}\) can be calculated as:
If an approximate inverse function is actually computed, the desired and actual angular positions are equal:
So, based on (A-11), (A-13) and (A-14), the following equation is derived:
A value of K, suitable to approximate the inverse function; can be deduced:
By considering the error E between F and \(F^{*}\) equal to \(E = F - F^{*}\), the above equation can be rewritten as:
So the proposed structure can compute an approximate inverse function of the biomechanical function, provided that the time-dependent coefficient K be dynamically set to a suitable value.
Appendix 3: Structure of fuzzy neural networks
FNNs with a 5-layer structure stand for the neuronal networks of the cerebellar cortex (CC) and deep cerebellar nuclei (DCN) (Fig. 9).
A fuzzy neural network with dynamic structure shaping (Grown and Prune). The inputs to the Rule Generator neuron are the signals from the input layer (via track no. 1), the output signals of the fuzzy rule layer (via track no. 1), and the error signal measuring the difference between the desired and the actual outputs (via track no. 3). If the coverage of the incoming information by the fuzzy rules is insufficient (this being measured by comparison to a predefined threshold value), the Rule Generator neuron adds new fuzzy rules. This can be interpreted as activating inactive neurons (granular cells in the cerebellar cortex)
The layers of such FNNs process signals according to precise rules:
-
1. Input layer This first layer receives an input vector with n dimensions \({X} = [{x}_{{1}}, {x}_{{2}}, \ldots , {x}_{{n}}]^{\mathrm{T}}\), which it projects to the neurons of the second layer (Fuzzy Sets layer) and to the rule generator neuron.
-
2. Fuzzy sets layer The neurons of this layer compute the membership function of input vector received from the Input Layer for different fuzzy sets defined in this layer. Therefore, their output, \(\mu _{ij}\) is defined as follows, for the ith rule and jth input dimension:
$$\begin{aligned} \mu _{ij}=\mathrm{e}^{-\left( \frac{x_{j}-m_{ij}}{\sigma _{ij}} \right) ^{2}} \end{aligned}$$(A-18)where \(m_{ij}\) is the center and \(\sigma _{ij}\) is the width parameter of the ith rule for the jth input dimension.
-
3. Fuzzy rules layer The neurons of this layer combine the inputs from the Fuzzy Sets Layer and project the final value as the membership value of the input vector to a fuzzy rule. Considering R as the number of fuzzy rules the output of this layer is defined as below:
$$\begin{aligned} \varphi _{i}=\prod \limits _{j=1}^n \mu _{ij} =\mathrm{e}^{-\sum \nolimits _{j=1}^n {\, \left( \frac{x_{j}-m_{ij}}{\sigma _{ij}} \right) }^{2} } \end{aligned}$$(A-19) -
4. Fuzzy rule generator layer The unique neuron of this layer receives inputs from three origins: 1. From the input layer, a copy of the current sample of input signals.
2. From the fuzzy rules layer, copies of signals which re-code, by fuzzy rules, the current sample of input signals.
3. From a comparing element, a signal coding the movement error, and used as a teaching signal.
In the fuzzy rules layer, input signals are recoded into “fuzzy signals”, which are compared to a suitable threshold in the Generator neuron. If the “fuzzy signals” are lower than the threshold, this means that the current input vector is not completely represented by the current set of fuzzy rules. If at the same time, the error is significant, this coincidence shows that the coverage of the “inputs space” by the “fuzzy space” is insufficient. To improve this coverage, adding new fuzzy rules is necessary. Thus, the generator neuron sends teaching signals to the neurons of the Membership Function Layer. New fuzzy rules are added by a process comparable to an activation of granular cells, or useless rules are removed by a process comparable to a deactivation. This procedure of structure learning ensures an appropriate coverage of the space of input vectors by the fuzzy rules so that the “inputs space” is well represented in the “fuzzy space” (Rubio 2009; Wang et al. 2009; Han and Qiao 2010; Malek et al. 2012).
These three entries to the generator neuron are shown in Fig. 9:
-
1.
Input sample (Blue lines, with number 1) The input sample is sent to the generator neuron.
-
2.
Outputs of the Fuzzy Rules Layer (Green lines, with number 2) The coverage of the current input sample \(\varPhi \) by the fuzzy rules is calculated as:
$$\begin{aligned} \varPhi =\sum \limits _{i=1}^R \varphi _{i} \end{aligned}$$(A-20)A fuzzy rule is to be added if, simultaneously, the coverage of the input signals by the fuzzy rules \(\varPhi \) is insufficient and a significant error is measured.
-
3.
The error signal (Red line with number 3) A comparing element calculates the movement error. If this error is significant, and the coverage of the current input sample by the fuzzy rules is insufficient, then adding a supplementary fuzzy rule could help to reduce the error.
A new rule is added to cover the part of the input space which is not represented precisely enough. A logical choice to cover this part of the input space, is to set the center of the new fuzzy rule—the mean value of the Gaussian curve—at the mean of the input sample which is insufficiently coded (Huang et al. 2005; Rubio 2009; Wang et al. 2009; Han and Qiao 2010; Malek et al. 2012) (Fig. 7).
The available input sample is used to calculate the center of the new fuzzy rule ((\(R+{1})\)th fuzzy rule), and its width is a fixed vector as follows:
5. Output layer This layer consists in only one linear neuron, which receives inputs signals from the fuzzy rules layer. It calculates their weighted linear sum, which is the final output of the network:
where the vector of synaptic weights is \({W} = [{w}_{{1}},{w}_{{2}}, \ldots , {w}_{{R}}]^{\mathrm {T}}\), and y is the final output.
Appendix 4: Range of values of K ensuring stability
When the learning of \(F^{*}\) is achieved and the parameters of this function remain constant, based on the definition of the output of the FNN and on the result exposed in “Appendix 1”, it comes:
where \(\alpha _{t}\) and \(x_{t}\) are respectively the input motor order and the state of the system at time t.
Now, based on the definition of the FNN, the following equation can be calculated:
where \(m_{i\alpha }\) and \(\sigma _{i\alpha }\) are the center and width of the membership function related to the ith rule.
Stability is ensured if K remains in a range of values depending on the state of the system at any time t, according to the rules:
Appendix 5: Biomechanical function
The simulated limb is a one-segment arm with two artificial muscles, based on the Hill model of muscle, inspired by a model proposed for the eye (Koene and Erkelens 2002). Its state equations are written in the discrete time and its biomechanical function is controlled in discrete time. Index 1 denotes the variables of the biomechanics of the agonist muscle and index 2 those of the biomechanics of the antagonistic muscle.
Notations \(\alpha _{{i}}\) is the motor order sent to the \(i{\mathrm {th}}\) muscle, \(l_{{i}}\) is the length of the \(i\mathrm{{th}}\) muscle, \(F_{\mathrm{ai}}\) is the active force for the \(i\mathrm{{th}}\) muscle, \(F_{r}\) is the resistance force, Ks and \(K_{r}\) are constants and \(\tau _{1}\), \(\tau _{2}\) and \(\tau _{3}\) are time constants, \(\sigma \) is the recruitment and activation time constant of the low-pass filter producing \(F_{a}\), H is the Hill constant, \(\delta \) is the sampling period, J is the moment inertia, \(\alpha _{0}\) is the rest-activity of the motor neurones, \(\varOmega \) is the torque and \(\ddot{\theta }\) is the angular acceleration.
The equations of the biomechanical system are:

The values used in this study are presented in Table 3.
Rights and permissions
About this article
Cite this article
Salimi-Badr, A., Ebadzadeh, M.M. & Darlot, C. Fuzzy neuronal model of motor control inspired by cerebellar pathways to online and gradually learn inverse biomechanical functions in the presence of delay. Biol Cybern 111, 421–438 (2017). https://doi.org/10.1007/s00422-017-0735-9
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00422-017-0735-9