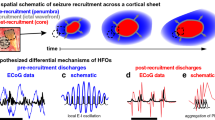
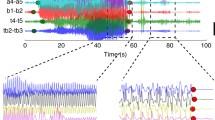
Abstract
The effect of gap junctions as well as the biological mechanisms behind seizure wave propagation is not completely understood. In this work, we use a simple neural field model to study the possible influence of gap junctions specifically on cortical wave propagation that has been observed in vivo preceding seizure termination. We consider a voltage-based neural field model consisting of an excitatory and an inhibitory population as well as both chemical and gap junction-like synapses. We are able to approximate important properties of cortical wave propagation previously observed in vivo before seizure termination. This model adds support to existing evidence from models and clinical data suggesting a key role of gap junctions in seizure wave propagation. In particular, we found that in this model gap junction-like connectivity determines the propagation of one-bump or two-bump traveling wave solutions with features consistent with the clinical data. For sufficiently increased gap junction connectivity, wave solutions cease to exist. Moreover, gap junction connectivity needs to be sufficiently low or moderate to permit the existence of linearly stable solutions of interest.








Similar content being viewed by others
References
Amari S (1977) Dynamics of pattern formation in lateral-inhibition type neural fields. Biol Cybern 27:77–87
Braitenberg V, Schuz A (1998) Cortex: statistics and geometry of neuronal connectivity. Springer, Berlin
Bressloff P (2012) Spatiotemporal dynamics of continuum neural fields. J Phys A Math Theor 45(3):033001
Bressloff P (2016) Diffusion in cells with stochastically gated gap junctions. SIAM J Appl Math 76:1658–1682
Bressloff P, Cowan J, Golubitsky M, Thomas P, Wiener M (2001) Geometric visual hallucinations, euclidean symmetry and the functional architecture of striate cortex. Philos Trans R Soc B 356:299–330
Carlen P, Skinner F, Zhang L, Naus C, Kushnir ea M (2000) The role of gap junctions in seizures. Brain Res Rev 32:235–241
Chen L, Meng M (1995) Compact and scattered gap junctions in diffusion mediated cell–cell communication. J Theor Biol 176:39–45
Chow C, Kopell N (2000) Dynamics of spiking neurons with electrical coupling. Neural Comput 12:1643–1678
Coombes S (2005) Waves, bumps, and patterns in neural field theories. Biol Cybern 93:91–108
Coombes S (2008) Neuronal networks with gap junctions: a study of piecewise linear planar neuron models. SIAM J Appl Dyn Syst 7:1101–1129
Coombes S, Zachariou M (2009) Gap junctions and emergent rhythms. In: Josic K, Rubin J, Matias M, Romo R (eds) Coherent behavior in neuronal networks. Springer series in computational neuroscience, vol 3. Springer, New York, NY
Coombes S, Beim Graben P, Potthast R, Wright J (2014) Neural fields: theory and applications. Springer, Berlin
Dudek F, Yasamura T, JE R (1998) Non-synaptic mechanisms in seizures and epileptogenesis. Cell Biol Int 22:793–805
Elvin A (2008) Pattern formation in a neural field model. PhD thesis, Massey University, College of Sciences
Ermentrout G (1998) Neural networks as spatio-temporal pattern-forming systems. Rep Prog Phys 61:353–430
Ermentrout G (2006) Gap junctions destroy persistent states in excitatory networks. Phys Rev E Stat Nonlinear Soft Matter Phys 74:031918
Ermentrout G, Cowan J (1979) A mathematical theory of visual hallucination patterns. Biol Cybern 34:137–150
Ermentrout G, Terman D (2010) Mathematical foundations of neuroscience. Springer, Berlin
Evangelista E, Benar C, Bonini F, Carron R, Colombet B, Regis J, Bartolomei F (2015) Does the thalamo-cortical synchrony play a role in seizure termination? Front Neurol 6:192
Evans L (2010) Partial differential equations, 2nd edn. American Mathematical Society, Providence
Evans W, Martin P (2002) Gap junctions: structure and function. Mol Membr Biol 19:121–136
Foster B, Boja I, Liley D (2011) Understanding the effects of anesthetic agents on the EEG through neural field theory. In: Conference proceedings of IEEE engineering in medicine and biology society, vol 652
Frascoli F, Van Veen L, Bojak I, Liley D (2011) Metabifurcation analysis of a mean field model of the cortex. Physica D 240:949–962
Fujii Y, Maekawa S, Morita M (2017) Astrocyte calcium waves propagate proximally by gap junction and distally by extracellular diffusion of ATP released from volume-regulated anion channels. Sci Rep 7:13115
Fukuda T, Kosaka T, Singer W, Galuske R (2006) Gap junctions among dendrites of cortical gabaergic neurons establish a dense and widespread intercolumnar network. J Neurosci 26(13):3434–3443
González-Ramírez L, Kramer M (2018) The effect of inhibition on the existence of traveling wave solutions for a neural field model of human seizure termination. J Comput Neurosci 44(3):393–409
González-Ramírez L, Ahmed O, Cash S, Wayne C, Kramer M (2015) A biologically constrained, mathematical model of cortical wave propagation preceding seizure termination. PLoS Comput Biol 11:e1004065
Goodenough D, Paul D (2009) Gap junctions. Cold Spring Harb Perspect Biol 1:a002576
Jin M, Chen Z (2011) Role of gap junctions in epilepsy. Neurosci Bull 27(6):389–406
Jirsa VK, Stacey WC, Quilichini PP, Ivanov I, Bernard C (2014) On the nature of seizure dynamics. Brain 137:2210–2230
Kapitula T, Kutz N, Sandstede B (2004) The evans function for nonlocal equations. Indiana Univ Math J 53:1095–1126
Keener J, Sneyd J (1998) Mathematical physiology. Springer, New York
Kepler T, Marder E, Abbott L (1990) The effect of electrical coupling on the frequency of model neuronal oscillators. Science 248:83–85
Kopell N, Ermentrout B (2004) Chemical and electrical synapses perform complementary roles in the synchronization of interneuronal networks. Proc Natl Acad Sci USA 101:15482–15487
Lacar B, Young S, Platel J, Bordey A (2011) Gap junction-mediated calcium waves define communication networks among murine postnatal neural progenitor cells. Eur J Neurosci 34(12):1895–1905
Laing C (2015) Exact neural fields incorporating gap junctions. SIAM J Appl Dyn Syst 14(4):1899–1929
Lewis T, Rinzel J (2003) Dynamics of spiking neurons connected by both inhibitory and electrical coupling. J Comput Neurosci 14:283–309
Liley D, Cadusch P, Dafilis M (2002) A spatially continuous mean field theory of electrocortical activity. Network 13:67–113
Martinet LE, Fiddyment G, Madsen JR, Eskandar EN, Truccolo W, Eden UT, Cash SS, Kramer MA (2017) Human seizures couple across spatial scales through travelling wave dynamics. Nat Commun 8:14896
Mylvaganam S, Ramani M, Krawczyk M, Carlen P (2014) Roles of gap junctions, connexins, and pannexins in epilepsy. Front Physiol 5:172
Perucca P, Dubeau F, Gotman J (2013) Intracranial electroencephalographic seizure-onset patterns: effect of underlying pathology. Brain 137:183–96
Peyrache A, Dehghani N, Eskandar E et al (2012) Spatiotemporal dynamics of neocortical excitation and inhibition during human sleep. PNAS 109(5):1731–1736
Proix T, Jirsa VK, Bartolomei F, Guye M, Wilson T (2018) Predicting the spatiotemporal diversity of seizure propagation and termination in human focal epilepsy. Nat Commun 9:1088
Reimann M, Anastassiou C, Perin R, Hill S, Markram H et al (2013) A biophysically detailed model of neocortical local field potentials predicts the critical role of active membrane currents. Neuron 79:375–390
Rose B, Loewenstein W (1976) Permeability of a cell junction and the local cytoplasmic free ionised calcium concentration; a study with aequorin. J Membr Biol 28:87–119
Saez J, Connor J, Spray D, Bennett M (1989) Hepatocyte gap junctions are permeable to the second messenger, inositol 1,4,5-trisphosphate, and to calcium ions. Proc Natl Acad Sci USA 86:2708–2712
Sandstede B (2002) Stability of travelling waves. Handb Dyn Syst 2:983–1055
Sandstede B (2007) Evans function and nonlinear stability of traveling waves in neuronal network models. Int J Bifurc Chaos 17:2693–2704
Schevon CA, Weiss SA, McKhann G, Goodman RR, Yuste R, Emerson RG, Trevelyan AJ (2012) Evidence of an inhibitory restraint of seizure activity in humans. Nat Commun 3:1060
Schmitz D, Schuchmann S, Fisahn A, Draguhn A, Buhl E et al (2001) Axo-axonal coupling: a novel mechanism for ultrafast neuronal communication. Neuron 31(5):831–840
Sherman A, Rinzel J (1992) Rhythmogenic effects of weak electrotonic coupling in neuronal models. Proc Nat Acad Sci USA 89:2471–2474
Smith EH, Liou JY, Davis TS, Merricks EM, Kellis SS, Weiss SA, Greger B, House PA, McKhann GM, Goofman RR, Emerson RG, Bateman LM, Trevelyan AJ, Schevon CA (2016) The ictal wavefront is the spatiotemporal source of discharges during spontaneous human seizures. Nat Commun 7:11098
Stakgold I, Holst M (2011) Green’s functions and boundary value problems, 3rd edn. Wiley, New Jersey
Steyn-Ross M, Steyn-Ross D, Wilson M, Sleigh JW (2007) Gap junctions mediate large-scale turing structures in a mean-field cortex driven by subcortical noise. Phys Rev E 76:011916
Steyn-Ross M, Steyn-Ross D, Sleigh JW (2012) Gap junctions modulate seizures in a mean field-model of general anesthesia for the cortex. Cogn Neurodyn 6:215–225
Weiss SA, Banks GP, McKhann GMJ, Goodman RR, Emerson RG, Trevelyan AJ, Schevon C (2013) Ictal high frequency oscillations distinguish two types of seizure territories in humans. Brain 136:3796–808
Wilson H, Cowan J (1972) Excitatory and inhibitory interactions in localized populations of model neurons. Biophys J 12:1–24
Zhang M, Ladas T, Qiu C, Shivacharan R, Gonzalez-Reyes L, Durand D (2014) Propagation of epileptiform activity can be independent of synaptic transmission, gap junctions, or diffusion and is consistent with electrical field transmission. J Neurosci 34(4):1409–1419
Zhao X, Robinson P (2015) Generalized seizures in a neural field model with bursting dynamics. J Comput Neurosci 39:197–216
Author information
Authors and Affiliations
Corresponding author
Additional information
Communicated by Benjamin Lindner.
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
LRGR acknowledges support from SIP-IPN 20195566.
Appendices
A Appendix: Model motivation
A biophysically based and widely used model for describing the somatic membrane potential \(V_i(t)\) of a single neuron is Ermentrout (1998); Bressloff (2012):
where C is the cell capacitance, \(I_{\text {con}}\) is the membrane current, \(I_{\text {syn}}\) denotes the (chemical) synaptic input currents entering the cell, \(I_{\text {gap}}\) denotes gap junction input currents and \(I_{\text {ext}}\) are any external currents. For the moment, we ignore the external currents.
The membrane current is modeled by Ohm’s Law and determined by the term \(I_{\text {con}}\)=\(\sum _{k} g_k(V-~E_{k})\), where each k determines a specific ion diffusing through channels in the cell membrane, and \(g_k\) and \(E_k\) determine the gating dynamics and reversal potential of the kth channel, respectively.
We assume that the net chemical synaptic input into neuron i from a population of neurons is determined by \(I_{\text {syn}}= \sum _j \sum _m g_{j}(t-T^m_j)(V_{\text {syn}}-V(t))\), where \(g_{j}\) represents the synaptic dynamics determined by presynaptic neuron j, \(V_{\text {syn}}\) is the synaptic reversal potential, and \(T^m_j\) determines a distribution of firing times of neuron j. Here, we consider no synaptic depression and ignore dendritic architecture. Also, we assume that the chemical synaptic inputs sum linearly.
Gap junctions allow direct diffusion of ions and small molecules between adjacent cells (Goodenough and Paul 2009). Therefore, we assume that the gap junctions are also modeled by Ohm’s Law in a diffusive manner \(I_{\text {gap}}=\sum _j \frac{1}{R} (V_j-V_i)\) where R is the resistance.
Therefore, we obtain from (17):
We observe that the term \(I_{\text {gap}}\) resembles the discretization of a one-dimensional second spatial derivative (similar to Steyn-Ross et al. 2007). That is, considering three aligned neurons \(j-1\), j and \(j+1\), the input from gap junction coupling on cell j is
Without the inclusion of gap junctions, (18) can be further reduced. This is done by considering a temporal averaging of (18) to obtain a closed system of integral equations to later reduce to Wilson–Cowan or Amari-type equations (Ermentrout 1998; Bressloff 2012). The potential \(V_i\) can be considered to be converted into a firing rate by means of a nonlinear function. This can help to establish the potential in a network of neurons as a set of Volterra equations that can be further reduced into the voltage-based model (20). In this reduction, the variable \(u_e\) now accounts for a mean variable denoting the activity of a neuronal population. We note that model (20) does not include action potentials. For this reduction to happen, it is necessary to include the assumption of a slowly acting synaptic current. However, we have mentioned that gap junctions are faster-acting than chemical synaptic current, so this assumption is not valid for gap junctions. We suggest that this may be rectified by considering instead an anomalous diffusion. As a step in this direction, we propose a simple model considering an excitatory and inhibitory population, together with both chemical and electrical synapses, where the electrical synapses are modeled by simple diffusion:
In this model, there is no dynamic component for the gap junction coupling and architecture of the gap junction distribution is not considered. However, we propose that this model is of interest for determining if wave propagation as observed in vivo preceding seizure termination is possible under a simple scenario. This could provide a useful foundation for developing more realistic models including gap junction coupling that mimic wave features observed in vivo.
B Appendix: Traveling wave solutions
We now provide a sketch of the derivation of the traveling wave solutions (3) and (4). We first consider system (1) in moving frame (z, t) where \(z=x-ct\). We look for stationary solutions of this system such that \(\frac{\partial u_j}{\partial t}(z,t)=0\), implying \(u_j(z,t)=u_j(z)\) where \(j=\{e,i\}\). We derive a Green’s function (Stakgold and Holst 2011; Evans 2010) that helps solve the inhomogeneous differential system that arises. The Green’s function that we derive has the following form:
where \(r_1=\frac{-c+\sqrt{c^2+4 \alpha _j D_j^2}}{2 D_j^2}\), and \(r_2=\frac{-c-\sqrt{c^2+4 \alpha _j D_j^2}}{2 D_j^2}\). This Green’s function solves the inhomogeneous system by considering:
where \(g_{jk}=\frac{1}{2\sigma _{jk}}\exp {\left( -\frac{\mid x \mid }{\sigma _{jk}}\right) }\) and H is the Heaviside function. Assuming \(u_j(y)>k_j\) for \(w_{j0}<y<w_{jf}\) we obtain:
Assuming \(w_{i0}\le w_{e0} \le w_{if} \le w_{ef}\) and substituting (21) and (24) into (2223) we obtain the traveling wave solutions (3) and (4):
where
Rights and permissions
About this article
Cite this article
González-Ramírez, L.R., Mauro, A.J. Investigating the role of gap junctions in seizure wave propagation. Biol Cybern 113, 561–577 (2019). https://doi.org/10.1007/s00422-019-00809-6
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00422-019-00809-6