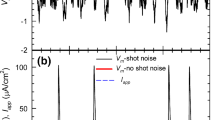
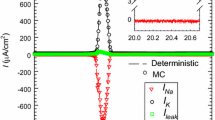
Abstract
Molecular fluctuations can lead to macroscopically observable effects. The random gating of ion channels in the membrane of a nerve cell provides an important example. The contributions of independent noise sources to the variability of action potential timing have not previously been studied at the level of molecular transitions within a conductance-based model ion-state graph. Here we study a stochastic Langevin model for the Hodgkin–Huxley (HH) system based on a detailed representation of the underlying channel state Markov process, the “\(14\times 28\)D model” introduced in (Pu and Thomas in Neural Computation 32(10):1775–1835, 2020). We show how to resolve the individual contributions that each transition in the ion channel graph makes to the variance of the interspike interval (ISI). We extend the mean return time (MRT) phase reduction developed in (Cao et al. in SIAM J Appl Math 80(1):422–447, 2020) to the second moment of the return time from an MRT isochron to itself. Because fixed-voltage spike detection triggers do not correspond to MRT isochrons, the inter-phase interval (IPI) variance only approximates the ISI variance. We find the IPI variance and ISI variance agree to within a few percent when both can be computed. Moreover, we prove rigorously, and show numerically, that our expression for the IPI variance is accurate in the small noise (large system size) regime; our theory is exact in the limit of small noise. By selectively including the noise associated with only those few transitions responsible for most of the ISI variance, our analysis extends the stochastic shielding (SS) paradigm (Schmandt and Galán in Phys Rev Lett 109(11):118101, 2012) from the stationary voltage clamp case to the current clamp case. We show numerically that the SS approximation has a high degree of accuracy even for larger, physiologically relevant noise levels. Finally, we demonstrate that the ISI variance is not an unambiguously defined quantity, but depends on the choice of voltage level set as the spike detection threshold. We find a small but significant increase in ISI variance, the higher the spike detection voltage, both for simulated stochastic HH data and for voltage traces recorded in in vitro experiments. In contrast, the IPI variance is invariant with respect to the choice of isochron used as a trigger for counting “spikes.”














Similar content being viewed by others
Change history
24 June 2021
A Correction to this paper has been published: https://doi.org/10.1007/s00422-021-00882-w
Notes
Equivalently, “iso-phase-intervals”: the time taken to complete one full oscillation, from a given isochron back to the same isochron.
For the \(14\times 28\)D Langevin Hodgkin–Huxley model, \(\varOmega \) may be thought of as the space of continuous vector functions on \([0,\infty )\) with 28 components – one for each independent noise source.
In this paper, we focus on a Langevin equation, rather than models with discrete channel noise. Therefore, our trajectories are diffusions that have continuous sample paths (with probability one). Therefore, the FPT \(\tau ({\mathbf {x}},{\mathcal {S}})\) is well defined. For discrete channel noise models, a slightly modified definition would be required.
(Gardiner 2004), §6.6, First Exit Time from a Region (Homogeneous Processes), equation 6.6.8.
(Gardiner 2004), Chapter 6.6, First Exit Time from a Region (Homogeneous Processes), equation 6.6.11.
Throughout this section, we use the term “threshold” in the data analysis sense of a Schmitt trigger (Schmitt 1938), rather than the physiological sense of a spike generation mechanism.
Note that the factor b, representing the shift in mean frequency due to noise, does not appear in the expression for the variance of the phase after one period. Similarly, the term \({\overline{T}}_1\) appearing in our assumption A3, Eq. (38), represents the first-order shift in mean period of the stochastic oscillator upon introducing nonzero noise. Observe that \({\overline{T}}_1\) does not appear in our expression for the inter-phase interval variance, consistent with the results in Giacomin et al. (2018).
References
Aminzare Z, Holmes P, Srivastava V (2019) On phase reduction and time period of noisy oscillators. In: 2019 IEEE 58th conference on decision and control (CDC), pp 4717–4722
Anderson DF, Ermentrout B, Thomas PJ (2015) Stochastic representations of ion channel kinetics and exact stochastic simulation of neuronal dynamics. J Comput Neurosci 38(1):67–82. https://doi.org/10.1007/s10827-014-0528-2
Azouz R, Gray CM (2000) Dynamic spike threshold reveals a mechanism for synaptic coincidence detection in cortical neurons in vivo. Proc Natl Acad Sci 97(14):8110–8115
Bezanilla F (1987) Single sodium channels from the squid giant axon. Biophys J 52(6):1087–1090
Bressloff PC, Newby JM (2014) Path integrals and large deviations in stochastic hybrid systems. Phys Rev E 89(4):042701
Brown E, Moehlis J, Holmes P (2004) On the phase reduction and response dynamics of neural oscillator populations. Neural Comput 16(4):673–715. https://doi.org/10.1162/089976604322860668
Brunel N, Latham PE (2003) Firing rate of the noisy quadratic integrate-and-fire neuron. Neural Comput 15(10):2281–2306
Buckwar E, Riedler MG (2011) An exact stochastic hybrid model of excitable membranes including spatio-temporal evolution. J Math Biol 63(6):1051–1093
Butera RJ Jr, Rinzel J, Smith JC (1999) Models of respiratory rhythm generation in the pre-Bötzinger complex. I. Bursting pacemaker neurons. J Neurophysiol 82(1):382–397
Cao A (2017) Dimension reduction for stochastic oscillators: investigating competing generalizations of phase and isochrons. Master’s thesis, Case Western Reserve University, Cleveland, Ohio
Cao A, Lindner B, Thomas PJ (2020) A partial differential equation for the mean-return-time phase of planar stochastic oscillators. SIAM J Appl Math 80(1):422–447
Chacron MJ, Lindner B, Longtin A (2004) Noise shaping by interval correlations increases information transfer. Phys Rev Lett 92(8):080601
Dorval AD, White JA (2005) Channel noise is essential for perithreshold oscillations in entorhinal stellate neurons. J Neurosci 25(43):10025–10028
Ermentrout GB, Beverlin B 2nd, Troyer T, Netoff TI (2011) The variance of phase-resetting curves. J Comput Neurosci. https://doi.org/10.1007/s10827-010-0305-9
Ermentrout GB, Terman DH (2010) Foundations of mathematical neuroscience. Springer, Berlin
Faisal AA, White JA, Laughlin SB (2005) Ion-channel noise places limits on the miniaturization of the brain’s wiring. Curr Biol 15(12):1143–1149
Fenwick EM, Marty A, Neher E (1982) Sodium and calcium channels in bovine chromaffin cells. J Physiol 331(1):599–635
Fisch K, Schwalger T, Lindner B, Herz AV, Benda J (2012) Channel noise from both slow adaptation currents and fast currents is required to explain spike-response variability in a sensory neuron. J Neurosci 32(48):17332–17344
Forrest MD (2015) Simulation of alcohol action upon a detailed Purkinje neuron model and a simpler surrogate model that runs\(>\)400 times faster. BMC Neurosci 16(1):27
Fox Lu (1994) Emergent collective behavior in large numbers of globally coupled independently stochastic ion channels. Phys Rev E Stat Phys Plasmas Fluids Relat Interdiscip Topics 49(4):3421–3431
Gardiner CW (2004) Handbook of stochastic methods for physics, chemistry, and the natural sciences, 2nd edn. Springer, Berlin
Gerstein GL (1960) Analysis of firing patterns in single neurons. Science 131(3416):1811–1812
Gerstner W, Kempter R, Van Hemmen JL, Wagner H (1996) A neuronal learning rule for sub-millisecond temporal coding. Nature 383(6595):76–78
Giacomin G, Poquet C, Shapira A (2018) Small noise and long time phase diffusion in stochastic limit cycle oscillators. J Differ Equ 264(2):1019–1049
Goldwyn JH, Shea-Brown E (2011) The what and where of adding channel noise to the Hodgkin–Huxley equations. PLoS Comput Biol 7(11):e1002247. https://doi.org/10.1371/journal.pcbi.1002247
Goldwyn JH, Shea-Brown E, Rubinstein JT (2010) Encoding and decoding amplitude-modulated cochlear implant stimuli: a point process analysis. J Comput Neurosci 28(3):405–424
Guckenheimer J (1975) Isochrons and phaseless sets. J Math Biol 1:259–273. https://doi.org/10.1007/BF01273747
Guckenheimer J, Holmes P (1990) Nonlinear oscillations, dynamical systems, and bifurcations of vector fields. Applied Mathematical Sciences, vol. 42, third edn. Springer
Gutkin BS, Ermentrout GB (1998) Dynamics of membrane excitability determine interspike interval variability: a link between spike generation mechanisms and cortical spike train statistics. Neural Comput 10(5):1047–1065
Kuramoto Y (1984) Chemical Oscillations, Waves, and Turbulence, Springer-Verlag, Berlin
Kurtz TG (1978) Strong approximation theorems for density dependent Markov chains. Stoch Process Appl 6(3):223–240
Lasota A, Mackey MC (1994) Chaos, fractals, and noise: stochastic aspects of dynamics, applied mathematical sciences, vol 97. Springer, New York
Linaro D, Storace M, Giugliano M (2011) Accurate and fast simulation of channel noise in conductance-based model neurons by diffusion approximation. PLoS Comput Biol 7(3):e1001102
Lindner B (2004) Interspike interval statistics of neurons driven by colored noise. Phys Rev E 69(2):022901
Lindner B, Chacron MJ, Longtin A (2005) Integrate-and-fire neurons with threshold noise: a tractable model of how interspike interval correlations affect neuronal signal transmission. Phys Rev E 72(2):021911
Llinás R, Sugimori M (1980) Electrophysiological properties of in vitro Purkinje cell dendrites in mammalian cerebellar slices. J Physiol 305(1):197–213
Llinás R, Sugimori M (1980) Electrophysiological properties of in vitro Purkinje cell somata in mammalian cerebellar slices. J Physiol 305(1):171–195
Mainen ZF, Sejnowski TJ (1995) Reliability of spike timing in neocortical neurons. Science 268(5216):1503–1506
Makielski JC, Sheets MF, Hanck DA, January CT, Fozzard HA (1987) Sodium current in voltage clamped internally perfused canine cardiac Purkinje cells. Biophys J 52(1):1–11
McKane AJ, Newman TJ (2005) Predator-prey cycles from resonant amplification of demographic stochasticity. Phys Rev Lett 94(21):218102
Moiseff A, Konishi M (1981) The owl’s interaural pathway is not involved in sound localization. J Comput Physiol 144(3):299–304
Mukhametov L, Rizzolatti G, Tradardi V (1970) Spontaneous activity of neurones of nucleus reticularis thalami in freely moving cats. J Physiol 210(3):651–667
Neher E, Sakmann B (1976) Single-channel currents recorded from membrane of denervated frog muscle fibres. Nature 260(5554):799
Netoff T, Schwemmer MA, Lewis TJ (2012) Experimentally estimating phase response curves of neurons: theoretical and practical issues. In: Phase Response curves in neuroscience, pp 95–129. Springer
Øksendal B (2007) Stochastic differential equations: an introduction with applications, 6th edn. Springer, Berlin
Orio P, Soudry D (2012) Simple, fast and accurate implementation of the diffusion approximation algorithm for stochastic ion channels with multiple states. PLoS ONE 7(5):e36670
Ovsepian SV, Friel DD (2008) The leaner P/Q-type calcium channel mutation renders cerebellar Purkinje neurons hyper-excitable and eliminates Ca\(^{2+}\)-Na\(^+\) spike bursts. Eur J Neurosci 27(1):93–103
Pakdaman K, Thieullen M, Wainrib G (2010) Fluid limit theorems for stochastic hybrid systems with application to neuron models. Adv Appl Probab 42(3):761–794
Pezo D, Soudry D, Orio P (2014) Diffusion approximation-based simulation of stochastic ion channels: which method to use? Front Comput Neurosci 8:139
Pietrobon D (2010) Ca v 2.1 channelopathies. Pflügers Archiv-Eur J Physiol 460(2):375–393
Pikovsky A (2015) Comment on “asymptotic phase for stochastic oscillators.” Phys. Rev. Lett. 115:069401. https://doi.org/10.1103/PhysRevLett.115.069401
Pu S (2020) Noise decomposition for stochastic Hodgkin-Huxley models. Ph.D. thesis, Case Western Reserve University, Cleveland, Ohio
Pu S, Thomas PJ (2020) Fast and accurate Langevin simulations of stochastic Hodgkin–Huxley dynamics. Neural Comput 32(10):1775–1835
Rajakulendran S, Kaski D, Hanna MG (2012) Neuronal P/Q-type calcium channel dysfunction in inherited disorders of the CNS. Nat Rev Neurol 8(2):86
Risken H (1996) The Fokker–Planck equation: methods of solution and applications, 2nd edn. Springer Series in Synergistics. Springer, Berlin
Rowat P (2007) Interspike interval statistics in the stochastic Hodgkin-Huxley model: coexistence of gamma frequency bursts and highly irregular firing. Neural Comput 19(5):1215–1250
Rowat PF, Greenwood PE (2011) Identification and continuity of the distributions of burst-length and interspike intervals in the stochastic Morris-Lecar neuron. Neural Comput 23(12):3094–3124
Saks S (1937) Theory of the integral. http://eudml.org/doc/219302
Schleimer JH (2013) Spike statistics and coding properties of phase models. Ph.D. thesis, Humboldt-Universität zu Berlin, Mathematisch-Naturwissenschaftliche Fakultät I
Schmandt NT, Galán RF (2012) Stochastic-shielding approximation of Markov chains and its application to efficiently simulate random ion-channel gating. Phys Rev Lett 109(11):118101
Schmid G, Goychuk I, Hänggi P (2001) Stochastic resonance as a collective property of ion channel assemblies. Europhys Lett 56(1):22
Schmidt DR, Galán RF, Thomas PJ (2018) Stochastic shielding and edge importance for Markov chains with timescale separation. PLoS Comput Biol 14(6):e1006206
Schmidt DR, Thomas PJ (2014) Measuring edge importance: a quantitative analysis of the stochastic shielding approximation for random processes on graphs. J Math Neurosci 4(1):6
Schmitt OH (1938) A thermionic trigger. J Sci Instrum 15(1):24
Schneidman E, Freedman B, Segev I (1998) Ion channel stochasticity may be critical in determining the reliability and precision of spike timing. Neural Comput 10(7):1679–1703
Schwabedal J, Pikovsky A (2010) Effective phase dynamics of noise-induced oscillations in excitable systems. Phys Rev E: Stat Nonlinear Soft Matter Phys 81(4 Pt 2):046218
Schwabedal J, Pikovsky A (2013) Phase description of stochastic oscillations. Phys Rev Lett 110:4102
Schwalger T, Fisch K, Benda J, Lindner B (2010) How noisy adaptation of neurons shapes interspike interval histograms and correlations. PLoS Comput Biol 6(12):e1001026
Schwalger T, Tiana-Alsina J, Torrent M, Garcia-Ojalvo J, Lindner B (2012) Interspike-interval correlations induced by two-state switching in an excitable system. Europhys Lett 99(1):10004
Schwemmer MA, Lewis TJ (2012) The theory of weakly coupled oscillators. In: Phase response curves in neuroscience, pp 3–31. Springer
Shadlen MN, Newsome WT (1998) The variable discharge of cortical neurons: implications for connectivity, computation, and information coding. J Neurosci 18(10):3870–3896
Shiau L, Schwalger T, Lindner B (2015) Interspike interval correlation in a stochastic exponential integrate-and-fire model with subthreshold and spike-triggered adaptation. J Comput Neurosci 38(3):589–600
Shingai R, Quandt FN (1986) Single inward rectifier channels in horizontal cells. Brain Res 369(1–2):65–74
Sigworth F (1977) Sodium channels in nerve apparently have two conductance states. Nature 270(5634):265–267
Stein RB (1965) A theoretical analysis of neuronal variability. Biophys J 5(2):173–194
T O’Connor D, Mahata SK, Mahata M, Jiang Q, Hook VY, Taupenot L (2007) Primary culture of bovine chromaffin cells. Nat Protoc 2(5):1248–1253
Thomas PJ, Lindner B (2014) Asymptotic phase for stochastic oscillators. Phys Rev Lett 113(25):254101
Thomas PJ, Lindner B (2015) Thomas and lindner reply. Phys. Rev. Lett. 115.6 (2015): 069402. (A reply to “Comment on Asymptotic Phase for Stochastic Oscillators” by A. Pikovsky, same journal.)
Thomas PJ, Lindner B (2019) Phase descriptions of a multidimensional Ornstein-Uhlenbeck process. Phys Rev E 99(6):062221
Vilela RD, Lindner B (2009) Are the input parameters of white noise driven integrate and fire neurons uniquely determined by rate and CV? J Theor Biol 257(1):90–99
Walter JT, Alvina K, Womack MD, Chevez C, Khodakhah K (2006) Decreases in the precision of Purkinje cell pacemaking cause cerebellar dysfunction and ataxia. Nat Neurosci 9(3):389–397
White JA, Rubinstein JT, Kay AR (2000) Channel noise in neurons. Trends Neurosci 23(3):131–137
Wilson D, Ermentrout B (2018) Greater accuracy and broadened applicability of phase reduction using isostable coordinates. J Math Biol 76(1–2):37–66
Wilson D, Ermentrout B (2018) An operational definition of phase characterizes the transient response of perturbed limit cycle oscillators. SIAM J Appl Dyn Syst 17(4):2516–2543
Wilson D, Ermentrout B (2019) Augmented phase reduction of (not so) weakly perturbed coupled oscillators. SIAM Rev 61(2):277–315
Winfree A (2000) The geometry of biological time, 2nd edn. Springer, New York
Winfree AT (1974) Patterns of phase compromise in biological cycles. J Math Biol 1:73–95
Acknowledgements
The authors thank Dr. David Friel (Case Western Reserve University, School of Medicine) for introducing us to the problem of channel noise and spontaneous spike time variability in the leaner mouse, for providing access to voltage recordings obtained in his laboratory and for many illuminating discussions on mechanisms at work in Purkinje cells. The authors thank Dr. Daniela Calvetti and Dr. Erkki Somersalo (Case Western Reserve University, Department of Mathematics, Applied Mathematics and Statistics) for helpful advice and discussion. This work was made possible in part by grants from the National Science Foundation (DMS-2052109, DEB-1654989). PT thanks the Oberlin College Department of Mathematics for research support. This research has been supported in part by the Mathematical Biosciences Institute and the National Science Foundation under grant DMS-1440386. Large-scale simulations made use of the High Performance Computing Resource in the Core Facility for Advanced Research Computing at Case Western Reserve University.
Author information
Authors and Affiliations
Corresponding author
Additional information
Communicated by André Longtin.
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
The original article has been updated: Due to textual changes.
Appendices
Model parameters, common symbols and notations
Subunit kinetics for Hodgkin and Huxley parameters are given by
where the diagonal elements
Diffusion matrix of the 14D model
Define the state vector for \(\hbox {Na}^+\) and \(\hbox {K}^+\) channels as
and \({\mathbf {N}}=[n_0,n_1,n_2,n_3,n_4]^\intercal \), respectively.
The matrices \(S_\text {K}\) and \(S_\text {Na}\) are given by

and

where \(S^{(i:j)}_\text {Na}\) is the \(\hbox {i}^{th}\)-\(\hbox {j}^{th}\) column of \(S_\text {Na}\).
Note that each of the 8 columns of \(S_\text {K}\) corresponds to the flux vector along a single directed edge in the \(\hbox {K}^+\) channel transition graph. Similarly, each of the 20 columns of \(S_\text {Na}\) corresponds to the flux vector along a directed edge in the \(\hbox {Na}^+\) graph (cf. Fig. 2). Factors \(M_\text {ref}=6000\) and \(N_\text {ref}=1800\) represent the reference number of \(\hbox {K}^+\) and \(\hbox {Na}^+\) channels from Goldwyn and Shea-Brown’s model (Goldwyn and Shea-Brown 2011).
Proof of Lemma 1
For the reader’s convenience, we restate
Lemma 1For a conductance-based model of the form (3), and for any fixed applied current \(I_\text {app}\), there exist upper and lower bounds \(v_\text {max}\) and \(v_\text {min}\) such that trajectories with initial voltage condition \(v\in [v_\mathrm{min},v_\mathrm{max}]\) remain within this interval for all times \(t>0\), with probability 1, regardless of the initial channel state, provided the gating variables satisfy \(0\le M_{ij}\le 1\) and \(0\le N_i\le 1\).
Proof
Let \(V_1={\text {min}}_{\mathrm{ion}}\{V_\mathrm{ion}\}\wedge V_\mathrm{leak}\), and \(V_2={\text {max}}_{\mathrm{ion}}\{V_\mathrm{ion}\}\vee V_\mathrm{leak}\), where \(\text {ion}\in \{\text {Na}^+, \text {K}^+\}\). Note that by assumption, for both the \(\hbox {Na}^+\) and \(\hbox {K}^+\) channel, \(0\le {M_{31}} \le 1\), \(0\le {N_4} \le 1\). Moreover, \(g_i>0,\ g_\mathrm{leak}>0\); therefore, when \(V\le V_1\)
Inequality (115) holds with probability 1 because \(V_1 ={\text {min}}_{i\in {\mathcal {I}}} \wedge V_\text {leak}\), and inequality (116) follows because \(V-V_1\le 0\), \(g_i>0\) and \({M_{31}}\ge 0\), \({N_4}\ge 0\). Let \(V_\text {min}:=\text {min}\left\{ \frac{I_-}{g_\text {leak}} +V_1,V_1\right\} \). When \(V<V_\text {min}\), \(\frac{\hbox {d}V}{\hbox {d}t}>0\). Therefore, V will not decrease beyond \(V_\text {min}\).
Similarly, when \(V\ge V_2\)
Inequality (119) and inequality (120) hold because \(V_2={\text {max}}_{i\in {\mathcal {I}}}\{V_i\}\vee V_\text {leak},\) \(V-V_2\ge 0\), \(g_i>0\) and \({M_{31}}\ge 0\), \({N_4}\ge 0\). Let \(V_\text {max}=\text {max}\left\{ \frac{I_\text {app}}{g_\text {leak}}+V_2, V_2 \right\} \). When \(V>V_\text {max},\) \(\frac{\hbox {d}V}{\hbox {d}t}<0\). Therefore, V will not go beyond \(V_\text {max}\).
We conclude that if V takes an initial condition in the interval \([V_\text {min},V_\text {max}],\) and if \(0\le M_{ij},N_i\le 1\) for all time, then V(t) remains within this interval for all \(t\ge 0\). Thus, we complete the proof of Lemma 1. \(\square \)
Experimental methods
Whole-cell current clamp recordings of Purkinje cells from in vitro cerebellar slice preparations taken from wild type and leaner mice were performed in the laboratory of Dr. David Friel (Case Western Reserve University School of Medicine), as described in Ovsepian and Friel (2008). Experimental procedures conformed to guidelines approved by the Institutional Animal Care and Use Committee at Case Western Reserve University. Voltage signals were sampled at a frequency of 20kHz, filtered at 5–10 kHz, digitized at a resolution of 32/mV and analyzed using custom software written in IgorPro and MATLAB.
Comparison of our main theorem with the related literature
1.1 Comparison with Giacomin et al. (2018)
Giacomin et al. (2018) considered a one-parameter family of strong solutions of the (Ito) stochastic differential equation
where the parameter \(\varepsilon > 0\), \(F(\cdot )\) is a locally Lipschitz vector field on \({\mathbb {R}}^d\), \(G(\cdot )\) is a locally Lipschitz function on \({\mathbb {R}}^d\) with values in the \(d\times m\) matrices and \(B_\cdot \) is a standard m dimensional Brownian motion. Note that in our formulation of the Langevin system (3), we use \(\sqrt{\epsilon }\) where Giacomin et al. use \(\varepsilon \). Consequently, our expressions involving \(GG^\intercal \) scale as \(\epsilon \), whereas the analogous expressions scale as \(\varepsilon ^2\) in Giacomin et al. (2018).
If the deterministic asymptotic phase is \(\theta (x)\), then evaluated along a trajectory \(\theta (X^\varepsilon _t)\) the phase obeys Ito’s formula:
where \({\mathcal {D}}=GG^\intercal \) and we use Einstein’s summation convention. Given their definition of the asymptotic phase function and their Theorem 2.1 on page 1024, \(F_i(x)\partial _i\theta (x)=1\). As a result of their Theorem 2.3 (page 1026 in Giacomin et al. 2018), if \(\varepsilon \) is small, then over long times, we can establish that (since \(X^\varepsilon _t\) stays “close to” the deterministic limit cycle solution \(q_t=X^0_t\) for times on the order of \(t/\varepsilon ^2\)) approximately
for some constants \(\sigma \) and b that one may calculate in terms of F and G for any particular system. The notation \({\tilde{\theta }}\) refers to the “lift” of \(\theta \) from the circle \(\theta \in {\mathbb {S}}_T\equiv [0,T)\) to \({\tilde{\theta }}\in {\mathbb {R}}\), i.e., the integral of (124) without the jumps induced by taking \(\theta \) mod the period T. For small noise \(\varepsilon \), integrating up to time t, we have (provided t is \(o(\varepsilon ^{-2})\), and setting \(x_0\equiv X_0^\varepsilon \)),
where \(W_t\) is now a 1D standard Brownian motion (with \(\approx \) signifying convergence in distribution, after rescaling time). Upon rescaling time, the authors establish that
Therefore, the accumulated variance of \({\tilde{\theta }}(X^\varepsilon _t)\) during one (deterministic) period T is
Equation (128) holds because the variance of the Wiener process increment over time T is exactly T and because the limit cycle period T is a deterministic quantity.Footnote 7 Equation (129) holds by virtue of the authors’ formula, Eq. (2.20) on page 1026 in Giacomin et al. (2018).
Finally, we note that, for a conductance-based channel noise model of the type we consider in this paper, the expression \(D\theta (q_s)G(q_s)G^t(q_s)D\theta ^t(q_s)\) in Giacomin et al. (2018) corresponds exactly with our expression \(\sum _{ij}({\mathcal {G}}{\mathcal {G}}^\intercal )_{ij}\partial _{i}T_0\partial _{j}T_0\) and \(\sum _{k=1}^{28}\alpha _k(v){\mathbf {X}}_{i(k)} \left( \zeta _k^\intercal {\tilde{{\mathbf {Z}}}}\right) ^2,\) as in our Theorem 1 and Corollary 1. To see the correspondence, note that \(D\theta (q_s)\), the gradient of the phase function evaluated along the limit cycle is none other than the infinitesimal phase response curve and is identical to the gradient of the zero-noise timing function \(\nabla T_0\); the rest follows from the structure of \({\mathcal {G}}\) as shown in the proof of our main theorem.
1.2 Comparison with Aminzare et al. (2019)
In Aminzare et al. (2019), the authors consider the scaled Langevin model (Eq. (10) on page 4718)
The authors consider the special case in which \(B(x)=\text {diag}(\beta _1,\ldots ,\beta _n)\). Our corresponding matrix \({\mathcal {G}}\) is not diagonal, due to the biophysical origin of channel noise, so direct comparison of our results is somewhat limited. Nevertheless, the authors consider the moments of the stochastic period, defined as the time to complete one oscillation, and arrive at an expression for the variance of the stochastic period that we can compare with the result of our theorem 1. In particular, in Proposition 3 on page 4721 in Aminzare et al. (2019), the authors calculate the first and second moments of the stochastic return time T for system (130) with \(B(x)=\text {diag}(\beta _1,\ldots ,\beta _n)\) as
and
where
\(H(\theta )\) is the “second-order” PRC (the Hessian of the asymptotic phase function) and \(Z(\theta )\) is the infinitesimal phase response curve. Note that because (Aminzare et al. 2019) scales phase from 0 to \(2\pi \), their expression \(\zeta (\theta _0)\) has units of radians/time. In contrast, our infinitesimal phase response curve \({\mathbf {Z}}(t)\) has units of time; we may convert by multiplying by \(T_0/2\pi \) (Sect. 2.4). Although \({\mathcal {G}}\) is not diagonal for conductance-based neural oscillators driven by channel noise (cf. Eq. (3)), we can still express the term \(\zeta (\theta _0)\) as
Given the first and second moments of the time period in Aminzare et al. (2019), the variance is given by
By Tonelli’s Theorem (Saks 1937),
Therefore, Eq. (138) reduces to
which is consistent with our main result, because \(\sigma ^2=\epsilon \), \(\omega =2\pi /T\), and \(\hbox {d}\alpha \sim \omega \,\hbox {d}t\).
Rights and permissions
About this article
Cite this article
Pu, S., Thomas, P.J. Resolving molecular contributions of ion channel noise to interspike interval variability through stochastic shielding. Biol Cybern 115, 267–302 (2021). https://doi.org/10.1007/s00422-021-00877-7
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00422-021-00877-7