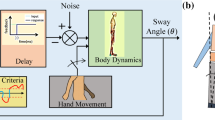
Abstract
Maintaining balance is an essential skill regulated by the central nervous system (CNS) that helps humans to function effectively. Developing a physiologically motivated computational model of a neural controller with good performance is a central component for a large range of potential applications, such as the development of therapeutic and assistive devices, diagnosis of balance disorders, and designing robotic control systems. In this paper, we characterize the biomechanics of postural control system by considering the musculoskeletal dynamics in the sagittal plane, proprioceptive feedback, and a neural controller. The model includes several physiological structures, such as the feedforward and feedback mechanism, sensory noise, and proprioceptive feedback delays. A high-gain observer (HGO)-based feedback linearization controller represents the CNS analog in the modeling paradigm. The HGO gives an estimation of delayed states and the feedback linearization control law generates the feedback torques at joints to execute postural recovery movements. The whole scheme is simulated in MATLAB/Simulink. The simulation results show that our proposed scheme is robust against larger perturbations, sensory noises, feedback delays and retains a strong disturbance rejection and trajectory tracking capability. Overall, these results demonstrate that the nonlinear system dynamics, the feedforward and feedback mechanism, and physiological latencies play a key role in shaping the motor control process.







Similar content being viewed by others
References
Alexandrov AV, Frolov AA, Horak F, Carlson-Kuhta P, Park S (2005) Feedback equilibrium control during human standing. Biol Cybern 93(5):309–322. https://doi.org/10.1007/s00422-005-0004-1
Barin K (1989) Evaluation of a generalized model of human postural dynamics and control in the sagittal plane. Biol Cybern 61(1):37–50. https://doi.org/10.1007/BF00204758
Chiba R, Takakusaki K, Ota J, Yozu A, Haga N (2016) Human upright posture control models based on multisensory inputs; in fast and slow dynamics. Neurosci Res 104:96–104. https://doi.org/10.1016/j.neures.2015.12.002
Coelho DB, Duarte M (2014) Human postural control during standing posture with a muscle-tendon actuator. Int J Exp Comput Biomech 2(4):343–358. https://doi.org/10.1504/IJECB.2014.066090
Doyle JC, Glover K, Khargonekar PP, Francis BA (1989) State-space solutions to standard H/sub 2/and H/sub infinity/control problems. IEEE Trans Autom Control 34(8):831–847. https://doi.org/10.1109/9.29425
Hwang S, Tae K, Sohn R, Kim J, Son J, Kim Y (2009) The balance recovery mechanisms against unexpected forward perturbation. Ann Biomed Eng 37(8):1629–1637. https://doi.org/10.1007/s10439-009-9717-y
Iqbal J, Ullah M, Khan SG, Khelifa B, Ćuković S (2017) Nonlinear control systems-A brief overview of historical and recent advances. Nonlinear Eng 6(4):301–312. https://doi.org/10.1515/nleng-2016-0077
Iqbal K (2020) Optimal time-varying postural control in a single-link neuromechanical model with feedback latencies. Biol Cybern 114(4):485–497. https://doi.org/10.1007/s00422-020-00843-9
Iqbal K, Mughal AM Active control vs. passive stiffness in posture and movement coordination. In: 2007 IEEE International Conference on Systems, Man and Cybernetics, 2007, pp 3367–3372. https://doi.org/10.1109/ICSMC.2007.4414105
Iqbal K, Pai Y-C (2000) Predicted region of stability for balance recovery: motion at the knee joint can improve termination of forward movement. J Biomech 33(12):1619–1627. https://doi.org/10.1016/s0021-9290(00)00129-9
Iqbal K, Roy A (2009) A novel theoretical framework for the dynamic stability analysis, movement control, and trajectory generation in a multisegment biomechanical model. J Biomech Eng. https://doi.org/10.1115/1.3002763
Iqbal K, Roy A (2004) Stabilizing PID controllers for a single-link biomechanical model with position, velocity, and force feedback. J Biomech Eng 126(6):838–843. https://doi.org/10.1115/1.1824134
Ishida A, Imai S, Fukuoka Y (1997) Analysis of the posture control system under fixed and sway-referenced support conditions. IEEE Trans Biomed Eng 44(5):331–336. https://doi.org/10.1109/10.568908
Ivanenko Y, Gurfinkel VS (2018) Human postural control. Front Neurosci 12:171. https://doi.org/10.3389/fnins.2018.00171
Jafari H, Nikolakopoulos G, Gustafsson T Stabilization of an inverted pendulum via human brain inspired controller design. In: 2019 IEEE-RAS 19th International Conference on Humanoid Robots (Humanoids), 2019, pp 433–438. https://doi.org/10.1109/Humanoids43949.2019.9035019
Jeka J, Kiemel T (2009) Modeling of human postural control. In: Encyclopedia of Neuroscience. Springer Berlin Heidelberg, pp 2381–2384. https://doi.org/10.1007/978-3-540-29678-2_3534
Jiang P, Chiba R, Takakusaki K, Ota J (2016) Generation of the human biped stance by a neural controller able to compensate neurological time delay. PLoS ONE 11(9):e0163212. https://doi.org/10.1371/journal.pone.0163212
Khalil HK (2017) High-gain observers in nonlinear feedback control. SIAM. https://doi.org/10.1137/1.9781611974867.ch3
Khalil HK, Grizzle JW (2002) Nonlinear systems, vol 3. Prentice Hall, Upper Saddle River
Kiemel T, Oie KS, Jeka JJ (2002) Multisensory fusion and the stochastic structure of postural sway. Biol Cybern 87(4):262–277. https://doi.org/10.1007/s00422-002-0333-2
Kuo AD (2005) An optimal state estimation model of sensory integration in human postural balance. J Neural Eng 2(3):S235. https://doi.org/10.1088/1741-2560/2/3/S07
Le Mouel C, Brette R (2019) Anticipatory coadaptation of ankle stiffness and sensorimotor gain for standing balance. PLoS Comput Biol 15(11):e1007463. https://doi.org/10.1371/journal.pcbi.1007463
Lei J, Khalil HK (2015) Feedback linearization for nonlinear systems with time-varying input and output delays by using high-gain predictors. IEEE Trans Autom Control 61(8):2262–2268. https://doi.org/10.1109/TAC.2015.2491719
Lei J, Khalil HK (2016a) High-gain-predictor-based output feedback control for time-delay nonlinear systems. Automatica 71:324–333. https://doi.org/10.1016/j.automatica.2016.05.026
Lei J, Khalil HK (2016b) Robustness of high-gain-observer-based controllers to time delays. In: 2016 American Control Conference (ACC). IEEE, pp 967–972. https://doi.org/10.1109/ACC.2016.7525040
Levine WS (1999) Control system fundamentals, 1st edn. CRC Press, Boca Raton. https://doi.org/10.1201/9781315214030
Mergner T, Peterka RJ (2016) Human sense of balance. In: Goswami A, Vadakkepat P (eds) Humanoid robotics: a reference. Springer, Dordrecht, pp 1–38. https://doi.org/10.1007/978-94-007-7194-9_37-1
Mughal A, Iqbal K (2005) A fuzzy biomechanical model for optimal control of sit-to-stand movement. In: 2005 ICSC congress on computational intelligence methods and applications, 2005. IEEE, p 6
Mughal AM (2016) Real time modeling, simulation and control of dynamical systems. Springer, Berlin. https://doi.org/10.1007/978-3-319-33906-1
Mughal AM, Iqbal K Synthesis of angular profiles for bipedal sit-to-stand movement. In: 2008 40th southeastern symposium on system theory (SSST), 2008. IEEE, pp 293–297. https://doi.org/10.1109/SSST.2008.4480240
Mughal AM, Iqbal K (2012) Physiological LQR design for postural control coordination of sit-to-stand movement. Cogn Comput 4(4):549–562. https://doi.org/10.1007/s12559-012-9160-5
Mughal AM, Iqbal K (2019) Optimization of biomechanical sts movement with linear matrix inequalities. Mechatron Syst Control 47:1–11. https://doi.org/10.2316/J.2019.201-2753
Peterka R (2002) Sensorimotor integration in human postural control. J Neurophysiol 88(3):1097–1118. https://doi.org/10.1152/jn.2002.88.3.1097
Peterka RJ (2000) Postural control model interpretation of stabilogram diffusion analysis. Biol Cybern 82(4):335–343. https://doi.org/10.1007/s004220050587
Rasool G, Farooq H, Mughal AM (2010) Biomechanical sit-to-stand movement with physiological feedback latencies. In: International conference on mechanical and electronics engineering, Center for Advanced Studies in Engineering Islamabad, Pakistan, ICMEE, 2010.
Rowland BA, Quessy S, Stanford TR, Stein BE (2007) Multisensory integration shortens physiological response latencies. J Neurosci 27(22):5879–5884. https://doi.org/10.1523/JNEUROSCI.4986-06.2007
Safi K, Mohammed S, Amirat Y, Khalil M Postural stability analysis—a review of techniques and methods for human stability assessment. In: 2017 Fourth international conference on advances in biomedical engineering (ICABME), 2017. IEEE, pp 1–4. https://doi.org/10.1109/ICABME.2017.8167565
Schumacher C, Berry A, Lemus D, Rode C, Seyfarth A, Vallery H (2019) Biarticular muscles are most responsive to upper-body pitch perturbations in human standing. Sci Rep 9(1):1–14. https://doi.org/10.1038/s41598-019-50995-3
Sinkjaer T, Toft E, Andreassen S, Hornemann BC (1988) Muscle stiffness in human ankle dorsiflexors: intrinsic and reflex components. J Neurophysiol 60:1110–1121
Sultan N, Najam ul Islam M, Mahmood Mughal A (2020) Nonlinear robust compensator design for postural control of a biomechanical model with delayed feedback. Meas Control 53(3–4):679–690. https://doi.org/10.1177/0020294019900285
Sultan N, ul Islam MN, Mughal AM (2018) Postural control during standing posture for small perturbations with feedback linearization. In: 2018 18th international conference on mechatronics-mechatronika (ME). IEEE, pp 1–6
Todorov E (2005) Stochastic optimal control and estimation methods adapted to the noise characteristics of the sensorimotor system. Neural Comput 17:1084–1108
Zak SH (2003) Systems and control, vol 198. Oxford University Press, New York. https://doi.org/10.1002/rnc.992
Zhou K, Doyle JC, Glover K (1996) Robust and optimal control, vol 40. Prentice Hall, New Jersey
Funding
This research received no external funding.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflicts of Interest
The authors declare no conflict of interest.
Availability of data and material
Upon request.
Code availability
Upon request.
Additional information
Communicated by Benjamin Lindner.
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendix A
Appendix A
See Table 1.
1.1 Optimal Weights adopted from (Mughal and Iqbal 2012)
\({C}_{y}=\left[\begin{array}{cccccc}26739& 0& 0& 0& 0& 0\\ 0& 25069& 0& 0& 0& 0\\ 0& 0& 71105& 0& 0& 0\\ 0& 0& 0& 45960& 0& 0\\ 0& 0& 0& 0& 41250& 0\\ 0& 0& 0& 0& 0& 89620\end{array}\right]\), \({D}_{yu}=\left[\begin{array}{ccc}2.3045& 0& 0\\ 0& 4.8403& 0\\ 0& 0& 2.7697\end{array}\right]\)
Rights and permissions
About this article
Cite this article
Sultan, N., Najam ul Islam, M. & Mughal, A.M. Nonlinear postural control paradigm for larger perturbations in the presence of neural delays. Biol Cybern 115, 397–414 (2021). https://doi.org/10.1007/s00422-021-00889-3
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00422-021-00889-3