Human motor learning is robust to control-dependent noise

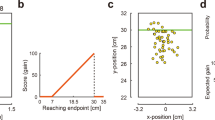
Abstract

Noises are ubiquitous in sensorimotor interactions and contaminate the information provided to the central nervous system (CNS) for motor learning. An interesting question is how the CNS manages motor learning with imprecise information. Integrating ideas from reinforcement learning and adaptive optimal control, this paper develops a novel computational mechanism to explain the robustness of human motor learning to the imprecise information, caused by control-dependent noise that exists inherently in the sensorimotor systems. Starting from an initial admissible control policy, in each learning trial the mechanism collects and uses the noisy sensory data (caused by the control-dependent noise) to form an imprecise evaluation of the performance of the current policy and then constructs an updated policy based on the imprecise evaluation. As the number of learning trials increases, the generated policies mathematically provably converge to a (potentially small) neighborhood of the optimal policy under mild conditions, despite the imprecise information in the learning process. The mechanism directly synthesizes the policies from the sensory data, without identifying an internal forward model. Our preliminary computational results on two classic arm reaching tasks are in line with experimental observations reported in the literature. The model-free control principle proposed in the paper sheds more lights into the inherent robustness of human sensorimotor systems to the imprecise information, especially control-dependent noise, in the CNS.

Appendix A Proof of Theorem 2

Let $\epsilon = \epsilon _1/2$ in Theorem 1. We firstly show that for each stabilizing $\hat{K}_i\in {\mathbb {R}}^{m\times n}$, there exist an integer $N_i$ and a constant $s_i>0$, such that if Assumption 1 is satisfied, then for any $N>N_i$ and $s>s_i$, almost surely

$$\begin{aligned} \Vert \Delta G_i\Vert _F<\delta . \end{aligned}$$

(27)

By definition,

$$\begin{aligned} \begin{aligned} \Vert \Delta G_i\Vert _F&= \Vert G(\hat{P}_i) - \hat{G}_i\Vert _F\le 2\Vert \theta (\hat{P}_i) - \hat{\theta }(\check{P}_i(s))\Vert _F \\&= 2\Vert \theta (\hat{P}_i) - \theta (\check{P}_i(s)) + \theta (\check{P}_i(s)) - \hat{\theta }(\check{P}_i(s))\Vert _F \\&\le 2C_0\Vert \hat{P}_i - \check{P}_i(s) \Vert _F + 2\Vert \theta (\check{P}_i(s)) - \hat{\theta }(\check{P}_i(s)) \Vert _F, \end{aligned} \end{aligned}$$

where $C_0>0$ is a constant. Then, we only need to show that for any $N>N_i$ and $s>s_i$,

$$\begin{aligned} \Vert \hat{P}_i - \check{P}_i(s) \Vert _F< \frac{\delta }{4C_0},\quad \Vert \theta (\check{P}_i(s)) - \hat{\theta }(\check{P}_i(s)) \Vert _F<\frac{\delta }{4}. \end{aligned}$$

Vectorizing (15) yields

$$\begin{aligned} \begin{aligned} \dot{\bar{p}}_i&= {\mathcal {T}}(\varPhi _{i,M,N},\varPsi _{i,M,N},\hat{K}_i) \bar{p}_i \\&\quad + \left[ I_n,-\hat{K}^{\mathrm{T}}_i\right] \otimes \left[ I_n,-\hat{K}^{\mathrm{T}}_i\right] {{\,\mathrm{vec}\,}}(Q\oplus R), \end{aligned} \end{aligned}$$

(28)

where $\bar{p}_i={{\,\mathrm{vec}\,}}(\bar{P}_i)$, i.e., the vectorization of matrix $\bar{P}_i$,

$$\begin{aligned} \begin{aligned}&{\mathcal {T}}(\varPhi _{i,M,N},\varPsi _{i,M,N},\hat{K}_i) \\&= \left[ I_n,-\hat{K}^{\mathrm{T}}_i\right] \otimes \left[ I_n,-\hat{K}^{\mathrm{T}}_i\right] \left( I_{(m+n)^2} -(0_n \oplus I_m) \right. \\&\quad \left. \otimes (0_n \oplus I_m)\right) D_{m+n}\varPhi ^\dagger _{i,M,N}\varPsi _{i,M,N}D_n^\dagger , \end{aligned} \end{aligned}$$

and for $Y\in {\mathbb {S}}^n$, $D_n\in {\mathbb {R}}^{n^2\times \frac{1}{2}n(n+1)}$ is the unique matrix with full column rank (Magnus and Neudecker 2007, Page 57) such that

$$\begin{aligned} {{\,\mathrm{vec}\,}}(Y) = D_n{{\,\mathrm{svec}\,}}(Y),\quad {{\,\mathrm{svec}\,}}(Y) = D_n^\dagger {{\,\mathrm{vec}\,}}(Y). \end{aligned}$$

Vectorizing (18) yields

$$\begin{aligned} \begin{aligned} \dot{\check{p}}_i&= {\mathcal {T}}(\hat{\varPhi }_{i,M,N},\hat{\varPsi }_{i,M,N},\hat{K}_i) \check{p}_i \\&\quad + \left[ I_n,-\hat{K}^{\mathrm{T}}_i\right] \otimes \left[ I_n,-\hat{K}^{\mathrm{T}}_i\right] {{\,\mathrm{vec}\,}}(Q\oplus R), \end{aligned} \end{aligned}$$

(29)

where $\check{p}_i = {{\,\mathrm{vec}\,}}(\check{P}_i)$. Since (8), (9), (28) and (15) are mutually equivalent with Assumption 1, by (17)

$$\begin{aligned} \begin{aligned}&\lim \limits _{N\rightarrow \infty } {\mathcal {T}}(\hat{\varPhi }_{i,M,N},\hat{\varPsi }_{i,M,N},\hat{K}_i)\\&= {\mathcal {T}}(\varPhi _{i,M,N},\varPsi _{i,M,N},\hat{K}_i) \\&= \left( I_n\otimes (A-B\hat{K}_i)^{\mathrm{T}} + (A-B\hat{K}_i)^{\mathrm{T}}\otimes I_n\right) . \end{aligned} \end{aligned}$$

(30)

Since $\hat{K}_i$ is stabilizing, by continuity, there exists an integer $N_{i,1}$, such that for any $N>N_{i,1}$, ${\mathcal {T}}(\hat{\varPhi }_{i,M,N},\hat{\varPsi }_{i,M,N},\hat{K}_i)$ is Hurwitz. Then, we have

$$\begin{aligned} \lim \limits _{t\rightarrow \infty } \bar{P}_i(t) = \hat{P}_i,\qquad \lim \limits _{t\rightarrow \infty } \check{P}_i(t) = \mathring{P}_i, \end{aligned}$$

(31)

where

$$\begin{aligned} \begin{aligned} {{\,\mathrm{vec}\,}}(\hat{P}_i)&= -{\mathcal {T}}^\dagger (\varPhi _{i,M,N},\varPsi _{i,M,N},\hat{K}_i)\\&\quad \left[ I_n,-\hat{K}^{\mathrm{T}}_i\right] \otimes \left[ I_n,-\hat{K}^{\mathrm{T}}_i\right] {{\,\mathrm{vec}\,}}(Q\oplus R),\\ {{\,\mathrm{vec}\,}}(\mathring{P}_i)&= -{\mathcal {T}}^\dagger (\hat{\varPhi }_{i,M,N},\hat{\varPsi }_{i,M,N},\hat{K}_i) \\&\quad \left[ I_n,-\hat{K}^{\mathrm{T}}_i\right] \otimes \left[ I_n,-\hat{K}^{\mathrm{T}}_i\right] {{\,\mathrm{vec}\,}}(Q\oplus R). \end{aligned} \end{aligned}$$

By continuity of matrix inversion, (17) and (31), there exist an integer $N_{i,2}\ge N_{i,1}$ and $s_{i}>0$, such that for any $N>N_{i,2}$ and $s>s_{i}$

$$\begin{aligned} \Vert \hat{P}_i - \check{P}_i(s) \Vert _F \le \Vert \hat{P}_i - \mathring{P}_i\Vert _F + \Vert \mathring{P}_i - \check{P}_i(s) \Vert _F < \frac{\delta }{4C_0}, \end{aligned}$$

and

$$\begin{aligned} \begin{aligned}&\Vert \theta (\check{P}_i(s)) - \hat{\theta }(\check{P}_i(s)) \Vert _F\\&\le \Vert \hat{\varPhi }_{i,M,N}^\dagger \hat{\varPsi }_{i,M,N} - \varPhi _{i,M,N}^\dagger \varPsi _{i,M,N} \Vert _F\Vert \check{P}_i(s)\Vert _F<\frac{\delta }{4}. \end{aligned} \end{aligned}$$

Setting $N_i = N_{i,2}$ completes the proof of (27). By Theorem 1, there exists an integer $\bar{I}$, such that if

$$\begin{aligned} \Vert \Delta G_i\Vert _F<\delta , \qquad i = 1,\ldots , \bar{I}, \end{aligned}$$

(32)

then $\Vert \hat{K}_{\bar{I}} - K^*\Vert _F<\epsilon _1$. Condition (32) can be satisfied by setting

$$\begin{aligned} N_0 = \max (N_1,\ldots , N_{\bar{I}}),\quad s_0 = \max (s_1,\ldots , s_{\bar{I}}). \end{aligned}$$

This completes the proof.