Pulse-frequency-dependent resonance in a population of pyramidal neuron models

Abstract

Stochastic resonance is known as a phenomenon whereby information transmission of weak signal or subthreshold stimuli can be enhanced by additive random noise with a suitable intensity. Another phenomenon induced by applying deterministic pulsatile electric stimuli with a pulse frequency, commonly used for deep brain stimulation (DBS), was also shown to improve signal-to-noise ratio in neuron models. The objective of this study was to test the hypothesis that pulsatile high-frequency stimulation could improve the detection of both sub- and suprathreshold synaptic stimuli by tuning the frequency of the stimulation in a population of pyramidal neuron models. Computer simulations showed that mutual information estimated from a population of neural spike trains displayed a typical resonance curve with a peak value of the pulse frequency at 80–120 Hz, similar to those utilized for DBS in clinical situations. It is concluded that a “pulse-frequency-dependent resonance” (PFDR) can enhance information transmission over a broad range of synaptically connected networks. Since the resonance frequency matches that used clinically, PFDR could contribute to the mechanism of the therapeutic effect of DBS.

Appendix

1.1 Cable equation of pyramidal neuron model

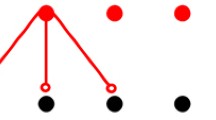
Fig. 1b shows the structure of a single pyramidal neuron model and the corresponding equivalent circuit whose cable equation is expressed as:

$$\begin{aligned}&C_m(x)\frac{\partial V_m(x,t)}{\partial t} + \frac{V_m(x,t)}{R_m(x)} + I_{\mathrm{ion}}(t) { + I_{\mathrm{syn}}(t) } \nonumber \\&\quad = h^2\frac{\partial }{\partial x}\frac{1}{R_a(x)} \left( \frac{\partial V_m(x,t)}{\partial x} + \frac{\partial V_e(x,t)}{\partial x}\right) \end{aligned}$$

(A.1)

where $V_m(t)$, $C_m$, $R_m$, $R_a$, h and $I_{\mathrm{syn}}(t)$ stand for membrane potential, membrane capacitance, membrane resistance, axial resistance, and infinitesimal length, and synaptic input from other neurons, respectively. The extracellular potential $V_e(x,t)$ is represented as

$$\begin{aligned} V_e(x,t)=\frac{\rho _{exp}}{4 \pi z_d} \, I_{\mathrm{pulse}}(t) \end{aligned}$$

(A.2)

where the $\rho _{ext}$, and $z_d$ denote extracellular resistivity, and the distance between the electrode and the fiber at x, respectively. The pulsatile HFS $I_{\mathrm{pulse}}(t)$ is expressed as:

$$\begin{aligned} I_{\mathrm{pulse}}(t) = \left\{ \begin{array}{l} I_{p} \displaystyle \sum _{n=0} \{ u(t- n\tau _{\mathrm{int}}) -2 u(t-w- n\tau _{\mathrm{int}}) \\ ~~~~~~~~+ u(t-2w- n\tau _{\mathrm{int}}) \} \\ ~~~~~~~~~~~~~(n\tau _{\mathrm{int}} \le t < n\tau _{\mathrm{int}}+2w) \\ 0 ~~~~~~~~~~~~(\mathrm{otherwise}) \end{array} \right. \end{aligned}$$

(A.3)

where $I_{p}$ denotes the amplitude of pulsatile stimuli set at 14, 15, or 16 $\mu A$, $w=40$ $\mu s$, and $\tau _{\mathrm{int}}$ denotes the inverse of pulse frequency, and in which u(t) denotes a unit step function as follows:

$$\begin{aligned} u(t) = \left\{ \begin{array}{ll} 1 &{}\quad (0 \le t) \\ 0 &{}\quad (\mathrm{otherwise}) \end{array} \right. . \end{aligned}$$

(A.4)

The extracellular resistivity $\rho _{ext}$ was set at 300.0 $\Omega \cdot$cm. In order to solve (A.1) with numerical calculations, the discretized version of (A.1) is obtained as follows:

$$\begin{aligned}&C_m^{[k]}\frac{V_m^{[i,k]}(t+\varDelta t) - V_m^{[i,k]}(t)}{\varDelta t} + \frac{V_m^{[i,k]}(t)}{R_m^{[i,k]}} + I_{\mathrm{ion}}^{[i,k]}(t) + { I_{\mathrm{syn}}^{[i,k]}(t) } \nonumber \\&\quad = \left( \frac{V_m^{[i,k+1]}(t) - V_m^{[i,k]}(t)}{R_a^{[k+1,k]}} - \frac{V_m^{[i,k]}(t) - V_m^{[i,k-1]}(t)}{R_a^{[k,k-1]}} \right) \nonumber \\&\qquad + \left( \frac{V_e^{[i,k+1]}(t) - V_e^{[i,k]}(t)}{R_a^{[k+1,k]}} - \frac{V_e^{[i,k]}(t) - V_e^{[i,k-1]}(t)}{R_a^{[k,k-1]}} \right) \end{aligned}$$

(A.5)

where i, and k stand for the neuron number and the compartment number ($i = 1,2,\dots ,N, k = 1,2,\dots ,26$), ${V_m^{[i,k]}(t)}/{R_m^{[i,k]}} = 0$ at $k=6$, $I_{\mathrm{ion}}^{[i,k]}(t)=0$ at $k\ne 6$, and $I_{\mathrm{syn}}^{[i,k]}(t)$ denotes the synaptic stimuli coming from neurons other than ith neuron to the kth compartment determined randomly from 8th to 26th compartment in ith neuron (see Fig. 1b). To solve with Crank–Nicolson method, (A.5) is rearranged as follows:

$$\begin{aligned}&C_m^{[k]}\frac{V_m^{[i,k]}(t+\varDelta t) - V_m^{[i,k]}(t)}{\varDelta t}\nonumber \\&\quad =\frac{1}{2}\bigg \{ \frac{V_m^{[i,k+1]}(t)-V_m^{[i,k]}(t)}{R_a^{[k+1,k]}} -\frac{V_m^{[i,k]}(t)-V_m^{[i,k-1]}(t)}{R_a^{[k,k-1]}}\nonumber \\&\qquad +\frac{V_m^{[i,k]}(t)}{R_m^{[k]}} +\frac{V_m^{[i,k+1]}(t+\varDelta t)-V_m^{[i,k]}(t+\varDelta t)}{R_a^{[k+1,k]}}\nonumber \\&\qquad -\frac{V_m^{[i,k]}(t+\varDelta t)-V_m^{[i,k-1]}(t+\varDelta t)}{R_a^{[k,k-1]}} +\frac{V_m^{[i,k]}(t+\varDelta t)}{R_m^{[k]}} \bigg \}\nonumber \\&\qquad +\frac{V_e^{[i,k+1]}(t)-V_e^{[i,k]}(t)}{R_a^{[k+1,k]}} -\frac{V_e^{[i,k]}(t)-V_e^{[i,k-1]}(t)}{R_a^{[k,k-1]}}\nonumber \\&\qquad - I_{\mathrm{ion}}^{[i,k]}(t) { - I_{\mathrm{syn}}^{[i,k]}(t) }. \end{aligned}$$

(A.6)

1.2 Ion channel’s equation in soma

We assumed parallel equivalent circuit with seven conductances in the soma (Warman et al. 1994; Stacey and Durand 2000). Briefly, transmembrane current $I^{[i,6]}_{\mathrm{ion}}(t)$ is described by

$$\begin{aligned} I^{[i,6]}_{\mathrm{ion}}(t)= & {} I^{[i]}_{\mathrm{Na}}(t) + I^{[i]}_{K_{\mathrm{DR}}}(t) + I^{[i]}_{K_{M}}(t) + I^{[i]}_{K_{A}}(t)\nonumber \\&+ I^{[i]}_{\mathrm{Ca}}(t) + I^{[i]}_{K_{\mathrm{CT}}}(t) + I^{[i]}_{K_{\mathrm{AHP}}}(t). \end{aligned}$$

(A.7)

One sodium, three active potassium, one calcium, and two calcium-dependent potassium channel currents are incorporated into soma. These current can be expressed as follows:

$$\begin{aligned} I^{[i]}_{\mathrm{Na}}(t)= & {} g_{\mathrm{Na}} m_{[i]}^3(t) h_{[i]}(t) (V_m^{[i,6]}(t)-E_{\mathrm{Na}})\nonumber \\ I^{[i]}_{K_{\mathrm{DR}}}(t)= & {} g_{K_{\mathrm{DR}}} n_{[i]}^4(t) (V_m^{[i,6]}(t)-E_{K_{\mathrm{DR}}})\nonumber \\ I^{[i]}_{K_M}(t)= & {} g_{K_M} u_{[i]}^2(t) (V_m^{[i,6]}(t)-E_{K_M})\nonumber \\ I^{[i]}_{K_A}(t)= & {} g_{K_A} a_{[i]}(t) b_{[i]}(t) (V_m^{[i,6]}(t)-E_{K_A})\nonumber \\ I^{[i]}_{\mathrm{Ca}}(t)= & {} g_{\mathrm{Ca}} s_{[i]}^2(t) r_{[i]}(t) (V_m^{[i,6]}(t)-E_{\mathrm{Ca}})\nonumber \\ I^{[i]}_{K_{\mathrm{AHP}}}(t)= & {} g_{K_{\mathrm{AHP}}} q_{[i]}(t) (V_m^{[i,6]}(t)-E_{K_{\mathrm{AHP}}})\nonumber \\ I^{[i]}_{K_{\mathrm{CT}}}(t)= & {} g_{K_{\mathrm{CT}}} c_{[i]}^2(t) d_{[i]}(t) (V_m^{[i,6]}(t)-E_{K_{\mathrm{CT}}}) \end{aligned}$$

(A.8)

where $m_{[i]}(t)$, $h_{[i]}(t)$ ,$n_{[i]}(t)$, $u_{[i]}(t)$, $a_{[i]}(t)$, $b_{[i]}(t)$, $r_{[i]}(t)$, $q_{[i]}(t)$, $c_{[i]}(t)$ and $d_{[i]}(t)$ are channel opening rates obtained by differential equations of each ion channel. These are determined by $V_m^{[i,6]}(t)$, $E_{\mathrm{rest}}$, $g_x$ and $E_x$, the membrane potential of soma, the resting potential of soma, conductance and reversal potential, respectively.