Abstract
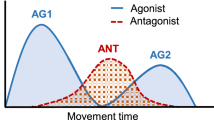
In human upper-arm reaching movements, the variance of the hand position increases until the middle of the movement and then decreases toward the endpoint. Such decrease in positional variance has been suggested as an evidence to support the hypothesis that our nervous system uses feedback control, rather than feedforward control, for arm reaching tasks. In this study, we computed the optimal trajectories based on feedforward control under several criteria for a one-link two-muscle arm model with considering the stochastic property of muscle activities in order to reexamine the hypothesis. The results showed that the feedforward control also represents the decrease in positional variance in the latter half of the movement when the control signal is planned under the minimum energy cost and minimum variance models. Furthermore, the optimal trajectory that minimizes energy cost represents not only the decrease in positional variance but also many other characteristics of the human reaching movements, e.g., the three-phasic activity of antagonistic muscle, bell-shaped speed curve, N-shaped equilibrium trajectory, and bimodal profile of joint stiffness. These results suggest that minimum energy cost model well expresses the characteristics of hand reaching movements, and our central nervous system would make use of not only a feedback control but also feedforward control.







Similar content being viewed by others
References
Adam A, Luca CJD, Erim Z (1998) Hand dominance and motor unit firing behavior. J Neurophysiol 80(3):1373–1382. https://doi.org/10.1152/jn.1998.80.3.1373
Alexander RM (1997) A minimum energy cost hypothesis for human arm trajectories. Biol Cybern 76(2):97–105. https://doi.org/10.1007/s004220050324
Bennett DJ (1993) Torques generated at the human elbow joint in response to constant position errors imposed during voluntary movements. Exp Brain Res 95:488–498. https://doi.org/10.1007/BF00227142
Christou EA, Grossman M, Carlton LG (2002) Modeling variability of force during isometric contractions of the quadriceps femoris. J Mot Behav 34(1):67–81. https://doi.org/10.1080/00222890209601932
Cluff T, Scott SH (2015) Apparent and actual trajectory control depend on the behavioral context in upper limb motor tasks. J Neurosci 35(36):12465–12476. https://doi.org/10.1523/JNEUROSCI.0902-15.2015
Donelan JM, Kram R, Kuo AD (2001) Mechanical and metabolic determinants of the preferred step width in human walking. Proc Biol Sci /R Soc 268(1480):1985–1992. https://doi.org/10.1098/rspb.2001.1761
Dornay M, Uno Y, Kawato M et al (1996) Minimum muscle-tension change trajectories predicted by using a 17-muscle model of the monkey’s arm. J Mot Behav 28(2):83–100. https://doi.org/10.1080/00222895.1996.9941736
Ebner TJ, Pasalar S (2008) Cerebellum predicts the future motor state. Cerebellum 7:583–588. https://doi.org/10.1007/s12311-008-0059-3
Flash T, Hogan N (1985) The coordination of arm movements: an experimentally confirmed mathematical model. J Neurosci 5(7):1688–1703. https://doi.org/10.1523/JNEUROSCI.05-07-01688.1985
Franklin DW, Osu R, Burdet E et al (2003) Adaptation to stable and unstable dynamics achieved by combined impedance control and inverse dynamics model. J Neurophysiol 90(5):3270–3282. https://doi.org/10.1152/jn.01112.2002
Gill PE, Murray W, Saunders MA (2005) Snopt: an SQP algorithm for large-scale constrained optimization. SIAM Rev 47(1):99–131. https://doi.org/10.1137/S0036144504446096
Gribble PL, Mullin LI, Cothros N et al (2003) Role of cocontraction in arm movement accuracy. J Neurophysiol 89(5):2396–2405. https://doi.org/10.1152/jn.01020.2002
Harris CM, Wolpert DM (1998) Signal-dependent noise determines motor planning. Nature 394:780–784. https://doi.org/10.1038/29528
Hogan N (1984) Adaptive control of mechanical impedance by coactivation of antagonist muscles. IEEE Trans Autom Control 29(8):681–690. https://doi.org/10.1109/TAC.1984.1103644
Huang HJ, Kram R, Ahmed AA (2012) Reduction of metabolic cost during motor learning of arm reaching dynamics. J Neurosc 32(6):2182–2190. https://doi.org/10.1523/JNEUROSCI.4003-11.2012
Ito M (2008) Control of mental activities by internal models in the cerebellum. Nat Rev Neurosci 9:304–313. https://doi.org/10.1038/nrn2332
Jones KE, Hamilton AF, Wolpert DM (2002) Sources of signal-dependent noise during isometric force production. J Neurophysiol 88(3):1533–1544. https://doi.org/10.1152/jn.2002.88.3.1533
Julier SJ, Uhlmann JK (1997) New extension of the Kalman filter to nonlinear systems. SPIE 3068:182–193. https://doi.org/10.1117/12.280797
Katayama M, Kawato M (1993) Virtual trajectory and stiffness ellipse during multijoint arm movement predicted by neural inverse models. Biol Cybern 69:353–362. https://doi.org/10.1007/BF01185407
Kawato M (1999) Internal models for motor control and trajectory planning. Curr Opin Neurobiol 9(6):718–727. https://doi.org/10.1016/S0959-4388(99)00028-8
Koike Y, Kawato M (1995) Estimation of dynamic joint torques and trajectory formation from surface electromyography signals using a neural network model. Biol Cybern 73:291–300. https://doi.org/10.1007/BF00199465
Laidlaw DH, Bilodeau M, Enoka RM (2000) Steadiness is reduced and motor unit discharge is more variable in old adults. Muscle Nerve 23(4):600–612
Latash ML, Gottlieb GL (1991) Reconstruction of shifting elbow joint compliant characteristics during fast and slow movements. Neurosci 43(2–3):697–712. https://doi.org/10.1016/0306-4522(91)90328-L
Liu D, Todorov E (2007) Evidence for the flexible sensorimotor strategies predicted by optimal feedback control. J Neurosci 27(35):9354–9368. https://doi.org/10.1523/JNEUROSCI.1110-06.2007
Ma S, Zahalak GI (1991) A distribution-moment model of energetics in skeletal muscle. J Biomech 24(1):21–35. https://doi.org/10.1016/0021-9290(91)90323-F
Miall RC, Wolpert DM (1996) Forward models for physiological motor control. Neural Netw 9(8):1265–1279. https://doi.org/10.1016/S0893-6080(96)00035-4
Minetti AE, Alexander RM (1997) A theory of metabolic costs for bipedal gaits. J Theor Biol 186(4):467–476. https://doi.org/10.1006/jtbi.1997.0407
Morasso P (1981) Spatial control of arm movements. Exp Brain Res 42:223–227. https://doi.org/10.1007/BF00236911
Nagamori A, Laine CM, Loeb GE et al (2021) Force variability is mostly not motor noise: theoretical implications for motor control. PLOS Comput Biol 17(3):e1008707. https://doi.org/10.1371/journal.pcbi.1008707
Nishii J (2000) Legged insects select the optimal locomotor pattern based on the energetic cost. Biol Cybern 83:435–442. https://doi.org/10.1007/s004220000175
Nishii J (2006) An analytical estimation of the energy cost for legged locomotion. J Theor Biol 238(3):636–645. https://doi.org/10.1016/j.jtbi.2005.06.027
Nishii J, Murakami T (2002) Energetic optimality of arm trajectory. In: Proceedings international conference on biomechanics of man, Charles University, Prague, 2002
Nishii J, Taniai Y (2009) Evaluation of trajectory planning models for arm-reaching movements based on energy cost. Neural comput 21(9):2634–2647. https://doi.org/10.1162/neco.2009.06-08-798
Nishii J, Hashizume Y, Kaichida S et al (2012) Constraint and exploitation of redundant degrees of freedom during walking. Robot Auton Syst 60(5):679–684. https://doi.org/10.1016/j.robot.2011.12.006
Osu R, Kamimura N, Iwasaki H et al (2004) Optimal impedance control for task achievement in the presence of signal-dependent noise. J Neurophysiol 92(2):1199–1215. https://doi.org/10.1152/jn.00519.2003
Paulignan Y, MacKenzie C, Marteniuk R et al (1991) Selective perturbation of visual input during prehension movements. Exp Brain Res 83:502–512. https://doi.org/10.1007/BF00229827
Schmidt RA, Zelaznik H, Hawkins B et al (1979) Motor-output variability: a theory for the accuracy of rapid motor acts. Psychol Rev 86(5):415–451. https://doi.org/10.1037/0033-295X.86.5.415
Selen LPJ, Beek PJ, van Dieën JH (2005) Can co-activation reduce kinematic variability? a simulation study. Biol Cybern 93:373–381. https://doi.org/10.1007/s00422-005-0015-y
Selen LPJ, Beek PJ, van Dieën JH (2006) Impedance is modulated to meet accuracy demands during goal-directed arm movements. Exp Brain Res 172:129–138. https://doi.org/10.1007/s00221-005-0320-7
Sherwood DE, Schmidt RA, Walter CB (1988) The force/force-variability relationship under controlled temporal conditions. J Mot Behav 20(2):106–116. https://doi.org/10.1080/00222895.1988.10735436
Taniai Y, Nishii J (2015) Optimality of upper-arm reaching trajectories based on the expected value of the metabolic energy cost. Neural Comput 27(8):1721–1737. https://doi.org/10.1162/NECO_a_00757
Taylor AM, Christou EA, Enoka RM (2003) Multiple features of motor-unit activity influence force fluctuations during isometric contractions. J Neurophysiol 90(2):1350–1361. https://doi.org/10.1152/jn.00056.2003
Todorov E, Jordan M (2002) Optimal feedback control as a theory of motor coordination. Nat neurosci 5:1226–1235. https://doi.org/10.1038/nn963
Todorov E, Li W (2005) A generalized iterative LQG method for locally-optimal feedback control of constrained nonlinear stochastic systems. Proceedings of the 2005, American Control Conference 1:300–306. https://doi.org/10.1109/ACC.2005.1469949
Yeom HG, Kim JS, Chung CK (2020) Brain mechanisms in motor control during reaching movements: transition of functional connectivity according to movement states. Sci Rep 10:567. https://doi.org/10.1038/s41598-020-57489-7
Zarrugh MY, Radcliffe CW (1978) Predicting metabolic cost of level walking. Eur J Appl Physiol Occup Physiol 38:215–223. https://doi.org/10.1007/BF00430080
Zhang L, Straube A, Eggert T (2016) Under threshold position control, peripheral mechanisms compensate efficiently for small perturbations of arm movements. Mot Control 20(1):87–108. https://doi.org/10.1123/mc.2014-0084
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
The authors have no competing interests to declare that are relevant to the content of this article.
Additional information
Communicated by Benjamin Lindner.
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
About this article
Cite this article
Taniai, Y., Naniwa, T. & Nishii, J. Optimal reaching trajectories based on feedforward control. Biol Cybern 116, 517–526 (2022). https://doi.org/10.1007/s00422-022-00939-4
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00422-022-00939-4