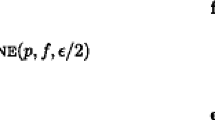Skip to main content
SpringerLink
Log in

Routing Flow Through a Strongly Connected Graph

  • Published:
Algorithmica Aims and scope Submit manuscript

Abstract

It is shown that, for every strongly connected network in which every edge has capacity at least Δ , linear time suffices to send flow from source vertices, each with a given supply, to sink vertices, each with a given demand, provided that the total supply equals the total demand and is bounded by Δ . This problem arises in a maximum-flow algorithm of Goldberg and Rao, the binary blocking flow algorithm.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

Author information

Authors and Affiliations

  1. Computer Engineering and Networks Laboratory, Eidgenössische Technische Hochschule Zürich, CH-8092 Zürich, Switzerland. erlebach@tik.ee.ethz.ch., CH

    Erlebach

  2. Institut für Informatik, Johann Wolfgang Goethe-Universität Frankfurt, D-60054 Frankfurt am Main, Germany. hagerup@ka.informatik.uni-frankfurt.de., DE

    Hagerup

Authors
  1. Erlebach
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Hagerup
    View author publications

    You can also search for this author in PubMed Google Scholar

Rights and permissions

Reprints and permissions

About this article

Cite this article

Erlebach, Hagerup Routing Flow Through a Strongly Connected Graph . Algorithmica 32, 467–473 (2002). https://doi.org/10.1007/s00453-001-0082-y

Download citation

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00453-001-0082-y

Search

Navigation