Skip to main content

Advertisement

Springer Nature Link
Log in

A Universal Online Caching Algorithm Based on Pattern Matching

  • Published:
Algorithmica Aims and scope Submit manuscript

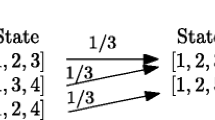
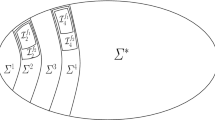
Abstract

We present a universal algorithm for the classical online problem of caching or demand paging. We consider the caching problem when the page request sequence is drawn from an unknown probability distribution and the goal is to devise an efficient algorithm whose performance is close to the optimal online algorithm which has full knowledge of the underlying distribution. Most previous works have devised such algorithms for specific classes of distributions with the assumption that the algorithm has full knowledge of the source. In this paper, we present a universal and simple algorithm based on pattern matching for mixing sources (includes Markov sources). The expected performance of our algorithm is within 4+o(1) times the optimal online algorithm (which has full knowledge of the input model and can use unbounded resources).

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. Aho, A., Denning, P., Ullman, J.D.: Principles of optimal page replacement. J. Assoc. Comput. Mach. 18(1), 80–93 (1971)

    MATH  MathSciNet  Google Scholar 

  2. Algoet, P.: Universal schemes for prediction, gambling and portfolio selection. Ann. Probab. 20(2), 901–941 (1992)

    Article  MATH  MathSciNet  Google Scholar 

  3. Cover, T.M., Thomas, J.A.: Elements of Information Theory. Wiley, New York (1991)

    Book  MATH  Google Scholar 

  4. Curewitz, K., Krishnan, P., Vitter, J.S.: Practical prefetching via data compression. In: Proceedings of the ACM SIGMOD International Conference on Management of Data, pp. 257–266 (1993)

  5. El Yaniv, R., Borodin, A.: Online Computation and Competitive Analysis. Cambridge University Press, Cambridge (1998)

    MATH  Google Scholar 

  6. Feder, M., Merhav, N., Gutman, M.: Universal prediction of individual sequences. IEEE Trans. Inf. Theory 38, 1258–1270 (1992)

    Article  MATH  MathSciNet  Google Scholar 

  7. Fiat, A., Karp, R.M., Luby, M., McGeoch, L.A., Sleator, D.D., Young, N.E.: On competitive algorithms for paging problems. J. Algorithms 12, 685–699 (1991)

    Article  MATH  Google Scholar 

  8. Franaszek, P.A., Wagner, T.J.: Some distribution-free aspects of paging performance. J. Assoc. Comput. Mach. 21, 31–39 (1974)

    MATH  MathSciNet  Google Scholar 

  9. Gusfield, D.: Algorithms on Strings, Trees, and Sequences. Cambridge University Press, Cambridge (1997)

    MATH  Google Scholar 

  10. Hannan, J.F.: Approximation to Bayes risk in repeated plays. In: Contributions to the Theory of Games. Annals of Mathematics Studies, vol. 3, pp. 97–139. Princeton Univ. Press, Princeton (1957)

    Google Scholar 

  11. Jacquet, P., Szpankowski, W., Apostol, I.: A universal predictor based on pattern matching. IEEE Trans. Inf. Theory 48(6), 1462–1472 (2002)

    Article  MATH  MathSciNet  Google Scholar 

  12. Karlin, A.R., Phillips, S.J., Raghavan, P.: Markov paging. SIAM J. Comput. 30(3), 906–922 (2000)

    Article  MATH  MathSciNet  Google Scholar 

  13. Lund, C., Phillips, S., Reingold, N.: Paging against a distribution and IP networking. J. Comput. Syst. Sci. 58, 222–231 (1999)

    Article  MATH  MathSciNet  Google Scholar 

  14. Merhav, N., Feder, M.: Universal prediction. IEEE Trans. Inf. Theory 44, 2124–2147 (1998)

    Article  MATH  MathSciNet  Google Scholar 

  15. Merhav, N., Ordentlich, E., Seroussi, G., Weinberger, M.J.: On sequential strategies for loss functions with memory. IEEE Trans. Inf. Theory 48(7), 1947–1958 (2002)

    Article  MATH  MathSciNet  Google Scholar 

  16. Mitzenmacher, M., Upfal, E.: Probability and Computing: Randomized Algorithms and Probabilistic Analysis. Cambridge University Press, Cambridge (2005)

    MATH  Google Scholar 

  17. Motwani, R., Raghavan, P.: Randomized Algorithms. Cambridge University Press, Cambridge (1995)

    MATH  Google Scholar 

  18. Pandurangan, G., Upfal, E.: Entropy-based bounds for online algorithms. ACM Trans. Algorithms 3(1) (2007)

  19. Sleator, D.D., Tarjan, R.E.: Amortized efficiency of list update and paging rules. Commun. ACM 28(2), 202–208 (1985)

    Article  MathSciNet  Google Scholar 

  20. Szpankowski, W.: Average Case Analysis of Algorithms on Sequences. Wiley, New York (2001)

    MATH  Google Scholar 

  21. Vitter, J.S., Krishnan, P.: Optimal prefetching via data compression. J. Assoc. Comput. Mach. 43(5), 771–793 (1996)

    MATH  MathSciNet  Google Scholar 

  22. Weinberger, M., Ordentlich, E.: On-line decision making for a class of loss functions via Lempel-Ziv parsing. In: Proc. of the IEEE Data Compression Conference, pp. 163–172 (2000)

  23. Ziv, J., Lempel, A.: A universal algorithms for sequential data compression. IEEE Trans. Inf. Theory 23(3), 337–343 (1977)

    Article  MATH  MathSciNet  Google Scholar 

  24. Ziv, J., Lempel, A.: Compression of individual sequences via variable rate coding. IEEE Trans. Inf. Theory 24(5), 530–536 (1978)

    Article  MATH  MathSciNet  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Department of Computer Science, Purdue University, W. Lafayette, IN, 47907, USA

    Gopal Pandurangan & Wojciech Szpankowski

Authors
  1. Gopal Pandurangan
    View author publications

    You can also search for this author inPubMed Google Scholar

  2. Wojciech Szpankowski
    View author publications

    You can also search for this author inPubMed Google Scholar

Corresponding author

Correspondence to Gopal Pandurangan.

Additional information

A preliminary version of this paper was presented at the IEEE International Symposium on Information Theory, Adelaide, Australia, 2005.

The work of Wojciech Szpankowski was supported in part by the NSF Grants CCF-0513636, and DMS-0503742, the NIH Grant R01 GM068959-01, AFOSR Grant 073071, and NSA Grant 07G-044.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Pandurangan, G., Szpankowski, W. A Universal Online Caching Algorithm Based on Pattern Matching. Algorithmica 57, 62–73 (2010). https://doi.org/10.1007/s00453-008-9196-9

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00453-008-9196-9

Keywords