Skip to main content
SpringerLink
Log in

Approximation Algorithms for Minimizing Edge Crossings in Radial Drawings

  • Published:
Algorithmica Aims and scope Submit manuscript

Abstract

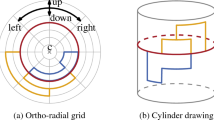
We study a crossing minimization problem of drawing a bipartite graph with a radial drawing of two orbits. Radial drawings are one of well-known drawing conventions in social network analysis and visualization, in particular, displaying centrality indices of actors (Wasserman and Faust, Social Network Analysis: Methods and Applications. Cambridge University Press, Cambridge, 1994). The main problem in this paper is called the one-sided radial crossing minimization, if the positions of vertices in the outer orbit are fixed. The problem is known to be NP-hard (Bachmaier, IEEE Trans. Vis. Comput. Graph. 13, 583–594, 2007), and a number of heuristics are available (Bachmaier, IEEE Trans. Vis. Comput. Graph. 13, 583–594, 2007). However, there is no approximation algorithm for the crossing minimization problem in radial drawings. We present the first polynomial time constant-factor approximation algorithm for the one-sided radial crossing minimization problem.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. Bachmaier, C.: A radial adaptation of the Sugiyama framework for visualizing hierarchical information. IEEE Trans. Vis. Comput. Graph. 13, 583–594 (2007)

    Article  Google Scholar 

  2. Buchner, H.: Displaying centralities using orbital layout. Diploma Thesis, University of Passau, Germany (2006)

  3. Di Battista, G., Eades, P., Tamassia, R., Tollis, I.G.: Graph Drawing: Algorithms for the Visualization of Graphs. Prentice-Hall, Englewood Cliffs (1999)

    MATH  Google Scholar 

  4. Dujmović, V., Whitesides, S.: An efficient fixed parameter tractable algorithm for 1-sided crossing minimization. Algorithmica 40, 15–31 (2004)

    Article  MATH  MathSciNet  Google Scholar 

  5. Dujmović, V., Fernau, H., Kaufmann, M.: Fixed parameter algorithms for one-sided crossing minimization revisited. In: Proc. of Graph Drawing 2003. Lecture Notes in Computer Science, vol. 2912, pp. 332–344. Springer, New York (2004)

    Google Scholar 

  6. Eades, P., Whitesides, S.: Drawing graphs in two layers. Theor. Comput. Sci. 131(2), 361–374 (1994)

    Article  MATH  MathSciNet  Google Scholar 

  7. Eades, P., Wormald, N.C.: Edge crossing in drawing bipartite graphs. Algorithmica 11, 379–403 (1994)

    Article  MATH  MathSciNet  Google Scholar 

  8. Garey, M.R., Johnson, D.S.: Crossing number is NP-complete. SIAM J. Algebr. Discrete Methods 4(3), 312–316 (1983)

    Article  MATH  MathSciNet  Google Scholar 

  9. Di Giacomo, E., Grilli, L., Liotta, G.: Drawing bipartite graphs on two parallel convex curves. J. Graph Algorithms Appl. 12(1), 97–112 (2008)

    MATH  MathSciNet  Google Scholar 

  10. Jünger, M., Mutzel, P.: 2-layer straight line crossing minimization: performance of exact and heuristic algorithms. J. Graph Algorithms Appl. 1, 1–25 (1997)

    MathSciNet  Google Scholar 

  11. Kaufmann, M., Wagner, D. (ed.): Drawing Graphs: Methods and Models. Lecture Notes in Computer Science, vol. 2025. Springer, New York (2001)

    MATH  Google Scholar 

  12. Mutzel, P., Weiskircher, R.: Two-layer planarization in graph drawing. In: Proc. of ISAAC 1998. Lecture Notes in Computer Science, vol. 1533, pp. 69–79. Springer, New York (1998)

    Google Scholar 

  13. Nagamochi, H.: An improved bound on the one-sided minimum crossing number in two-layered drawings. Discrete Comput. Geom. 33, 569–591 (2005)

    Article  MATH  MathSciNet  Google Scholar 

  14. Nagamochi, H., Yamada, N.: Counting edge crossings in a 2-layered drawing. Inf. Process. Lett. 91, 221–225 (2004)

    Article  MATH  MathSciNet  Google Scholar 

  15. Nishizeki, T., Rahman, M.S.: Planar Graph Drawing. World Scientific, Singapore (2004)

    MATH  Google Scholar 

  16. Purchase, H.C.: Which aesthetic has the greatest effect on human understanding? In: Proc. of the 5th International Symposium on Graph Drawing (GD’97). Lecture Notes in Computer Science, vol. 1353, pp. 248–261. Springer, New York (2007)

    Google Scholar 

  17. Shahrokhi, F., Sykora, O., Székly, L.A., Vrto, I.: On bipartite drawings and the linear arrangement problem. SIAM J. Comput. 30, 1773–1789 (2001)

    Article  MATH  MathSciNet  Google Scholar 

  18. Sugiyama, K.: Graph Drawing and Applications. World Scientific, Singapore (2002)

    Book  MATH  Google Scholar 

  19. Sugiyama, K., Tagawa, S., Toda, M.: Methods for visual understanding of hierarchical system structures. IEEE Trans. Syst. Man Cybern. 11, 109–125 (1981)

    Article  MathSciNet  Google Scholar 

  20. Wasserman, S., Faust, K.: Social Network Analysis: Methods and Applications. Cambridge University Press, Cambridge (1994)

    Google Scholar 

  21. Zheng, L., Buchheim, C.: A new exact algorithm for the two-sided crossing minimization problem. In: Proc. of COCOA 2007. Lecture Notes in Computer Science, vol. 4616, pp. 301–310. Springer, New York (2007)

    Google Scholar 

Download references

Author information

Authors and Affiliations

  1. School of Information Technologies, University of Sydney, Sydney, Australia

    Seok-Hee Hong

  2. Department of Applied Mathematics and Physics, Kyoto University, Kyoto, Japan

    Hiroshi Nagamochi

Authors
  1. Seok-Hee Hong
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Hiroshi Nagamochi
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Hiroshi Nagamochi.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Hong, SH., Nagamochi, H. Approximation Algorithms for Minimizing Edge Crossings in Radial Drawings. Algorithmica 58, 478–497 (2010). https://doi.org/10.1007/s00453-009-9277-4

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00453-009-9277-4

Keywords

Search

Navigation