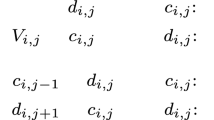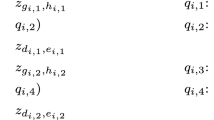Abstract
Let I be a stable matching instance with N stable matchings. For each man m, order his (not necessarily distinct) N partners from his most preferred to his least preferred. Denote the ith woman in his sorted list as p i (m). Let α i consist of the man-woman pairs where each man m is matched to p i (m). Teo and Sethuraman proved this surprising result: for i=1 to N, not only is α i a matching, it is also stable. The α i ’s are called the generalized median stable matchings of I. Determining if these stable matchings can be computed efficiently is an open problem.
In this paper, we present a new characterization of the generalized median stable matchings that provides interesting insights. It implies that the generalized median stable matchings in the middle—α (N+1)/2 when N is odd, α N/2 and α N/2+1 when N is even—are fair not only in a local sense but also in a global sense because they are also medians of the lattice of stable matchings. We then show that there are some families of SM instances for which computing an α i is easy but that the task is NP-hard in general. Finally, we also consider what it means to approximate a median stable matching and present results for this problem.
Similar content being viewed by others
References
Abdulkadiroglu, A., Pathak, P., Roth, A.: The New York City high school match. Am. Econ. Rev., Pap. Proc. 95, 364–367 (2005)
Abdulkadiroglu, A., Pathak, P., Roth, A., Sönmez, T.: The Boston public school match. Am. Econ. Rev., Pap. Proc. 95, 368–371 (2005)
Bandelt, H., Barthelemy, J.: Medians in median graphs. Discrete Appl. Math. 8, 131–142 (1984)
Bansal, V., Agrawal, A., Malhotra, V.: Polynomial time algorithm for an optimal stable assignment with multiple partners. Theor. Comput. Sci. 379, 317–328 (2007)
Barbut, M.: Médiane, distributivité, éloignements, 1961. Math. Sci. Hum. 70, 5–31 (1980) (reprinted)
Birkhoff, G., Kiss, S.: A ternary operation in distributive lattices. Bull. Am. Math. Soc. 53, 749–752 (1947)
Blair, C.: Every finite distributive lattice is a set of stable matchings. J. Comb. Theory A 37, 353–356 (1984)
Cheng, C.: The generalized median stable matchings: finding them is not that easy. In: Proceedings of the 8th Latin Theoretical Informatics Conference, pp. 568–579 (2008)
Cheng, C., McDermid, E., Suzuki, I.: A unified approach to finding good stable matchings in the hospitals/residents setting. Theor. Comput. Sci. 400, 84–99 (2008)
Faigle, U., Lovász, L., Schrader, R., Turán, G.: Searching in trees, series-parallel and interval orders. SIAM J. Comput. 15, 1075–1084 (1986)
Feder, T.: Stable Networks and Product Graphs. Memoirs of the American Mathematical Society, vol. 116. AMS, Providence (1995)
Fleiner, T.: A fixed-point approach to stable matchings and some applications. Math. Oper. Res. 28, 103–126 (2003)
Gale, D., Shapley, L.: College admissions and the stability of marriage. Am. Math. Mon. 69, 9–15 (1962)
Gusfield, D.: Three fast algorithms for four problems in stable marriage. SIAM J. Comput. 16, 111–128 (1987)
Gusfield, D., Irving, R.: The Stable Marriage Problem: Structure and Algorithms. The MIT Press, Cambridge (1989)
Irving, R., Leather, P.: The complexity of counting stable marriages. SIAM J. Comput. 15, 655–667 (1986)
Kijima, S., Nemoto, T.: Randomized approximation for the generalize median stable matchings. A preprint, RIMS-1648 (2008)
Klaus, B., Klijn, F.: Median stable matchings for college admissions. Int. J. Game Theory 34, 1–11 (2006)
LeClerc, B.: Medians and majorities in semimodular lattices. SIAM J. Discrete Math. 3, 266–276 (1990)
Möhring, R.: Computationally tractable classes of ordered sets. In: Rival, I. (ed.) Algorithms and Order, pp. 105–193. Kluwer Academic, Dordrecht (1989)
Monjardet, B.: Théorie et application de la médiane dans les treillis distributifs finis. Ann. Discrete Math. 9, 87–91 (1980)
Nemoto, T.: Some remarks on the median stable marriage problem. In: Proceedings of the 17th International Symposium on Mathematical Programming (2000)
Provan, J., Ball, M.: The complexity of counting cuts and of computing the probability that a graph is connected. SIAM J. Comput. 12, 777–788 (1983)
Roth, A., Peranson, E.: The redesign of the matching market of American physicians: Some engineering aspects of economic design. Am. Econ. Rev. 89, 748–780 (1999)
Steiner, G.: Single machine scheduling with precedence constraints of dimension 2. Math. Oper. Res. 9, 248–259 (1984)
Steiner, G.: Searching in 2-dimensional partial orders. J. Algorithms 8, 95–105 (1987)
Teo, C.-P., Sethuraman, J.: The geometry of fractional stable matchings and its applications. Math. Oper. Res. 23, 874–891 (1998)
Author information
Authors and Affiliations
Corresponding author
Additional information
A preliminary version [8] of this paper was presented at LATIN 2008.
The research of C.T. Cheng was supported by NSF Award No. CCF-0830678.
Rights and permissions
About this article
Cite this article
Cheng, C.T. Understanding the Generalized Median Stable Matchings. Algorithmica 58, 34–51 (2010). https://doi.org/10.1007/s00453-009-9307-2
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00453-009-9307-2