Skip to main content
SpringerLink
Log in

Tile Complexity of Approximate Squares

  • Published:
Algorithmica Aims and scope Submit manuscript

Abstract

The standard Tile Assembly Model (TAM) of Winfree (Algorithmic self-assembly of DNA, Ph.D. thesis, 1998) is a mathematical theory of crystal aggregations via monomer additions with applications to the emerging science of DNA self-assembly. Self-assembly under the rules of this model is programmable and can perform Turing universal computation. Many variations of this model have been proposed and the canonical problem of assembling squares has been studied extensively.

We consider the problem of building approximate squares in TAM. Given any \(\varepsilon \in (0,\frac{1}{4}]\) we show how to construct squares whose sides are within (1±ε)N of any given positive integer N using \(O( \frac{\log \frac{1}{\varepsilon}}{\log \log\frac{1}{\varepsilon}} + \frac{\log \log \varepsilon N}{\log \log \log \varepsilon N} )\) tile types. We prove a matching lower bound by showing that \(\varOmega( \frac{\log \frac{1}{\varepsilon}}{\log \log\frac{1}{\varepsilon}} + \frac{\log \log \varepsilon N}{\log \log \log \varepsilon N} )\) tile types are necessary almost always to build squares of required approximate dimensions. In comparison, the optimal construction for a square of side exactly N in TAM uses \(O(\frac{\log N}{\log \log N})\) tile types.

The question of constructing approximate squares has been recently studied in a modified tile assembly model involving concentration programming. All our results are trivially translated into the concentration programming model by assuming arbitrary (non-zero) concentrations for our tile types. Indeed, the non-zero concentrations could be chosen by an adversary and our results would still hold.

Our construction can get highly accurate squares using very few tile types and are feasible starting from values of N that are orders of magnitude smaller than the best comparable constructions previously suggested. At an accuracy of ε=0.01, the number of tile types used to achieve a square of size 107 is just 58 and our constructions are proven to work for all N≥13130. If the concentrations of the tile types are carefully chosen, we prove that our construction assembles an L×L square in optimal assembly time O(L) where (1−ε)N≤L≤(1+ε)N.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4

Similar content being viewed by others

Notes

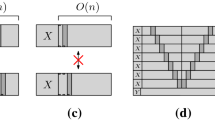
  1. The face labels merely depict the bits of the counter and do not play any role in tile binding. Here, they are identical to the North pad type.

References

  1. Adleman, L., Cheng, Q., Goel, A., Huang, M.D.: Running time and program size for self-assembled squares. In: Symposium on Theory of Computing, pp. 740–748 (2001)

    Google Scholar 

  2. Aggarwal, G., Cheng, Q., Goldwasser, M.H., Kao, M.Y., de Espanes, P.M., Schweller, R.T.: Complexities for generalized models of self-assembly. SIAM J. Comput. 34(6), 1493–1515 (2005)

    Article  MathSciNet  MATH  Google Scholar 

  3. Andersen, E., Dong, M., Nielsen, M., Jahn, K., Subramani, R., Mamdouh, W., Golas, M., Sander, B., Stark, H., Oliveira, C., Pedersen, J.S., Birkedal, V., Besenbacher, F., Gothelf, K., Kjems, J.: Self-assembly of a nanoscale DNA box with a controllable lid. Nature 459(7243), 73–76 (2009)

    Article  Google Scholar 

  4. Barish, R., Rothemund, P., Winfree, E.: Two computational primitives for algorithmic self-assembly: copying and counting. Nano Lett. 5, 2586–2592 (2005)

    Article  Google Scholar 

  5. Becker, F., Rapaport, I., Remila, E.: Self-assemblying classes of shapes with a minimum number of tiles, and in optimal time. In: Foundations of Software Technology and Theoretical Computer Science, pp. 45–56 (2006)

    Google Scholar 

  6. Becker, F., Remila, E., Schabanel, N.: Time optimal self-assembling of 2D and 3D shapes: the case of squares and cubes. In: Goel, A., Simmel, F., Sosík, P. (eds.) DNA Computing. Lecture Notes in Computer Science, vol. 5347, pp. 144–155. Springer, Berlin (2009)

    Chapter  Google Scholar 

  7. Berger, R.: The undecidability of the domino problem. Mem. Am. Math. Soc. 66, 1–72 (1966)

    Google Scholar 

  8. Chandran, H., Gopalkrishnan, N., Reif, J.: The tile complexity of linear assemblies. In: International Colloquium on Automata, Languages and Programming, pp. 235–253 (2009)

    Chapter  Google Scholar 

  9. Chen, H.L., Goel, A.: Error free self-assembly using error prone tiles. In: Ferretti, C., Mauri, G., Zandron, C. (eds.) DNA Computing. Lecture Notes in Computer Science, vol. 3384, pp. 702–707. Springer, Berlin (2005)

    Google Scholar 

  10. Demaine, E., Demaine, M., Fekete, S., Ishaque, M., Rafalin, E., Schweller, R., Souvaine, D.: Staged self-assembly: nanomanufacture of arbitrary shapes with O(1) glues. Nat. Comput. 7(3), 347–370 (2008)

    Article  MathSciNet  MATH  Google Scholar 

  11. Dietz, H., Douglas, S., Shih, W.: Folding DNA into twisted and curved nanoscale shapes. Science 325(5941), 725–730 (2009)

    Article  Google Scholar 

  12. Dirks, R., Pierce, N.: Triggered amplification by hybridization chain reaction. Proc. Natl. Acad. Sci. USA 101(43), 15275–15278 (2004)

    Article  Google Scholar 

  13. Doty, D.: Randomized self-assembly for exact shapes. SIAM J. Comput. 39(8), 3521–3552 (2010)

    Article  MathSciNet  MATH  Google Scholar 

  14. Doty, D., Patitz, M., Summers, S.: Limitations of self-assembly at temperature 1. Theor. Comput. Sci. 412(1–2), 145–158 (2011)

    Article  MathSciNet  MATH  Google Scholar 

  15. Douglas, S., Dietz, H., Liedl, T., Hogberg, B., Graf, F., Shih, W.: Self-assembly of DNA into nanoscale three-dimensional shapes. Nature 459(7245), 414–418 (2009)

    Article  Google Scholar 

  16. Garey, M., Johnson, D.: Computers and Intractability: A Guide to the Theory of NP-Completeness. Freeman, New York (1981)

    Google Scholar 

  17. Kao, M.Y., Schweller, R.: Reducing tile complexity for self-assembly through temperature programming. In: Symposium on Discrete Algorithms, pp. 571–580 (2006)

    Google Scholar 

  18. Kao, M.Y., Schweller, R.: Randomized self-assembly for approximate shapes. In: International Colloquium on Automata, Languages and Programming, pp. 370–384 (2008)

    Chapter  Google Scholar 

  19. LaBean, T., Yan, H., Kopatsch, J., Liu, F., Winfree, E., Reif, J., Seeman, N.: Construction, analysis, ligation, and self-assembly of DNA triple crossover complexes. J. Am. Chem. Soc. 122(9), 1848–1860 (2000)

    Article  Google Scholar 

  20. Lewis, H., Papadimitriou, C.: Elements of the Theory of Computation. Prentice Hall, New York (1981)

    MATH  Google Scholar 

  21. Mao, C., Labean, T., Reif, J., Seeman, N.: Logical computation using algorithmic self-assembly of DNA triple-crossover molecules. Nature 407, 493–496 (2000)

    Article  Google Scholar 

  22. Park, S.H., Yin, P., Liu, Y., Reif, J., LaBean, T., Yan, H.: Programmable DNA self-assemblies for nanoscale organization of ligands and proteins. Nano Lett. 5, 729–733 (2005)

    Article  Google Scholar 

  23. Reif, J., Sahu, S., Yin, P.: Compact error-resilient computational DNA tiling assemblies. In: Ferretti, C., Mauri, G., Zandron, C. (eds.) DNA Computing. Lecture Notes in Computer Science, vol. 3384, pp. 293–307. Springer, Berlin (2005)

    Chapter  Google Scholar 

  24. Robinson, R.: Undecidability and nonperiodicity for tilings of the plane. Invent. Math. 12, 177–209 (1971)

    Article  MathSciNet  Google Scholar 

  25. Rothemund, P.: Folding DNA to create nanoscale shapes and patterns. Nature 440, 297–302 (2006)

    Article  Google Scholar 

  26. Rothemund, P., Papadakis, N., Winfree, E.: Algorithmic self-assembly of DNA Sierpinski triangles. PLoS Biology 2(12), e424 (2004), pp. 2041–2053

    Article  Google Scholar 

  27. Rothemund, P., Winfree, E.: The program-size complexity of self-assembled squares. In: Symposium on Theory of Computing, pp. 459–468 (2000)

    Google Scholar 

  28. Schulman, R., Winfree, E.: Programmable control of nucleation for algorithmic self-assembly. SIAM J. Comput. 39(4), 1581–1616 (2009)

    Article  MathSciNet  MATH  Google Scholar 

  29. Wang, H.: Proving theorems by pattern recognition II. Bell Syst. Tech. J. 40, 1–41 (1961)

    Google Scholar 

  30. Winfree, E.: On the computational power of DNA annealing and ligation. In: DNA Based Computers. DIMACS, vol. 27, pp. 199–221. Am. Math. Soc., Providence (1995)

    Google Scholar 

  31. Winfree, E.: Algorithmic self-assembly of DNA. Ph.D. thesis, California Institute of Technology (1998)

  32. Winfree, E., Bekbolatov, R.: Proofreading tile sets: error correction for algorithmic self-assembly. In: Chen, J., Reif, J. (eds.) DNA Computing, Lecture Notes in Computer Science, vol. 2943, pp. 1980–1981. Springer, Berlin (2004)

    Chapter  Google Scholar 

  33. Winfree, E., Liu, F., Wenzler, L., Seeman, N.: Design and self-assembly of two-dimensional DNA crystals. Nature 394, 539–544 (1998)

    Article  Google Scholar 

  34. Winfree, E., Yang, X., Seeman, N.: Universal computation via self-assembly of DNA: some theory and experiments. In: DNA Based Computers II. DIMACS, vol. 44, pp. 191–213. Am. Math. Soc., Providence (1996)

    Google Scholar 

  35. Yan, H., Feng, L., LaBean, T., Reif, J.: Parallel molecular computation of pair-wise XOR using DNA string tile. J. Am. Chem. Soc. 125(47), 14246–14247 (2003)

    Article  Google Scholar 

  36. Yin, P., Choi, H., Calvert, C., Pierce, N.: Programming biomolecular self-assembly pathways. Nature 451(7176), 318–322 (2008)

    Article  Google Scholar 

  37. Yin, P., Yan, H., Daniell, X., Turberfield, A., Reif, J.: A unidirectional DNA Walker moving autonomously along a linear track. Angew. Chem., Int. Ed. 116(37), 5014–5019 (2004)

    Article  Google Scholar 

  38. Zhang, D., Turberfield, A., Yurke, B., Winfree, E.: Engineering entropy-driven reactions and networks catalyzed by DNA. Science 318, 1121–1125 (2007)

    Article  Google Scholar 

Download references

Acknowledgements

We thank our reviewers for pointing out errors and for comments that improve the readability of the paper. This work was supported by NSF EMT Grants CCF-0829797 and CCF-0829798.

Author information

Authors and Affiliations

  1. Department of Computer Science, Duke University, Durham, NC, 27708, USA

    Harish Chandran, Nikhil Gopalkrishnan & John Reif

  2. Adjunct, Computing and Information Technology, King Abdulaziz University, Jeddah, Saudi Arabia

    John Reif

Authors
  1. Harish Chandran
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Nikhil Gopalkrishnan
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. John Reif
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Nikhil Gopalkrishnan.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Chandran, H., Gopalkrishnan, N. & Reif, J. Tile Complexity of Approximate Squares. Algorithmica 66, 1–17 (2013). https://doi.org/10.1007/s00453-012-9620-z

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00453-012-9620-z

Keywords

Search

Navigation