Speed Scaling on Parallel Processors

Abstract

In this paper we investigate dynamic speed scaling, a technique to reduce energy consumption in variable-speed microprocessors. While prior research has focused mostly on single processor environments, in this paper we investigate multiprocessor settings. We study the basic problem of scheduling a set of jobs, each specified by a release date, a deadline and a processing volume, on variable-speed processors so as to minimize the total energy consumption.

We first settle the problem complexity if unit size jobs have to be scheduled. More specifically, we devise a polynomial time algorithm for jobs with agreeable deadlines and prove NP-hardness results if jobs have arbitrary deadlines. For the latter setting we also develop a polynomial time algorithm achieving a constant factor approximation guarantee. Additionally, we study problem settings where jobs have arbitrary processing requirements and, again, develop constant factor approximation algorithms. We finally transform our offline algorithms into constant competitive online strategies.

Appendix

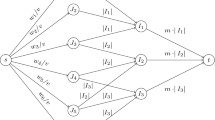
In this appendix we establish the NP-hardness results stated in Theorems 2 and 3 based on the reduction described in Section 3. Given a schedule S, let l _S (i) be the total length of intervals in S where job i is executed. The energy consumption of job i is at least (1/l _S (i))^α−1. Furthermore, for a set $\mathcal{S}$ of jobs (or intervals in S) let $l(\mathcal{S})$ ($l_{S}(\mathcal{S})$, respectively) denote the sum of the lengths of all jobs (intervals) in $\mathcal{S}$.

We will determine the minimum energy necessary to schedule $\mathcal{J}$ on m processors. To this end we need two lemmas on the structure of an optimal schedule for $\mathcal{J}$.

Lemma 9

In any optimal schedule S for $\mathcal{J}$ no two jobs numbered larger than n are executed on the same processor.

Proof

Consider an optimal schedule S and assume for the sake of contradiction there were jobs i>n and i′>n running on the same processor j. Then one of the two jobs, say job i, is executed in intervals of total length at most 3d(n)/2 and incurs an energy consumption of at least (2/(3d(n)))^α−1. Furthermore, there must exist one processor on which no job is executed in the interval [d(n),3d(n)) because we have only m jobs with a deadline greater than d(n) and two of these are executed on processor j. We can now schedule job i in this idle period, generating an energy consumption of at most (1/(2d(n)))^α−1 for job i. This is less than the initial consumption, contradicting the optimality of the considered schedule. □

Lemma 10

In any optimal schedule S for $\mathcal{J}$ each job i, with 1≤i≤n, is processed continuously throughout its execution interval [r(i),d(i)).

Proof

Consider any optimal schedule S. A first observation is that S does not contain processor idle times, i.e. each processor executes jobs throughout [0,3d(n)): Suppose there were some processor j and an interval I⊆[0,3d(n)) during which the processor would not execute any job. By Lemma 9 some job n+k, where 1≤k≤m, is executed in processor j. We now modify S by executing job n+k additionally during I. Thereby we reduce the speed needed to process job n+k and hence the total energy of the schedule.

Assume that in S some job i is not executed over its full possible interval I=[r(i),d(i)), i.e. l _S (i)=l(i)−ε for some 0<ε<l(i). Since the execution intervals of all jobs i′ with 1≤i′≤n are pairwise disjoint, no such job i′≠i can be scheduled in I. Hence, by the above observation, some job n+k, with 1≤k≤m, is partially executed in I on the processor where i is scheduled. As shown in Lemma 9 only this one job is processed in I. Furthermore, l _S (n+k)>2d(n). Now we can construct a better schedule by executing job i over its full possible length l(i) and reducing the execution interval of job n+k by ϵ. This modified schedule has a strictly smaller energy consumption because the energy consumed by jobs i and n+k satisfies

$$\underbrace{ \biggl(\frac{1}{l_S(i)} \biggr)^{\alpha-1}+ \biggl( \frac{1}{l_S(n+k)} \biggr)^{\alpha-1} }_{\textrm{energy consumption in initial schedule}} \\ > \underbrace{ \biggl(\frac{1}{l_S(i)+\varepsilon} \biggr)^{\alpha-1} + \biggl( \frac{1}{l_S(n+k)-\varepsilon} \biggr)^{\alpha-1} }_{\textrm{energy consumption in new schedule}}. $$

This follows from Lemma 1, by setting c=l _S (n+k)+l _S (i) and x=l _S (i). We note that l _S (i)<l _S (i)+ε=l(i)<c/2 as l(i)≤d(n) and l _S (n+k)>2d(n). This contradicts the assumption that schedule S was optimal. □

Theorem 9

Let A⊂ℤ⁺, m∈ℕ and B=(∑ _a∈A a)/m. (A,m)∈Multi- Partition if and only if an optimal schedule for $\mathcal{J}$ incurs an energy of

$$E_{OPT} = \sum_{i=1}^{n} \biggl( \frac{1}{l(i)} \biggr)^{\alpha-1} + m \biggl(\frac{1}{3d(n)-B} \biggr)^{\alpha-1}. $$

Proof

By Lemma 10, in any optimal schedule each job i, with 1≤i≤n, is processed continuously throughout its execution interval [r(i),d(i)). Hence it requires an energy of exactly (1/l(i))^α−1, and the total energy spent for jobs 1,…,n is $\sum_{i=1}^{n}(1/l(i))^{\alpha-1}$. Thus the energy consumption of an optimal solution depends only on the energy consumed by jobs n+1,n+2,…,n+m. Let k∈{1,2,…,m}. By Lemma 9, all these jobs are executed on separate machines. We assume w.l.o.g. that job n+k is executed on processor k. Let $\mathcal{J}_{k}\subseteq\{1, 2,\ldots, n\}$ be the set of jobs scheduled on processor k. We can now easily compute the energy used by n+k as

$$\biggl({1\over l_S(n+k)} \biggr)^{\alpha-1} = \biggl( \frac{1}{3d(n)- \sum_{i\in \mathcal{J}_k}l(i)} \biggr)^{\alpha-1}. $$

By Lemma 1 we find that the sum of the energy consumptions of jobs n+1,n+2,…,n+m is minimal if and only if l _S (n+1)=l _S (n+2)=…=l _S (n+m). This is the case if and only if $\sum_{i\in \mathcal{J}_{1}}l(i) = \sum_{i\in \mathcal{J}_{2}}l(i)=\ldots = \sum_{i\in \mathcal{J}_{m}}l(i) = d(n)/m=B$. By our construction this is possible if and only if there exist sets A ₁,A ₂,…,A _m ⊆A with $\bigcup_{i=1}^{m} A_{i}=A$ and, for all i≠j, there holds A _i ∩A _j =∅ as well as $\sum_{a\in A_{i}}a =\sum_{a\in A_{j}}a$. Finally, this is the case if and only if (A,m)∈Multi-Partition. □

We are now ready to derive the desired NP-hardness results. Setting m=2, the NP-hard Partition problem [18] is a special case of our Multi-Partition problem. Theorem 9 yields Theorem 2. Another special case of Multi-Partition is 3-Partition. In this case A satisfies the property that there exists a B∈ℤ⁺ such that, for all a∈A, we have B/4<a<B/2 and ∑ _a∈A a=mB. Since 3-Partition is strongly NP-hard [18], we obtain Theorem 3 as a consequence of Theorem 9.