Skip to main content

Advertisement

Springer Nature Link
Log in

Linear Recognition and Embedding of Fibonacci Cubes

  • Published:
Algorithmica Aims and scope Submit manuscript

Abstract

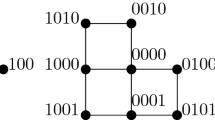
Fibonacci strings are binary strings that contain no two consecutive 1s. The Fibonacci cube Γ h is the subgraph of the h-cube induced by the Fibonacci strings. These graphs are applicable as interconnection networks and in theoretical chemistry, and lead to the Fibonacci dimension of a graph. We derive a new characterization of Fibonacci cubes. The characterization is the basis for an algorithm which recognizes these graphs in linear time. Moreover, a graph which was recognized as a Fibonacci cube can be embedded into a hypercube using Fibonacci strings within the same time bound.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2

Similar content being viewed by others

Explore related subjects

Discover the latest articles and news from researchers in related subjects, suggested using machine learning.

References

  1. Aurenhammer, F., Hagauer, J.: Recognizing binary Hamming graphs in O(n 2logn) time. Math. Syst. Theory 28, 387–395 (1995)

    Article  MATH  MathSciNet  Google Scholar 

  2. Cabello, S., Eppstein, D., Klavžar, S.: The Fibonacci dimension of a graph. Electron. J. Comb. 18, P55 (2011)

    Google Scholar 

  3. Eppstein, D.: Recognizing partial cubes in quadratic time. J. Graph Algorithms Appl. 15, 269–293 (2011)

    Article  MathSciNet  Google Scholar 

  4. Hammack, R., Imrich, W., Klavžar, S.: Handbook of Product Graphs, 2nd edn. CRC Press, Boca Raton (2011)

    MATH  Google Scholar 

  5. Hsu, W.-J.: Fibonacci cubes—a new interconnection technology. IEEE Trans. Parallel Distrib. Syst. 4, 3–12 (1993)

    Article  Google Scholar 

  6. Jha, P.K., Slutzki, G.: Convex-expansions algorithms for recognition and isometric embedding of median graphs. Ars Comb. 34, 75–92 (1992)

    MATH  MathSciNet  Google Scholar 

  7. Klavžar, S.: On median nature and enumerative properties of Fibonacci-like cubes. Discrete Math. 299, 145–153 (2005)

    Article  MATH  MathSciNet  Google Scholar 

  8. Klavžar, S.: Structure of Fibonacci cubes: a survey. J. Comb. Optim. 25, 505–522 (2013)

    Article  MATH  MathSciNet  Google Scholar 

  9. Klavžar, S., Mollard, M., Petkovšek, M.: The degree sequence of Fibonacci and Lucas cubes. Discrete Math. 311, 1310–1322 (2011)

    Article  MATH  MathSciNet  Google Scholar 

  10. Munarini, E., Perelli Cippo, C., Zagaglia Salvi, N.: On the Lucas cubes. Fibonacci Q. 39, 12–21 (2001)

    MATH  MathSciNet  Google Scholar 

  11. Taranenko, A., Vesel, A.: Fast recognition of Fibonacci cubes. Algorithmica 49, 81–93 (2007)

    Article  MATH  MathSciNet  Google Scholar 

  12. Winkler, P.: Isometric embeddings in products of complete graphs. Discrete Appl. Math. 7, 221–225 (1984)

    Article  MATH  MathSciNet  Google Scholar 

Download references

Acknowledgements

The work is supported by the Ministry of Science of Slovenia under the grant 0101-P-297.

Author information

Authors and Affiliations

  1. Faculty of Natural Sciences and Mathematics, University of Maribor, Maribor, Slovenia

    Aleksander Vesel

Authors
  1. Aleksander Vesel
    View author publications

    You can also search for this author inPubMed Google Scholar

Corresponding author

Correspondence to Aleksander Vesel.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Vesel, A. Linear Recognition and Embedding of Fibonacci Cubes. Algorithmica 71, 1021–1034 (2015). https://doi.org/10.1007/s00453-013-9839-3

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00453-013-9839-3

Keywords