Nearly Constant Tile Complexity for any Shape in Two-Handed Tile Assembly

Abstract

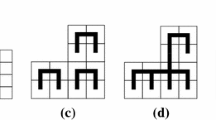
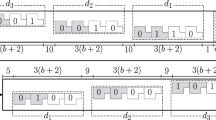
Tile self-assembly is a well-studied theoretical model of geometric computation based on nanoscale DNA-based molecular systems. Here, we study the two-handed tile self-assembly model or 2HAM at general temperatures, in contrast with prior study limited to small constant temperatures, leading to surprising results. We obtain constructions at larger (i.e., hotter) temperatures that disprove prior conjectures and break well-known bounds for low-temperature systems via new methods of temperature-encoded information. In particular, for all $n \in \mathbb {N}$, we assemble $n \times n$ squares using $O(2^{\log ^*{n}})$ tile types, thus breaking the well-known information theoretic lower bound of Rothemund and Winfree. Using this construction, we then show how to use the temperature to encode general shapes and construct them at scale with $O(2^{\log ^*{K}})$ tiles, where K denotes the Kolmogorov complexity of the target shape. Following, we refute a long-held conjecture by showing how to use temperature to construct $n \times O(1)$ rectangles using only $O(\log {n}/\log \log {n})$ tile types. We also give two small systems to generate nanorulers of varying length based solely on varying the system temperature. These results constitute the first real demonstration of the power of high temperature systems for tile assembly in the 2HAM. This leads to several directions for future explorations which we discuss in the conclusion.