Flexible Resource Allocation to Interval Jobs

Abstract

Motivated by the cloud computing paradigm, and by key optimization problems in all-optical networks, we study two variants of the classic job interval scheduling problem, where a reusable resource is allocated to competing job intervals in a flexible manner. Each job, $J_i$, requires the use of up to $r_{max}(i)$ units of the resource, with a profit of $p_i \ge 1$ accrued for each allocated unit. The goal is to feasibly schedule a subset of the jobs so as to maximize the total profit. The resource can be allocated either in contiguous or non-contiguous blocks. These problems can be viewed as flexible variants of the well known storage allocation and bandwidth allocation problems. We show that the contiguous version is strongly NP-hard, already for instances where all jobs have the same profit and the same maximum resource requirement. For such instances, we derive the best possible positive result, namely, a polynomial time approximation scheme. We further show that the contiguous variant admits a $(\frac{5}{4}+\varepsilon )$-approximation algorithm, for any fixed $\varepsilon >0$, on instances whose job intervals form a proper interval graph. At the heart of the algorithm lies a non-standard parameterization of the approximation ratio itself, which is of independent interest. For the non-contiguous case, we uncover an interesting relation to the paging problem that leads to a simple $O(n \log n)$ algorithm for uniform profit instances of n jobs. The algorithm is easy to implement and is thus practical.

A Hardness of fsap for Uniform Instances

Proof of Theorem 8:

The reduction is from of the 3-Exact-Cover (3XC) problem defined as follows. Given a universal set $U=\{e_1,\ldots ,e_{3n}\}$ and a collection $S=\{S_1,\ldots ,S_m\}$ of 3 element subsets of U, is there a sub-collection $S' \subseteq S$ such that each element of U occurs in exactly one member of $S'$. Note that $|S'|=n$, if such exists. Recall that Karp showed in his seminal paper [19] that 3XC is NP-Complete.

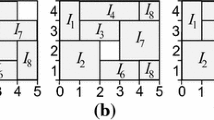
To simplify the presentation, we first assume that the intervals have different profits per allocated unit. For the reduction, we use several sets of intervals. One such set is shown in Fig. 2. It consists of 16 intervals whose lengths and relative positions are given in the figure. Assume that the profit of each of the intervals $9,\ldots ,16$ is higher than the sum of the profits of intervals $1,\ldots ,8$, and that the profit of each of the intervals 2 to 7 is higher than the profit of intervals 1 and 8.

Fig. 2

The “two-choice” set of intervals

Suppose that we are given two “banks” of contiguous colors to allocate to this set of intervals: one bank consists of four contiguous colors and one consists of three contiguous colors. Given that $r_{max}(i)=3$, our first priority is to allocate three colors to each interval in [9..16]. Assuming that three colors are indeed allocated to each interval in [9..16], note that any other interval can be allocated at most one color. This is since any other interval intersects two intervals from [9..16] at a point.

We say that two intervals from [1..8] conflict if both cannot be allocated colors simultaneously. Note that two such intervals conflict if both intersect two intervals from [9..16] at the same time point because only 7 colors are available. Define the conflict graph to be a graph over the vertices [1..8], where two vertices are connected if the respective intervals conflict. It is easy to see that the conflict graph is the path 1–5–2–6–3–7–4–8. Since the profit of intervals [2..7] is higher than the profit of intervals 1 and 8, the best strategy is to allocate one color to three of the intervals in [2..7] and one color to either interval 1 or 8. The only two possibilities for allocating the two banks of colors in such a way are illustrated in Fig. 3. Because of this property, we call this set of intervals a “two-choice” gadget. Note that, in the first option, the bank of 3 colors is unassigned at times: 5, 9 and 13, while in the second option, it is unassigned at times 3, 7 and 11.

Fig. 3

Two possibilities for allocating the two banks of colors

We need to define also a pair of intervals called an “overlapping” pair of intervals, illustrated in Fig. 4. Note that to be able to allocate 3 colors to both intervals, we need one bank of 3 contiguous colors at time interval $[t_1,t_2+1)$ and another at time interval $[t_2,t_3)$; that is, we need both banks at time interval $[t_2,t_2+1)$.

Fig. 4

Overlapping intervals

We now describe the reduction from the 3XC problem. For each set $S_i \in S$, associate a “two-choice” gadget. The “two choices” correspond to the decision whether to include $S_i$ in the cover or not. For each element $e \in U$, and for each set $S_i$ such that $e \in S_i$, we associate a pair of overlapping intervals, where the overlap is in one of the times in which the “two choice” gadget corresponding to set $S_i$ has an unassigned bank of 3 colors. In addition, we define some extra intervals as detailed below.

Given a 3XC problem instance, set $W=9m+7$ and $r_{max}=3$ for all intervals. Let $P=8n+45m$. In the reduction, we have 5 groups of intervals defined as follows.

• (i) Left border: $3m+3$ intervals $L_1,\ldots , L_{3m+3}$ each of profit $P^2$. For $i \in [1..3n]$, $L_i= [0, i)$, for $i \in [3n+1..3m]$, $L_i = [0,4n)$, and for $i \in [3m+1..3m+3]$, $L_i = [0,4n+15m)$.

• (ii) Right border: $3m+3$ intervals $R_1,\ldots R_{3m+3}$ each of profit $P^2$. For $i \in [1..3n]$, $R_i= [5n+45m+i, 8n+45m+1)$, for $i \in [3n+1..3m]$, $R_i = [4n+45m, 8n+45m+1)$, and for $i \in [3m+1..3m+3]$, $R_i = [4n+30m, 8n+45m+1)$.

• (iii) “two choice” gadgets: m copies of the “two choice” gadget, one for each set $S_i \in S$. The gadget associated with set $S_i$ starts at time $4n+15m+15(i-1)$ and its length is 15 time units. The profit of intervals 1 and 8 in each copy is 1, the profit of intervals 2 to 7 is 2, and the profit of intervals 9 to 16 is $P^2$.

• (iv) element overlapping pairs: 3m overlapping pairs of intervals, one per occurrence of an element in a set. For each $S_i \in S$, let $S_i = \{e_a,e_b,e_c\}$, where $\{a,b,c\} \subseteq [1..3n]$. The respective three overlapping pairs are (1) $[a,4n+15m+15(i-1)+3)$ and $[4n+15m+15(i-1)+2,5n+45m+a)$, (2) $[b,4n+15m+15(i-1)+7)$ and $[4n+15m+15(i-1)+6,5n+45m+b)$, and (3) $[c,4n+15m+15(i-1)+11)$ and $[4n+15m+15(i-1)+10,5n+45m+c)$. The profit of each such interval is its length. Note that the profit of any pair of overlapping intervals is $5n+45m+1$.

• (v) “filler” overlapping pairs: 3m overlapping pairs, three per set. For each $S_i \in S$, the respective three overlapping pairs are (1) $[4n,4n+15m+15(i-1)+5)$ and $[4n+15m+15(i-1)+4,4n+45m)$, (2) $[4n,4n+15m+15(i-1)+9)$ and $[4n+15m+15(i-1)+8,4n+45m)$, and (3) $[4n,4n+15m+15(i-1)+13)$ and $[4n+15m+15(i-1)+12,4n+45m)$. The profit of each such interval is its length. Note that the profit of any pair of overlapping intervals is $45m+1$.

$\square$

Lemma 13

The 3XC instance has an exact cover if and only if the associated fsap instance has profit $(18m+14+24m)P^2+7m+9n(5n+45m+1)+(9m-9n)(45m+1)= (42m+14)P^2+405m^2+45n^2+16m$.

Proof

Assume that the 3XC instance has an exact cover. We show an assignment of the intervals in the fsap instance that achieves the desired profit. First, assign color 1 to $L_{3m+2}$ and $R_{3m+2}$ and colors 2, 3, 4 to $L_{3m+3}$ and $R_{3m+3}$. Also assign colors 5, 6, 7 to $L_{3m+1}$ and colors $9m+5,9m+6,9m+7$ to $R_{3m+1}$. Now, consider $S_i$, for $i \in [1..m]$. Assume that $0\le k <i$ sets $S_j$, for $j<i$ are in the cover. (See also Fig. 5.)

Fig. 5

Assigning intervals related to $S_i$

If $S_i$ is not in the cover choose the first option for the “two choice” gadget associated with $S_i$. Namely, assign colors [1..4] to intervals [1..4] and [9..12] in the gadget, and for $j \in [13..16]$ assign colors $9i+3j-43,9i+3j-42,9i+3j-41$ to interval j. Also, assign colors $9i-4,9i-3,9i-2$ to $R_{3(n+i-k)-2}$; for $j \in \{2,3\}$, assign colors $9i+3j-7,9i+3j-6,9i+3j-5$ to $L_{3(n+i-k)+j-4}$ and $R_{3(n+i-k)+j-3}$, and assign colors $9i+5,9i+6,9i+7$ to $L_{3(n+i-k)}$. Finally, assign 3 colors to the 3 “filler” overlapping pairs corresponding to $S_i$ as follows: colors $9i-4,9i-3,9i-2$ to interval $[4n+15m+15(i-1)+4,4n+45m)$, colors $9i-1,9i,9i+1$ to intervals $[4n,4n+15m+15(i-1)+5)$ and $[4n+15m+15(i-1)+8,4n+45m)$, colors $9i+2,9i+3,9i+4$ to intervals $[4n,4n+15m+15(i-1)+9)$ and $[4n+15m+15(i-1)+12,4n+45m)$, and colors $9i+5,9i+6,9i+7$ to interval $[4n,4n+15m+15(i-1)+13)$.

Suppose that $S_i$ is in the cover. Let $S_i = \{e_a,e_b,e_c\}$, where $\{a,b,c\} \subseteq [1..3n]$. Choose the second option for the “two choice” gadget associated with $S_i$. Namely, assign colors [1..4] to intervals [5..8] and [13..16] in the gadget, and for $j \in [9..12]$ assign colors $9i+3j-31,9i+3j-30,9i+3j-29$ to interval j. The respective element overlapping pairs and the border intervals are assigned colors as follows: colors $9i-4,9i-3,9i-2$ to $[4n+15m+15(i-1)+2,5n+45m+a)$ and $R_a$, colors $9i-1,9i,9i+1$ to $L_a$, $[a,4n+15m+15(i-1)+3)$, $[4n+15m+15(i-1)+6,5n+45m+b)$ and $R_b$, colors $9i+2,9i+3,9i+4$ to $L_b$, $[b,4n+15m+15(i-1)+7)$, $[4n+15m+15(i-1)+10,5n+45m+c)$ and $R_c$, and colors $9i+5,9i+6,9i+7$ to $L_c$ and $[c,4n+15m+15(i-1)+11)$.

Note that the assignment is valid, that is, no two overlapping intervals are assigned the same color. To calculate the total profit of the assignment note that $L_{3m+1}, L_{3m+3}, R_{3m+1}$ and $R_{3m+3}$ are each assigned 3 colors and $L_{3m+2}, R_{3m+2}$ are assigned a single color. This contributes $14P^2$ to the profit. Also, intervals [9..16] in all the “two choice” gadgets are assigned 3 colors, and either intervals [1..4] or [5..8] are assigned a single color. This contributes $24mP^2+7m$ to the profit. Since we start from a cover, all the element overlapping pairs as well as the corresponding left and right border intervals are assigned 3 colors each. This contributes $3\cdot 6nP^2+3 \cdot 3n(5n+45m+1)$ to the profit. Since the cover is exact, $3m-3n$ “filler” overlapping pairs as well as the corresponding left and right border intervals are assigned 3 colors each. This contributes $3(6m-6n)P^2+3(3m-3n)(45m+1)$ to the profit. Overall, the profit is $(42m+14)P^2+405m^2+45n^2+16m$.

We now prove the other direction. Suppose that we find an assignment of colors to intervals with total profit $(42m+14)P^2+405m^2+45n^2+16m$. The only way to get total profit of at least $(42m+14)P^2$ is by assigning 3 colors to all intervals with $P^2$ profit per allocated unit in the “two choice” gadgets, and in addition, by assigning 3 colors to all but one left (and right) border intervals, and by assigning the 1 remaining color to the remaining left (and right) border interval.

Consider the (element and “filler”) overlapping pairs. At most 3m left (and right) intervals out of these overlapping pairs can be assigned 3 colors each, since any additional assignment would conflict with the assignment of colors to the border intervals. Out of these 3m left and right intervals, at most 3n left (and right) intervals can be element overlapping intervals.

Since all intervals with $P^2$ profit per allocated unit in the “two choice” gadgets are assigned 3 colors, there are 3m remaining 3 color blocks throughout the interval $[4n+15m,4n+30m)$ and at most one more block of 3 colors is available in each of the 6m time units when some of the intervals with $P^2$ profit per allocated unit in the “two choice” gadgets are not assigned any color (see Fig. 3). The maximum profit that can be attained by assigning these colors to the unassigned intervals in the “two choice” gadgets is at most $3\cdot (2\cdot 6 +2)m= 42m$. Thus the only way to achieve the $405m^2$ term in the profit (for large enough m) is by actually assigning 3 colors to 3m left and 3m right intervals out of the overlapping pairs.

Consider the 3m left intervals of the overlapping pairs that are assigned 3 colors in increasing length order and the right intervals of the overlapping pairs that are assigned 3 colors in decreasing length order. Denote these two sequences by $O^L_1,\dots ,O^L_{3m}$ and $O^R_1,\dots ,O^R_{3m}$.

Claim 2

For $i \in [1..3m]$, if $O^L_i$ and $O^R_i$ overlap, they cannot overlap by more than one time unit.

Proof

Suppose the claim does not hold, and let i be the minimum index for which $O^L_i$ and $O^R_i$ overlap by more than one time unit. However, in this case $O^L_i$ and $O^R_i$ must overlap in at least one time unit t when the intervals with $P^2$ profit per allocated unit in the “two choice” gadgets are assigned two blocks of 3 colors. Since $O^R_i$ contains time t, t is contained also in $O^R_1,\ldots ,O^R_{i-1}$. Similarly, since $O^L_i$ contains time t, t is contained also in $O^L_{i+1},\ldots ,O^L_{3m}$. But this implies that $3m+1$ intervals out of the overlapping pairs and 2 intervals from the “two choice” gadget are each assigned 3 colors. This is impossible, since there are only $9m+7$ colors. $\square$

From the discussion above, it follows that if $O^L_i$ and $O^R_i$ overlap they must be an overlapping pair. The maximum profit that can be attained from the intervals in the “two choice” gadgets that do not have $P^2$ profit per allocated unit is 14m. Thus, to achieve the additional $405m^2+45n^2$ terms in the profit, we must have that for all $i \in [1..3m]$, intervals $O^L_i$ and $O^R_i$ are an overlapping pair, and 3n out of these overlapping pairs are element overlapping pairs. This will contribute $405m^2+45n^2+9m$ to the profit. The extra 7m profit needs to be attained by assigning colors to the intervals in the “two choice” gadgets that do not have $P^2$ profit per allocated unit. It follows that each “two choice” gadget needs to be colored using one of the two options described above and exactly n of them have to be colored using the second option. These n gadgets correspond to the exact cover. $\square$

Finally, we note how the reduction can be modified to include only intervals of identical profit per allocated unit. The idea is to “slice” each interval in the original reduction to smaller intervals whose number is the profit per allocated unit of the original interval. When doing so, we need to ensure that it is not beneficial to move from a “slice” of one interval to a “slice” of another interval. This is done by assigning different displacements to the slices in different intervals, so that whenever we attempt to gain from a move from a “slice” of one interval to a “slice” of another interval, we lose at least one slice due to the different displacements. Thus, the same set of colors will be used for all slices associated with the original interval. This completes the proof of the theorem. $\square$