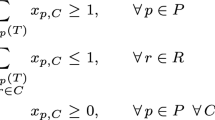Polynomial-time Combinatorial Algorithm for General Max–Min Fair Allocation

Abstract

In the general max–min fair allocation problem, there are m players and n indivisible resources, each player has his/her own utilities for the resources, and the goal is to find an assignment that maximizes the minimum total utility of resources assigned to a player. The problem finds many natural applications such as bandwidth distribution in telecom networks, processor allocation in computational grids, and even public-sector decision making. We introduce an over-estimation strategy to design approximation algorithms for this problem. When all utilities are positive, we obtain an approximation ratio of $\frac{c}{1-\epsilon }$, where c is the maximum ratio of the largest utility to the smallest utility of any resource. When some utilities are zero, we obtain an approximation ratio of $\bigl (1+3{\hat{c}}+O(\delta {\hat{c}}^2)\bigr )$, where ${\hat{c}}$ is the maximum ratio of the largest utility to the smallest positive utility of any resource.

Appendix A: Proof of Lemma 4

We give a proof by contradiction. Suppose to the contrary that $z_{\ell +1}=|{{\mathcal {A}}}_{\ell +1}| < 2\mu |{{\mathcal {B}}}_{\le \ell }|$.

For every $p \in P$, a configuration C for p is a subset of resources (fat or thin) such that p is interested in the resources in C and $v_p(C) \ge 1$. Let ${{\mathcal {C}}}_p(1)$ denote the set of all such configurations for p. The LP relaxation below is the configuration LP for the general max–min allocation problem.

Primal                     Min   0

$$\begin{aligned}\begin{array}{rlrclll} \mathbf{s.t.} &{}&{} \displaystyle \sum _{C\in {{{\mathcal {C}}}_p(1)}}x_{p,C} &{} \ge &{} 1 , &{}~~~~&{} \forall p \in P, \\ &{}&{} \displaystyle \sum _{p\in P}\sum _{r\in C}x_{p,C}&{} \le &{} 1, &{} &{} \forall r\in R, \\ &{}&{} x_{p,C} &{} \ge &{} 0, &{} &{} \forall p \in P, \,\, \forall C \in {{\mathcal {C}}}_p(1). \\ \end{array} \end{aligned}$$

Dual                     Max $\displaystyle \quad \sum _{p \in P}y_p - \sum _{r \in R}z_r$

$$\begin{aligned}\begin{array}{rlrclll} \mathbf{s.t.} &{}&{} \displaystyle y_p &{} \le &{} \displaystyle \sum _{r \in C}z_r, &{} ~~~~ &{} \forall p \in P, \,\, \forall C\in {{\mathcal {C}}}_p(1) \\ &{}&{} y_p &{} \ge &{} 0, &{} &{} \forall p \in P, \\ &{}&{} z_r &{} \ge &{} 0, &{} &{} \forall r \in R. \\ \end{array} \end{aligned}$$

We will define a solution for the dual of configuration LP and show that it is feasible and gives a positive objective function value. We can then scale up this feasible dual solution arbitrarily, which gives an arbitrarily large objective function value. Therefore, the dual of the configuration LP is unbounded, which implies the contradiction that the configuration LP is infeasible. Our proof is largely the same as the counterpart of Lemma 4 in [10, 11], but adaptions to our setting is needed in defining the dual solution and in proving that the objective function value is positive.

To define the dual solution, we need to classify certain subsets of players and resources. Consider the moment right after the completion of the construction of the layer $L_{\ell +1}$.

Let $\Pi$ be a maximum set of node-disjoint paths in $G_M$ from $B_{\le \ell }$ to $A_{\ell +1} \cup I$. Let $src (\Pi )$ denote the set of sources of the paths in $\Pi$. It is possible that the sets $B_{\le \ell }$ and $A_{\ell +1} \cup I$ share some common player, in which case $\Pi$ may contain a path that consists of a single node. We call such a path a trivial path. Other paths in $\Pi$ are non-trivial paths. Let $\Pi ^+$ be the set of non-trivial paths in $\Pi$, i.e., paths with at least one edge. Let $src ({\Pi ^+})$ denote the set of sources of the paths in $\Pi ^+$. The non-trivial paths in $\Pi$ are alternating, that is, for $i \ge 0$, every $(2i+2)$-th edge belongs to M and every $(2i+1)$-th edge does not.

If we flip the alternating paths in $\Pi$, M is updated to another maximum matching of G. Let $M \oplus \Pi$ denote the resulting maximum matching. Note that flipping a trivial path in $\Pi$ does not change anything. The players in $src ({\Pi ^+})$ are not matched in M, but they are now matched in $M \oplus \Pi$, which means that there are directed edges in $G_{M \oplus \Pi }$ from fat resources to the players in $src (\Pi ^+)$. So players in $src (\Pi ^+)$ have in-degree exactly one in $G_{M\oplus \Pi }$.

Let ${P^+}$ be the set of players that can be reached in $G_{M \oplus \Pi }$ from $B_{\le \ell }{\setminus } src (\Pi )$. Let ${R^+_f}$ be the set of fat resources that can be reached in $G_{M \oplus \Pi }$ from $B_{\le \ell }{\setminus } src (\Pi )$. Let ${R^+_t}$ be the set of inactive thin resources. We can now define the desired dual solution $(\{y_p^*\}_{p \in P},\{z_r^*\}_{r \in R})$ as follows:

$$\begin{aligned} y_p^*={\left\{ \begin{array}{ll} \ 1-(1+\gamma )\lambda &{} \text {if }p \in P^+,\\ \ 0 &{} \text {otherwise}. \end{array}\right. } \\ z_r^*={\left\{ \begin{array}{ll} \ 1-(1+\gamma )\lambda &{} \text {if }r \in R^+_f,\\ \ v_r^{\textrm{max}} &{} \text {if } r \in R^+_t,\\ \ 0 &{} \text {otherwise}. \end{array}\right. } \end{aligned}$$

We will need the following properties of $G_{M\oplus \Pi }$.

Proposition 1

In $G_{M\oplus \Pi }$, the players in $B_{\le \ell } {\setminus } src (\Pi )$ have zero in-degrees, and the fat resources in $R_f^+$ have out-degrees exactly one.

Proof

The players in $B_{\le \ell }$ are matched by thin edges in ${\mathcal {E}}$, so they are not matched by M to fat resources. Hence, players in $B_{\le \ell }$ have in-degree zero in $G_M$. After flipping the paths in $\Pi$, among the players in $B_{\le \ell }$, only those in $src (\Pi )$ may now be matched to fat resources in $M \oplus \Pi$, and therefore, players in $B_{\le \ell } {\setminus } src (\Pi )$ are still unmatched in $M \oplus \Pi$. So players in $B_{\le \ell } {\setminus } src (\Pi )$ have zero in-degrees.

By the definition of $R_f^+$, for every resource $r \in R_f^+$, there is a path to r in $G_{M \oplus \Pi }$ from a player in $B_{\le \ell } \setminus src (\Pi )$. If r is not matched in $M \oplus \Pi$, we can flip this path to increase the matching size, contradicting the fact that $M\oplus \Pi$ is a maximum matching. So r is matched in $M\oplus \Pi$, implying that its out-degree in $G_{M\oplus \Pi }$ is exactly one. $\square$

Note that the rest of the proof considers the moment right after completing the construction of $L_{\ell +1}$, and there is no more $(1+\gamma )\lambda$-minimal addable edge that can be discovered.

1.1 A.1 Feasibility

We first prove that the dual solution is feasible, which requires us to show that $y_p^* \le \sum _{r \in C} z_r^*$, $\forall p \in P$, $\forall C \in {{\mathcal {C}}}_i(1)$. The feasibility constraint is trivially satisfied if $p\notin P^+$ because $y_p^* = 0$ in this case and $z_r^* \ge 0$ for all $r \in R$. Take any $p \in P^+$. So $y_p^* = 1 - (1+\gamma )\lambda$ by definition. As $p \in P^+$, there is a path $\pi$ from $B_{\le \ell } {\setminus } src (\Pi )$ to p in $G_{M \oplus \Pi }$. We prove that $\sum _{r \in C} z_r^* \ge 1-(1+\gamma )\lambda$ for all $C \in {{\mathcal {C}}}_p(1)$.

Case 1: C contains a fat resource $r_f$. Since $r_f$ belongs to a configuration for p, p desires r, which means that $G_{M\oplus \Pi }$ contains either the directed edge $(p,r_f)$ or the directed edge $(r_f,p)$. We show that $r_f \in R_f^+$ below. It immediately follows that $z_{r_f}^* = 1 - (1+\gamma )\lambda$, so $\sum _{r \in C} z_r^* \ge z_{r_f}^* = 1 - (1+\gamma )\lambda$.

If $G_{M\oplus \Pi }$ contains the edge $(p,r_f)$, then $r_f \in R_f^+$ because we can follow the path $\pi$ to p and then the edge $(p,r_f)$ to $r_f$. Suppose that $G_{M\oplus \Pi }$ contains the edge $(r_f,p)$. By the property of matching, p has in-degree at most one in $G_{M\oplus \Pi }$, so $(r_f,p)$ is the only edge entering p. It follows that the path $\pi$ reaches $r_f$ first before p, so the prefix of $\pi$ up to $r_f$ certifies that $r_f \in R_f^+$.

Case 2: C contains only thin resources. We consider the moment after completing the construction of $L_{\ell +1}$. Recall that $\Pi$ is a maximum set of node-disjoint paths in $G_M$ from $B_{\le \ell }$ to $A_{\ell +1} \cup I$. The existence of the path $\pi$ in $G_{M \oplus \Pi }$ to p means that there are more than $|\Pi |$ node-disjoint paths in $G_M$ from $B_{\le \ell }$ to $A_{\ell +1} \cup I \cup \{p\}$. Therefore, p is an addable player according to Definition 2. However, we cannot find any $(1+\gamma )\lambda$-minimal addable edge for p upon the completion of $L_{\ell +1}$. Since $C \in {{\mathcal {C}}}_p(1)$, we have $v_p(C) \ge 1$. Therefore, the total utility of active resources in C for p must be less than $(1+\gamma )\lambda$, which means that the total utility of inactive resources in C for p is greater than $1 - (1+\gamma )\lambda$. Since $R_t^+$ is the set of inactive thin resources, we have $\sum _{r \in C} z_r^* \ge \sum _{r \in C \cap R_t^+} z_r^* = \sum _{r \in C \cap R_t^+} v_r^\textrm{max}\ge \sum _{r \cap C \cap R_t^+} v_{p,r} > 1-(1+\gamma )\lambda$.

1.2 A.2 Positive Objective Function Value

By definition, $y_p^* = 0$ if $p \notin P^+$, and $z_r^* = 0$ if $r \notin R_f^+ \cup R_t^+$. So we only need to prove that $\sum _{p \in P^+} y_p^* - \sum _{r \in R_f^+} z_r^* - \sum _{r \in R_t^+} z_r^* > 0$.

First we consider the value of $\sum _{p\in P^+}y_p^* - \sum _{r\in R_f^+} z_r^*$. By definition, $y_p^* = z_r^* = 1-(1+\gamma )\lambda$ for all $p\in P^+$ and $r \in R_f^+$. Then

$$\begin{aligned} \sum _{p \in P^+}y_p^* - \sum _{r\in R_f^+} z_r^* = \Bigl (1-(1+\gamma )\lambda \Bigr )\left( |P^+|-|R_f^+|\right) . \end{aligned}$$

Take any $r \in R_f^+$. By Proposition 1, there is an edge $(r_f,p)$ in $G_{M \oplus \Pi }$ for some player p, i.e., p is matched to $r_f$ in $M\oplus \Pi$. There is a path from $B_{\le \ell } {\setminus } src (\Pi )$ to $r_f$ by the definition of $R_f^+$, which implies that there is a path from $B_{\le \ell } {\setminus } src (\Pi )$ to p. Hence, $p \in P^+$. We can thus charge every $r_f \in R_f^+$ to a player in $P^+$ such that, by the property of matching, no player in $P^+$ is charged more than once. As discussed previously, every player in $B_{\le \ell } {\setminus } src (\Pi )$ is not matched in $M\oplus \Pi$, so players in $B_{\le \ell } \setminus src (\Pi )$ are not charged. Moreover, every player in $B_{\le \ell } {\setminus } src (\Pi )$ belongs to $P^+$ because there is a trivial path from every such player to himself/herself. As a result,

$$\begin{aligned} |P^+|-|R_f^+| \ge |B_{\le \ell }\setminus src (\Pi )|. \end{aligned}$$

Since $\Pi$ is a maximum set of node-disjoint paths in $G_M$ from $B_{\le \ell }$ to $A_{\ell +1} \cup I$, we have $| src (\Pi )| = |\Pi | \le |A_{\ell +1}| + |I|$. Therefore,

$$\begin{aligned} |P^+|-|R_f^+| \ge |B_{\le \ell }\setminus src (\Pi ) | \ge |{{\mathcal {B}}}_{\le \ell }|-|{{\mathcal {A}}}_{\ell +1}|-|{{\mathcal {I}}}|. \end{aligned}$$

We conclude that

$$\begin{aligned} \sum _{p_i \in P^+}y_i^* - \sum _{r_j\in R_f^+} z_j^*= & {} \Bigl (1-(1+\gamma )\lambda \Bigr )\left( |P^+|-|R_f^+|\right) \nonumber \\\ge & {} \Bigl (1-(1+\gamma )\lambda \Bigr ) \Bigl (|{{\mathcal {B}}}_{\le \ell }|-|{{\mathcal {A}}}_{\ell +1}|-|{{\mathcal {I}}}|\Bigr ). \end{aligned}$$

(A.1)

It remains to analyze $\sum _{r \in R_t^+} z_r^*$. Every resource $r \in R_t^*$ is inactive. By definition, the inactive resources appear in three disjoint subsets of thin edges: (i) ${{\mathcal {A}}}_{\le \ell } \cup {{\mathcal {B}}}_{\le \ell }$, (ii) ${{\mathcal {A}}}_{\ell +1} \cup {{\mathcal {I}}}$, and (iii) ${{\mathcal {B}}}'_{\ell +1} = \bigl \{b \in {{\mathcal {B}}}_{\ell +1}: v_\textrm{max}\bigl (R_b \cap R({{\mathcal {A}}}_{\ell +1}) \bigr )> \beta \lambda \bigr \}$. It follows that

$$\begin{aligned} \sum _{r\in R_t^+} z_r^*= & {} \sum _{r \in R_t^+} v_r^{\textrm{max}} \\= & {} v_{\textrm{max}}\bigl (R({{\mathcal {A}}}_{\le \ell } \cup {{\mathcal {B}}}_{\le \ell })\bigr ) + v_{\textrm{max}}\bigl (R({{\mathcal {A}}}_{\ell +1}\cup {{\mathcal {I}}})\bigr ) + v_{\textrm{max}}\bigl (R({{\mathcal {B}}}'_{\ell +1})\bigr ). \end{aligned}$$

We first consider $v_{\textrm{max}}\bigl (R({{\mathcal {A}}}_{\le \ell } \cup {{\mathcal {B}}}_{\le \ell })\bigr )$. Every edge (p, D) in ${{\mathcal {A}}}_{\le \ell }$ is a blocked addable edge. So $v_p\bigl (D {\setminus } R({{\mathcal {B}}}_{\le \ell })\bigr ) < \lambda$. Every edge in ${{\mathcal {B}}}_{\le \ell }$ is $\lambda$-minimal. Thus, we can use the over-estimate strategy to bound $v_\textrm{max}\bigl (R({{\mathcal {A}}}_{\le \ell } \cup {{\mathcal {B}}}_{\le \ell })\bigr )$:

$$\begin{aligned} v_{\textrm{max}}(R({{\mathcal {A}}}_{\le \ell } \cup {{\mathcal {B}}}_{\le \ell })){} & {} \le \sum _{(p,D)\in {{\mathcal {A}}}_{\le \ell } \cup {{\mathcal {B}}}_{\le \ell }} {\hat{c}} \cdot v_p(D) \nonumber \\ [.5em]\le & {} {\hat{c}} \cdot \lambda |{{\mathcal {A}}}_{\le \ell }| + {\hat{c}} \cdot 2\lambda |{{\mathcal {B}}}_{\le \ell }| \nonumber \\{} & {} \mathop {<}\limits ^{\textrm{Lemma}~2} \left( 3+\frac{\beta }{\gamma }\right) {\hat{c}}\cdot \lambda |{{\mathcal {B}}}_{\le \ell }|. \end{aligned}$$

(A.2)

We analyze $v_\textrm{max}\bigl (R({{\mathcal {A}}}_{\ell +1}\cup {\mathcal {I}})\bigr )$ next. Every edge in ${{\mathcal {A}}}_{\ell +1}$ is $(1+\gamma )\lambda$-minimal, and every edge in ${\mathcal {I}}$ is $\lambda$-minimal. Therefore,

$$\begin{aligned} v_{\textrm{max}}\bigl (R({{\mathcal {A}}}_{\ell +1}\cup {\mathcal {I}})\bigr )\le & {} \sum _{(p,D)\in {{\mathcal {A}}}_{\ell +1}\cup {{\mathcal {I}}}} {\hat{c}} \cdot v_p(D) \nonumber \\\le & {} (2+\gamma ) {\hat{c}} \cdot \lambda |{{\mathcal {A}}}_{\ell +1}| + 2{\hat{c}} \cdot \lambda |{\mathcal {I}}|. \end{aligned}$$

(A.3)

Lastly, consider $v_{\textrm{max}}\bigl (R({{\mathcal {B}}}'_{\ell +1})\bigr )$. Edges in ${{\mathcal {B}}}'_{\ell +1}$ are $\lambda$-minimal. Therefore,

$$\begin{aligned} v_{\textrm{max}}\bigl (R({{\mathcal {B}}}'_{\ell +1})\bigr ){} & {} \le \sum _{(p,D)\in {{\mathcal {B}}}'_{\ell +1}} {\hat{c}} \cdot v_p(D) \nonumber \\{} & {} \le 2{\hat{c}} \cdot \lambda |{{\mathcal {B}}}'_{\ell +1}| \nonumber \\{} & {} \mathop {<}\limits ^{\textrm{Lemma} ~3} \left( \frac{4+2\gamma }{\beta }\right) {\hat{c}}^2 \cdot \lambda |{{\mathcal {A}}}_{\ell +1}|. \end{aligned}$$

(A.4)

Summing (A.2), (A.3)) and (A.4) gives

$$\begin{aligned} \sum _{r\in R_t^+} z_r^* < \left( 3+\frac{\beta }{\gamma }\right) {\hat{c}}\lambda |{{\mathcal {B}}}_{\le \ell }| + \left( (2+\gamma ){\hat{c}} + \left( \frac{4+2\gamma }{\beta }\right) {\hat{c}}^2\right) \lambda |{{\mathcal {A}}}_{\ell +1}| + 2{\hat{c}}\lambda |{\mathcal {I}}|.\nonumber \\ \end{aligned}$$

(A.5)

Combining (A.1) and (A.5) gives

$$\begin{aligned}{} & {} \sum _{p\in P^+}y_p^* - \sum _{r\in R_f^+} z_r^* - \sum _{r\in R_t^+} z_r^* \nonumber \\{} & {} \quad > \left( 1 - (1 + \gamma )\lambda - \left( 3 + \frac{\beta }{\gamma }\right) {\hat{c}}\lambda \right) |{{\mathcal {B}}}_{\le \ell }| \nonumber \\{} & {} \qquad - \left( 1 - (1+\gamma )\lambda + (2+\gamma ){\hat{c}}\lambda + \left( \frac{4+2\gamma }{\beta }\right) {\hat{c}}^2\lambda \right) |{{\mathcal {A}}}_{\ell +1}| \nonumber \\{} & {} \qquad - \bigl (1 - (1+\gamma )\lambda + 2{\hat{c}}\lambda \bigr )|{{\mathcal {I}}}|. \end{aligned}$$

(A.6)

We claim that $|{{\mathcal {I}}}| \le \mu |{{\mathcal {B}}}_{\le \ell }|$ because no layer is collapsible. If $|{{\mathcal {I}}}| > \mu |{{\mathcal {B}}}_{\le \ell }|$, there would be some ${{\mathcal {I}}}_i$ in the disjoint partition $\bigcup _{i=1}^\ell {{\mathcal {I}}}_i$ of ${\mathcal {I}}$ such that $|{{\mathcal {I}}}_i| > \mu |{{\mathcal {B}}}_i|$. Note that $|{{\mathcal {I}}}_i| = |I_i|$ because $I_i$ consists of the destinations of node-disjoint paths from ${{\mathcal {B}}}_i$ to ${{\mathcal {I}}}_i$. Also, $|{{\mathcal {B}}}_i| = |B_i|$ because edges in ${{\mathcal {B}}}_i$ belong to a matching of the hypergraph H, so no two edges in ${{\mathcal {B}}}_i$ are incident to the same player. By definition, $f_M[B_{\le i},I] - f_M[B_{\le i-1},I] = |I_i| > \mu |B_i|$. But then the layer $L_i$ is collapsible according to Definition 4, a contradiction to the assumption that no layer is collapsible. This proves our claim.

We have assumed to the contrary of Lemma 4 that $|{{\mathcal {A}}}_{\ell +1}| \le 2\mu |{{\mathcal {B}}}_{\le \ell }|$.

Plugging $\beta = \gamma ^2$, $\mu = \gamma ^3$, and the two inequalities above into (A.6) gives

$$\begin{aligned}{} & {} \sum _{p \in P^+}y_i^* - \sum _{r\in R_f^+} z_r^* - \sum _{r\in R_t^+} z_r^* \\{} & {} \quad > \bigl (1-3\gamma ^3\bigr ) |{{\mathcal {B}}}_{\le \ell }| - \bigl (1 + \gamma - 3\gamma ^3 - 3\gamma ^4\bigr )\lambda |{{\mathcal {B}}}_{\le \ell }| - \bigl (3+\gamma + 6\gamma ^3 + 2\gamma ^4){\hat{c}}\lambda |{{\mathcal {B}}}_{\le \ell }| \\{} & {} \qquad - \bigl (8\gamma +4\gamma ^2){\hat{c}}^2\lambda |{{\mathcal {B}}}_{\le \ell }|. \end{aligned}$$

One can set $\gamma = \Theta (\delta )$ so that

$$\begin{aligned}{} & {} \frac{1-3\gamma ^3}{(1+\gamma -3\gamma ^3-3\gamma ^4)+(3+\gamma +6\gamma ^3+2\gamma ^4){\hat{c}}+(8\gamma +4\gamma ^2){\hat{c}}^2} \\{} & {} \quad > \frac{1}{1+3{\hat{c}}+O(\delta {\hat{c}}^2)} \\{} & {} \quad = \lambda , \end{aligned}$$

which implies that the objective function value is positive.