Tverberg Partitions of Points on the Moment Curve

Abstract

Define $M^d=\{ z(t):t \in \mathbb {R}\}$, where $z(t)=(t,t^2,\ldots ,t^d)\in \mathbb {R}^d$. Suppose $A=\{z(t_i):1\le i\le n\}\subset M^d$, where $t_1<t_2<\cdots <t_n$.

• (a) We show that the set A is “usually” in “strong general position” (SGP).

• (b) The alternating r-partition of A is $(A_1,A_2,\ldots ,A_r)$, where

  

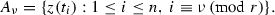
  We observe that if $r=2$ and $n \ge d+2$, then ${{\mathrm{conv}}}A_1 \cap {{\mathrm{conv}}}A_2 \ne \emptyset$ (i.e., $(A_1,A_2)$ is a Radon partition of A). For $r \ge 3$ we show that if $n \ge T(d,r)(=(d+1)(r-1)+1)$, then $\bigcap \nolimits _{\nu =1}^r {{\mathrm{conv}}}A_\nu \ne \emptyset$, provided the numbers $t_1,t_2,\ldots ,t_n$ are chosen “sufficiently far”.

• (c) As a consequence, if

  $$\begin{aligned} n \ge L(d,r,k)=T(d,k)+ (r-k) \big \lceil \tfrac{T(d,k)}{k}\big \rceil , (r \ge 2, \,2 \le k \le \min (d,r-1)), \end{aligned}$$

  and the numbers $t_1,t_2,\ldots ,t_n$ are chosen sufficiently far, then the alternating r-partition of A is an (r, k)-partition, i.e., each k of the sets ${{\mathrm{conv}}}A_\nu$ ($1 \le \nu \le r$) have a point in common. (L(d, r, k) is the smallest n such that a set of n points in SGP in $\mathbb {R}^d$ may admit an (r, k)-partition.)

In this paper we investigate some relationships among three notions: strong general position, Tverberg’s theorem and the moment curve.