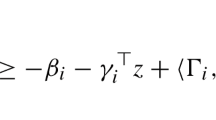Skip to main content
Springer Nature Link
Log in

Complements of Unbounded Convex Polyhedra as Polynomial Images of \({{\mathbb {R}}}^n\)

  • Published:
Discrete & Computational Geometry Aims and scope Submit manuscript

Abstract

We prove constructively that: The complement\({{\mathbb {R}}}^n{\setminus }\mathcal {K}\)of ann-dimensional unbounded convex polyhedron\(\mathcal {K}\subset {{\mathbb {R}}}^n\)and the complement\({{\mathbb {R}}}^n{\setminus }{\text {Int}}(\mathcal {K})\)of its interior are polynomial images of\({{\mathbb {R}}}^n\)whenever\(\mathcal {K}\)does not disconnect\({{\mathbb {R}}}^n\). The case of a compact convex polyhedron and the case of convex polyhedra of small dimension were approached by the authors in previous works. The techniques here are more sophisticated than those corresponding to the compact case and require rational separation results for tuples of variables, which have interest by their own and can be applied to separate certain types of (non-compact) semialgebraic sets.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8

Similar content being viewed by others

References

  1. Acquistapace, F., Andradas, C., Broglia, F.: Separation of semialgebraic sets. J. Am. Math. Soc. 12(3), 703–728 (1999)

    Article  MathSciNet  MATH  Google Scholar 

  2. Basu, S., Pollack, R., Roy, M.-F.: Algorithms in Real Algebraic Geometry. Algorithms and Computation in Mathematics, vol. 10, 2nd edn. Springer, Berlin (2006)

    Book  MATH  Google Scholar 

  3. Berger, M.: Geometry I & II. Universitext. Springer, Berlin (1987)

    Book  Google Scholar 

  4. Bing, R.H.: Generalizations of two theorems of Janiszewski. Bull. Am. Math. Soc. 51(12), 954–960 (1945)

    Article  MathSciNet  MATH  Google Scholar 

  5. Bochnak, J., Coste, M., Roy, M.F.: Real Algebraic Geometry. Ergebnisse der Mathematik und ihrer Grenzgebiete, vol. 36. Springer, Berlin (1998)

    Google Scholar 

  6. Eisenbud, D.: Open problems in computational algebraic geometry. In: Eisenbud, D., Robbiano, L. (eds.) Computational Algebraic Geometry and Commutative Algebra. Symposia Mathematica, vol. 34, pp. 49–70. Cambridge University Press, Cambridge (1993)

    Google Scholar 

  7. Fawzi, H.: On polyhedral approximations of the positive semidefinite cone. arXiv:1811.09649 (2018)

  8. Fernando, J.F.: On the one dimensional polynomial and regular images of \({\mathbb{R}}^n\). J. Pure Appl. Algebra 218(9), 1745–1753 (2014)

    Article  MathSciNet  MATH  Google Scholar 

  9. Fernando, J.F.: On Nash images of Euclidean spaces. Adv. Math. 331, 627–719 (2018)

    Article  MathSciNet  MATH  Google Scholar 

  10. Fernando, J.F., Fichou, G., Quarez, R., Ueno, C.: On regulous and regular images of Euclidean spaces. Q. J. Math. 69(4), 1327–1351 (2018)

    MathSciNet  MATH  Google Scholar 

  11. Fernando, J.F., Gamboa, J.M.: Polynomial images of \({\mathbb{R}}^n\). J. Pure Appl. Algebra 179(3), 241–254 (2003)

    Article  MathSciNet  MATH  Google Scholar 

  12. Fernando, J.F., Gamboa, J.M.: Polynomial and regular images of \({\mathbb{R}}^n\). Israel J. Math. 153, 61–92 (2006)

    Article  MathSciNet  MATH  Google Scholar 

  13. Fernando, J.F., Gamboa, J.M., Ueno, C.: On convex polyhedra as regular images of \({\mathbb{R}}^n\). Proc. Lond. Math. Soc. 103(5), 847–878 (2011)

    Article  MathSciNet  MATH  Google Scholar 

  14. Fernando, J.F., Gamboa, J.M., Ueno, C.: The open quadrant problem: a topological proof. In: A Mathematical Tribute to Professor José María Montesinos Amilibia. Dep. Geom. Topol. Fac. Cien. Mat., pp. 337–350. UCM, Madrid (2016)

  15. Fernando, J.F., Gamboa, J.M., Ueno, C.: Polynomial, regular and Nash images of Euclidean spaces. In: Broglia, F., et al. (eds.) Ordered Algebraic Structures and Related Topics. Contemporary Mathematics, vol. 697, pp. 145–167. American Mathematical Society, Providence (2017)

    Chapter  Google Scholar 

  16. Fernando, J.F., Gamboa, J.M., Ueno, C.: Unbounded convex polyhedra as polynomial images of Euclidean spaces. Ann. Sc. Norm. Super. Pisa Cl. Sci. 19(2), 509–565 (2019)

    Google Scholar 

  17. Fernando, J.F., Ueno, C.: On the set of points at infinity of a polynomial image of \({\mathbb{R}}^n\). Discrete Comput. Geom. 52(4), 583–611 (2014)

    Article  MathSciNet  MATH  Google Scholar 

  18. Fernando, J.F., Ueno, C.: On complements of convex polyhedra as polynomial and regular images of \({\mathbb{R}}^n\). Int. Math. Res. Not. IMRN 2014(18), 5084–5123 (2014)

    Article  MATH  Google Scholar 

  19. Fernando, J.F., Ueno, C.: On the complements of 3-dimensional convex polyhedra as polynomial images of \({\mathbb{R}}^3\). Int. J. Math. 25(7), 1450071 (2014)

    Article  MATH  Google Scholar 

  20. Fernando, J.F., Ueno, C.: A short proof for the open quadrant problem. J. Symb. Comput. 79(1), 57–64 (2017)

    Article  MathSciNet  MATH  Google Scholar 

  21. Föllmer, H., Schied, A.: Stochastic Finance: An Introduction in Discrete Time. de Gruyter Studies in Mathematics, vol. 27, 2nd edn. de Gruyter, Berlin (2004)

    Book  MATH  Google Scholar 

  22. Gamboa, J.M.: Reelle Algebraische Geometrie. June, 10th–16th. Oberwolfach (1990)

  23. González-López, M.J., Recio, T., Santos, F.: Parametrization of semialgebraic sets. Math. Comput. Simul. 42(4–6), 353–362 (1996)

    Article  MathSciNet  Google Scholar 

  24. Handelman, D.: Representing polynomials by positive linear functions on compact convex polyhedra. Pac. J. Math. 132(1), 35–62 (1988)

    Article  MathSciNet  MATH  Google Scholar 

  25. Janiszewski, Z.: Sur les coupures du plan faites par les continus. Prace Mat.-Fiz. 26, 11–63 (1913)

    Google Scholar 

  26. Kubjas, K., Parrilo, P.A., Sturmfels, B.: How to flatten a soccer ball. In: Conca, A., Gubeladze, J., Römer, T. (eds.) Homological and Computational Methods in Commutative Algebra. Springer INdAM Series, vol. 20, pp. 141–162. Springer, Cham (2017)

    Chapter  Google Scholar 

  27. Nie, J., Demmel, J., Sturmfels, B.: Minimizing polynomials via sum of squares over the gradient ideal. Math. Program. 106(3), 587–606 (2006)

    Article  MathSciNet  MATH  Google Scholar 

  28. Parrilo, P.A., Sturmfels, B.: Minimizing polynomial functions. In: Basu, S., Gonzalez-Vega, L. (eds.) Algorithmic and Quantitative Real Algebraic Geometry. DIMACS Series in Discrete Mathematics and Theoretical Computer Science, vol. 60, pp. 83–99. American Mathematical Society, Providence (2003)

    Chapter  Google Scholar 

  29. Rockafellar, T.R.: Convex Analysis. Princeton Mathematical Series, vol. 28. Princeton University Press, Princeton (1970)

    Google Scholar 

  30. Schweighofer, M.: Global optimization of polynomials using gradient tentacles and sums of squares. SIAM J. Optim. 17(3), 920–942 (2006)

    Article  MathSciNet  MATH  Google Scholar 

  31. Stengle, G.: A Nullstellensatz and a Positivstellensatz in semialgebraic geometry. Math. Ann. 207, 87–97 (1974)

    Article  MathSciNet  MATH  Google Scholar 

  32. Ueno, C.: A note on boundaries of open polynomial images of \({\mathbb{R}}^2\). Rev. Mat. Iberoam. 24(3), 981–988 (2008)

    Article  MathSciNet  MATH  Google Scholar 

  33. Ueno, C.: On convex polygons and their complements as images of regular and polynomial maps of \({\mathbb{R}}^2\). J. Pure Appl. Algebra 216(11), 2436–2448 (2012)

    Article  MathSciNet  MATH  Google Scholar 

  34. Vui, Hà Huy, So’n, Phạm Tiên: Global optimization of polynomials using the truncated tangency variety and sums of squares. SIAM J. Optim. 19(2), 941–951 (2008)

    Article  MathSciNet  MATH  Google Scholar 

  35. Yannakakis, M.: Expressing combinatorial optimization problems by linear programs. J. Comput. Syst. Sci. 43(3), 441–466 (1991)

    Article  MathSciNet  MATH  Google Scholar 

  36. Ziegler, G.M.: Lectures on Polytopes. Graduate Texts in Mathematics, vol. 152. Springer, New York (1995)

    Book  Google Scholar 

Download references

Acknowledgements

The authors are strongly indebted with the anonymous referees for their suggestions that have helped them to improve significantly the final version of this article.

Author information

Authors and Affiliations

  1. Departamento de Álgebra, Geometría y Topología, Facultad de Ciencias Matemáticas, Universidad Complutense de Madrid, 28040, Madrid, Spain

    José F. Fernando

  2. Matematika Munkaközösség, Pécsi Kodály Zoltán Gimnázium, Dobó István utca 35-37, Pécs, 7629, Hungary

    Carlos Ueno

Authors
  1. José F. Fernando
    View author publications

    You can also search for this author inPubMed Google Scholar

  2. Carlos Ueno
    View author publications

    You can also search for this author inPubMed Google Scholar

Corresponding author

Correspondence to José F. Fernando.

Additional information

Editor in Charge: Kenneth Clarkson

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

The first author (J.F. Fernando) is supported by Spanish GRAYAS MTM2014-55565-P, Spanish STRANO MTM2017-82105-P and Grupos UCM 910444, whereas the second author (C. Ueno) is an external collaborator of the first two grants. This work was also partially supported by the “National Group for Algebraic and Geometric Structures and their Applications” (GNSAGA - INdAM). This article was partially written during a common one year research stay of the authors in the Dipartimento di Matematica of the Università di Pisa. The authors would like to thank the department for the invitation and the very pleasant working conditions. The one year research stay of the first author was partially supported by MECD grant PRX14/00016. The one year research stay of the second author was mainly supported by ‘Scuola Galileo Galilei’ Research Grant at the Dipartimento di Matematica of the Università di Pisa (D.R. n\(^{\text {o}}\)27519 of 29/07/2013, MAT/03).

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Fernando, J.F., Ueno, C. Complements of Unbounded Convex Polyhedra as Polynomial Images of \({{\mathbb {R}}}^n\). Discrete Comput Geom 62, 292–347 (2019). https://doi.org/10.1007/s00454-019-00065-2

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00454-019-00065-2

Keywords

Mathematics Subject Classification