The Maximum Size Of Graphs With A Uniquek- Factor

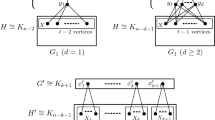
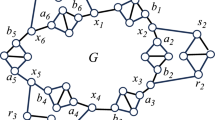
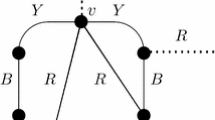
For suitable positive integers n and k let m(n, k) denote the maximum number of edges in a graph of order n which has a unique k-factor. In 1964, Hetyei and in 1984, Hendry proved $m{\left( {n,1} \right)} = \frac{{n^{2} }} {4}$ for even n and $m{\left( {n,2} \right)} = {\left\lfloor {\frac{{n{\left( {n + 1} \right)}}} {4}} \right\rfloor }$, respectively. Recently, Johann confirmed the following conjectures of Hendry: $m{\left( {n,k} \right)} = \frac{{nk}} {2} + {\left( {{}^{{n - k}}_{2} } \right)}$ for$k > \frac{n} {2}$ and kn even and $m{\left( {n,k} \right)} = \frac{{n^{2} }} {4} + {\left( {k - 1} \right)}\frac{n} {4}$ for n = 2kq, where q is a positive integer. In this paper we prove $m{\left( {n,k} \right)} = k^{2} + {\left( {{}^{{n - k}}_{2} } \right)}$ for $\frac{n} {3} \leqslant k < \frac{n} {2}$ and kn even, and we determine m(n, 3).