How Balanced Can Permutations Be?

Abstract

A permutation $\pi \in \mathbb {S}_n$ is k-balanced if every permutation of order k occurs in $\pi$ equally often, through order-isomorphism. In this paper, we explicitly construct k-balanced permutations for $k \le 3$, and every n that satisfies the necessary divisibility conditions. In contrast, we prove that for $k \ge 4$, no such permutations exist. In fact, we show that in the case $k \ge 4$, every n-element permutation is at least $\Omega _n(n^{k-1})$ far from being k-balanced. This lower bound is matched for $k=4$, by a construction based on the Erdős–Szekeres permutation.

1 Introduction

A permutation $\tau \in \mathbb {S}_k$ occurs as a pattern in $\pi \in \mathbb {S}_n$, if there are indices $1\le s_1< \dots < s_k\le n$ such that

$$\begin{aligned} \forall i,j \in \{1, \dots , k\}:\ \pi (s_i)< \pi (s_j) \iff \tau (i) < \tau (j). \end{aligned}$$

This simple concept of order-isomorphism gives rise to many intriguing problems.

The local structure of permutations. The k-profile of an n-element permutation $\pi$ is the vector that counts the occurrences of every order-k pattern in $\pi$. There are still many things we do not know about the set of k!-dimensional vectors that arise in this way. The Erdős–Szekeres Theorem [8] states that every order-n permutation must contain a monotone pattern of order $\lceil \sqrt{n}~\rceil$. Conversely, the packing density of a pattern $\tau \in \mathbb {S}_k$ is its maximal proportion within the k-profile of an n-element permutation, as $n \rightarrow \infty$. Packing densities have received considerable attention [1, 26, 28], yet even for $\mathbb {S}_4$ some answers remain presently unknown. Patterns in random permutations have also received their share of attention [9, 15], as has the algorithmic problem of computing the k-profile [7, 10]. Both are relevant to certain basic questions in mathematical statistics. Every one of the above questions also has a graph-theoretic analogue. For instance, the counterpart to Erdős–Szekeres ’ Theorem is Ramsey’s Theorem, and the graph-theoretic equivalent to packing density is inducibility [24], and so forth.

1.1 Our Contribution

In this paper we consider the permutation-theoretic analogue of combinatorial designs. For integers $n \ge k \ge 1$, we say that a permutation $\pi \in \mathbb {S}_n$ is k-balanced if every order-k pattern occurs in $\pi$ equally often, i.e. exactly $\left( {\begin{array}{c}n\\ k\end{array}}\right) /k!$ times. By way of example, $\pi = \texttt{2413}$ is 2-balanced. So, for which values of n and k does there exist a k-balanced permutation $\pi \in \mathbb {S}_{n}$? We answer this question fully.

Constructions for $k \le 3$. It is not hard to see that any k-balanced permutation is $(k-1)$-balanced (see Sect. 2.1). Therefore, for an n-element permutation to be k-balanced, we must at least have $r! \mid \left( {\begin{array}{c}n\\ r\end{array}}\right)$, for every $r \le k$. It is a straightforward exercise to see that these necessary divisibility conditions suffice in the case $k=2$, that is, 2-balanced permutations exist for every admissible n. Is the same true for $k=3$? Our first result answers this in the positive, resolving an open question of [6].

Theorem 1

For $k\le 3$ and every n, there exists a k-balanced permutation in $\mathbb {S}_n$ iff n is admissible.

Our construction for $k=3$ is explicit and relies heavily on rotation-invariance (see Sect. 3). The divisibility conditions for 3-balanced permutations permit six remainders in $\mathbb {Z}/36\mathbb {Z}$, and we provide infinite families corresponding to each. These families are all based on a single basic construction, and together cover all but a spurious collection of 19 admissible values of n, which we handle individually.

Theorem 1 proves the existence of 3-balanced “designs”. This has many noteworthy counterparts. For example, a (r, s; n)-Steiner system is a collection of r-element subsets of $\{1, 2, \dots , n\}$, such that every s-element subset is contained in the same number of members in the system. Such a system can exist only if n, r and s satisfy certain arithmetic conditions, and a major discovery of Keevash [17] (see also [11]) says that for fixed $r>s>1$ and for large enough n, if the above arithmetic conditions are satisfied, then a Steiner system exists. Similarly, in graph theory, Janson and Spencer [16] considered proportional graphs, in which every subgraph of a fixed size appears the exact number of times it is expected to appear. They showed that with respect to order-3 subgraphs, there exist infinitely many proportional graphs. Finally, with regards to permutations, Cooper and Petrarca [6] noted the existence of 3-balanced permutations for $n=9$ (the least admissible n), and our Theorem 1 extends this to every admissible n.

Our proof of Theorem 1 is related to rotational symmetries of the square. We consider rotation-invariant permutations, and give a simple characterisation of them. The construction of 3-balanced permutations then follows by fixing a rotation-invariant “outer structure”, and reducing the problem to finding a smaller permutation that, when planted within the “inner structure”, will satisfy the balancedness condition. Enforcing rotational symmetries means we need only balance the number of occurrences of patterns within the two orbits of the action of $D_4$ on $\mathbb {S}_3$. The inner structure permutations are constructed as parametric families, one for every admissible moduli defined by the divisibility conditions of 3-balanced permutations.

Non-existence for $k \ge 4$. For our second result, we prove that there are no 4-balanced permutations. As the k-balanced condition is downwards closed in k, we obtain the following.

Theorem 2

There are no k-balanced permutations for $k\ge 4$.

The proof of Theorem 2 follows by establishing a simple polynomial identity relating entries of the r-profile of any permutation, for $r \le 4$ (see Sect. 4). The 4-balanced profile violates this identity. This resolves another open question of [6], who carried out a large (non-exhaustive) computer search for $n=64$, the smallest admissible 4-balanced cardinality. This explains why none were found.

Theorem 2 is closely related to a result of Naves, Pikhurko and Scott [21], who proved the non-existence of proportional graphs, in which every order-4 subgraph appears exactly the expected number of times. Their proof similarly relies on a polynomial identity. Our result is also related to quasirandom permutations, i.e., infinite families in which the normalised k-profile converges asymptotically to uniform, as n tends to infinity. The theory of graph limits and graphons [19] has been highly influential in graph theory in recent years, and an analogous theory concerning limits of permutations and the notion of permutons has been investigated as well, e.g., [5, 12, 13]. Notions of pseudo-random graphs were introduced by Thomason [27] and a remarkable result of Chung, Graham and Wilson [4] shows that a graph is pseudo-random iff it has the “right” number of 4-cycles. Proving a conjecture of R. Graham (see [5]), Kràl’ and Pikhurko [18] proved that a permuton is quasirandom iff it is 4-symmetric. Our techniques in proving Theorem 2 differ from those of [18], and we point out the difficulty in applying the latter to the discrete setting in Sect. 4.3.

Minimum distance from k-balanced. If (as we show) k-balanced permutations do not exist for $k \ge 4$, how close to balanced can they be? Formally, we define the distance of $\pi \in \mathbb {S}_n$ from being k-balanced, to be the $\ell _\infty$-distance between $\pi$’s k-profile and the uniform vector $(\left( {\begin{array}{c}n\\ k\end{array}}\right) /k!)\mathbb {1}$. We prove:

Theorem 3

For $k\ge 4$, the distance of every n-element permutation from being k-balanced is $\Omega _n(n^{k-1})$.

Our proof of Theorem 3 can be viewed as a robust version of our proof of Theorem 2, using the same polynomial identity (see Sect. 5). We prove that the bound in Theorem 3 is tight for $k = 4$. That is, we give a construction of permutations that attain this distance, asymptotically. This construction is based on a modification of the well-known Erdős–Szekeres permutation [8]. In order to argue about the pattern counts in the 4-profile of our new family of permutations, we use a polynomial method.

For larger k the tightness of our bound remains open. However, we note that all entries in the k-profile of a uniformly random permutation in $\mathbb {S}_n$ are, with probability $>99\%$ (for large enough n), within distance $\Theta _n(n^{k - 1/2})$ from $\left( {\begin{array}{c}n\\ k\end{array}}\right) /k!$ (see Sect. 5.3). So, in the remaining cases, our bound is at most $\mathcal {O}_n\left( \sqrt{n}\right)$-far¹ from tight.

Relation between profiles and permutations. Our last result is of a slightly different flavour, and is of interest only when $k=k(n)$ grows with n. Given a k-profile we seek properties which are common to all n-element permutations that have this profile.

Theorem 4

There exists a set of $\widetilde{\Omega }(k^2/n)$ points in the $[n] \times [n]$ grid, such that the points of any two n-element permutations with the same k-profile coincide in their restriction to this set.

Our proof of Theorem 4 is established by drawing a connection between polynomials and k-profiles (see Sect. 6). First, we introduce a notion of evaluating a bivariate polynomial on a permutation. We then show that fixing the k-profile of a permutation uniquely determines the evaluations of all bivariate polynomials of degree $<k$ on it. This then allows us to use results from approximation theory, in particular, we construct low-degree $\ell _1$-approximations of the point-indicator functions on the grid. The degree of the approximants is related to its distance from the boundary of the grid, and this in turn defines the set of points fixed by the k-profile.

Open questions There remain many interesting questions. For instance, is the distance lower bound tight? And for how many patterns simultaneously? We refer the reader to the discussion in Sect. 7.

2 Preliminaries

As usual, we denote the symmetric group on n elements by $\mathbb {S}_n$. By default we write permutations in $\mathbb {S}_n$ in the one-line notation, and think of a permutation as a bijection from [n] to itself, where $[n] {:}{=}\{1, 2, \dots , n\}$. Any finite set of points in the plane, no two of which are axis-aligned, defines a permutation. Let $\mathcal {A} = \{ (x_1, y_1), (x_2, y_2), \dots , (x_n, y_n) \} \subset \mathbb {R}^2$ be a set of points, where $x_1<\ldots <x_n$ and all $y_i$ are distinct. Then, corresponding to $\mathcal {A}$ is the permutation $\sigma \in \mathbb {S}_n$ (denoted $\mathcal {A} \cong \sigma$), where $y_{\sigma ^{-1}(1)}< y_{\sigma ^{-1}(2)}< \dots < y_{\sigma ^{-1}(n)}$.

The order-isomorphism of permutations is the focus of our work.

Definition 2.1

(order-isomorphism). Let $\pi \in \mathbb {S}_n$ and $\tau \in \mathbb {S}_k$ be permutations, where $k \le n$. Let $S = \{s_1, \dots , s_k\} \subseteq [n]$, where $s_1< \dots < s_k$. We say that $\pi$ induced on S is order-isomorphic to $\tau$ if

$$\begin{aligned} \forall i,j \in [k]:\ \pi (s_i)< \pi (s_j) \iff \tau (i) < \tau (j), \end{aligned}$$

and we denote this condition by $\pi (S) \cong \tau$. When this is the case, we say the pattern $\tau$ occurs in $\pi$. The number of occurrences of $\tau$ in $\pi$ is denoted by ${\# \mathtt { \tau } \left( \pi \right) }$, i.e.:

$$\begin{aligned} {\# \mathtt { \tau } \left( \pi \right) } {:}{=}\Big | \Big \{ S \in \left( {\begin{array}{c}[n]\\ k\end{array}}\right) \ :\ \pi (S) \cong \tau \Big \} \Big |. \end{aligned}$$

Thus, e.g., ${\# \texttt{ 123 } \left( \pi \right) }$ indicates the number of ascending triples in $\pi$. We also define:

Definition 2.2

(k-profile of a permutation). Let $\pi \in \mathbb {S}_n$ be a permutation and let $1 \le k \le n$ be an integer. The k-profile of $\pi$ is defined as follows:

$$\begin{aligned} \mathcal {P}_k(\pi ) {:}{=}\big ( {\# \mathtt { \tau } \left( \pi \right) } \big )_{\tau \in \mathbb {S}_k} \in \mathbb {R}_{\ge 0}^{\mathbb {S}_k}. \end{aligned}$$

This is a vector of $|\mathbb {S}_k|=k!$ non-negative integers that sum to $\left( {\begin{array}{c}n\\ k\end{array}}\right)$.

This brings us to our main object of study.

Definition 2.3

(k-balanced permutation). We say that a permutation $\pi \in \mathbb {S}_n$ is k-balanced for some $1 \le k \le n$ if:

$$\begin{aligned} \forall \tau \in \mathbb {S}_k:\ {\# \mathtt { \tau } \left( \pi \right) } = \frac{\left( {\begin{array}{c}n\\ k\end{array}}\right) }{k!}. \end{aligned}$$

2.1 Basic Observations on Balanced Permutations

We first observe that the k-profile of a permutation uniquely determines its r-profile for every $r<k$, and in particular every k-balanced permutation is also r-balanced.

Proposition 2.4

(downward induction of pattern distribution). Let $n>k>r$ be positive integers. If $\pi \in \mathbb {S}_n$ and $\tau \in \mathbb {S}_{r}$, then

$$\begin{aligned} \left( {\begin{array}{c}n-r\\ k-r\end{array}}\right) \cdot {\# \mathtt { \tau } \left( \pi \right) } = \sum _{\sigma \in \mathbb {S}_k} {\# \mathtt { \tau } \left( \sigma \right) } \cdot {\# \mathtt { \sigma } \left( \pi \right) }. \end{aligned}$$

(1)

Proof Consider the pairs $B\subset A\subset [n]$ where $|B|=r$, $|A|=k$ and $\pi (B) \cong \tau$. The r.h.s. expression is obtained by grouping together in this count all sets A with $\pi (A) \cong \sigma$, for every permutation $\sigma \in \mathbb {S}_{k}$. For the l.h.s., note that for every $B\subset [n]$ with $\pi (B) \cong \tau$, there are exactly $\left( {\begin{array}{c}n-r\\ k-r\end{array}}\right)$ sets A with $B\subset A\subset [n]$. $\square$

Corollary 2.5

(k-balanced implies $(<k)$-balanced). For $n>k>r$, every k-balanced permutation $\pi \in \mathbb {S}_n$ is also r-balanced.

Proof By a simple inductive argument it suffices to consider the case $r=k-1$. So, fix some $\tau \in \mathbb {S}_{k-1}$ and notice that the sum $\sum _{\sigma \in \mathbb {S}_k} {\# \mathtt { \tau } \left( \sigma \right) }$ does not depend on $\pi$. Indeed, to evaluate this sum, think of $\tau$ as an ordering of the integers in $[k-1]$, and view an occurrence of $\tau$ in some $\sigma \in \mathbb {S}_k$ as that ordering in which exactly one of the numbers $\{j-\frac{1}{2} : j=1,\ldots ,k\}$ is inserted somewhere. This perspective yields $\sum _{\sigma \in \mathbb {S}_k} {\# \mathtt { \tau } \left( \sigma \right) }=k^2$, as there are k choices for j as above and k spots at which $j-\frac{1}{2}$ can be inserted. If $\pi$ is k-balanced, then ${\# \mathtt { \sigma } \left( \pi \right) }=\left( {\begin{array}{c}n\\ k\end{array}}\right) /{k!}$, and as claimed, ${\# \mathtt { \tau } \left( \pi \right) }=\left( {\begin{array}{c}n\\ k-1\end{array}}\right) /{(k-1)!}$ by Equation (1). $\square$

Corollary 2.5 yields the following divisibility conditions.

Corollary 2.6

(divisibility conditions for k-balanced permutations). If $\pi \in \mathbb {S}_n$ is k-balanced for some $1 \le k \le n$, then $r! \mid \left( {\begin{array}{c}n\\ r\end{array}}\right)$ for all $1 \le r \le k$.

3 k-Balanced Permutations for $k\le 3$

In this section we show that for $k=2$ and $k=3$, the divisibility conditions of Corollary 2.6 are not only necessary, but also sufficient. Namely, we show that a k-balanced permutation on n elements exists, whenever n satisfies that arithmetic condition. As a warmup, we first describe the case $k=2$.

3.1 2-Balanced Family

The following is one way (of many) to construct such an infinite family.

Proposition 3.1

(2-balanced family). There exists a $2$-balanced permutation in $\mathbb {S}_n$ if and only if $n\equiv 0 \pmod 4$ or $n\equiv 1 \pmod 4$.

Proof For any permutation $\pi \in \mathbb {S}_n$, swapping a pair of adjacent elements in $\pi$ only changes that pair from ascending to descending or vice versa, leaving all other pairs unaffected. So, this increments one of ${\# \texttt{ 12 } \left( \pi \right) }$, ${\# \texttt{ 21 } \left( \pi \right) }$ by one, and decrements the other.

The identity permutation $\pi =(1,2,\dots , n) \in \mathbb {S}_n$ clearly satisfies ${\# \texttt{ 12 } \left( \pi \right) }=\left( {\begin{array}{c}n\\ 2\end{array}}\right)$ and ${\# \texttt{ 21 } \left( \pi \right) }=0$. At the other extreme, the descending permutation $\tau = (n, \dots , 2, 1) \in \mathbb {S}_n$ satisfies ${\# \texttt{ 21 } \left( \tau \right) }=\left( {\begin{array}{c}n\\ 2\end{array}}\right)$ and ${\# \texttt{ 12 } \left( \tau \right) }=0$. It is possible to move from $\pi$ to $\tau$ by a sequence of adjacent swaps (e.g., by “bubble-sorting”). By the discrete intermediate value theorem, if $\left( {\begin{array}{c}n\\ 2\end{array}}\right)$ is even, then there exists an intermediate permutation $\sigma$ satisfying ${\# \texttt{ 12 } \left( \sigma \right) } = {\# \texttt{ 21 } \left( \sigma \right) } = \left( {\begin{array}{c}n\\ 2\end{array}}\right) / 2$. Finally, $\left( {\begin{array}{c}n\\ 2\end{array}}\right)$ is even exactly when n is 0 or $1 \pmod 4$. $\square$

The case $k=2$ is deceptively simple: the plot thickens for larger k, and it is far from the truth that any collection of k! non-negative integers summing up to $\left( {\begin{array}{c}n\\ k\end{array}}\right)$ is a k-profile of some permutation $\pi \in \mathbb {S}_n$. E.g., by the Erdős–Szekeres Theorem [8], we cannot have ${\# \texttt{ 123 } \left( \pi \right) }={\# \texttt{ 321 } \left( \pi \right) }=0$ whenever $n\ge 5$.

3.2 3-Balanced Family

To construct a $3$-balanced family, we take a different approach. Consider the action $D_4 \curvearrowright \mathbb {S}_n$ of the dihedral group on $\mathbb {S}_n$, where we view any permutation $\pi \in \mathbb {S}_n$ as the set of points $\{(i, \pi (i))\}$ in $\mathbb {R}^2$, and act on the square $[1,n]^2$ in the standard way. This group action has the useful property that it respects pattern counts, in the following sense:

Lemma 3.2

(pattern counts under action of $D_4$). Let $\pi \in \mathbb {S}_n$ and $\tau \in \mathbb {S}_k$ be two permutations, and let $g \in D_4$. Then, ${\# \mathtt { \tau } \left( \pi \right) } = {\# \mathtt { g.\tau } \left( g.\pi \right) }$.

Proof Any occurrence of $\tau$ in $\pi$ is associated with a set of points in $[1,n]^2$ where $\tau$ appears. These points are rigidly mapped by g to points at which $g.\tau$ appears, therefore ${\# \mathtt { \tau } \left( \pi \right) } = {\# \mathtt { g.\tau } \left( g.\pi \right) }$. $\square$

Consequently, if the permutation $\pi \in \mathbb {S}_n$ is 3-balanced, then so are all the permutations in $\pi$’s orbit under the action of $D_4$. This orbit may include at most $|D_4| = 8$ permutations. Conversely, for $n > 1$, the orbit must include at least two permutations, since no permutation is identical to its reflections about the horizontal and vertical axes, respectively (they agree on no more than one point).

For any element $g \in D_4$ and permutation $\pi \in \mathbb {S}_n$, we say that $\pi$ is g-invariant if $g.\pi = \pi$ (i.e., g is in the stabiliser of $\pi$). As noted, clearly no permutation is invariant to reflections about either axis. However, rotation-invariant permutations do exist. In other words, $r.\pi = \pi$ where $r \in D_4$ is the $90^\circ$-rotation of the square (therefore, $g.\pi = \pi$ for all $g\in \langle r \rangle$). Rotation-invariant permutations are simply characterised, as follows.

Proposition 3.3

(characterisation of rotation-invariant permutations). Let $n>1$ be even.² Then,

• 1. There exists a rotation-invariant $\pi \in \mathbb {S}_n$ if and only if $n=4m$, for some natural m.

• 2. Let $A \sqcup B = [2m]$ with $|A|=|B|=m$, and let $\sigma :A \rightarrow B$ be a bijection between A and B. To every such A, B and $\sigma$ there corresponds a rotation-invariant permutation in $\mathbb {S}_{4m}$. All rotation-invariant permutations in $\mathbb {S}_{4m}$ are generated in this way.

Proof 1

We start with the second part. Consider the action $\langle r \rangle \curvearrowright [4m]^2$ of $r \in D_4$, the $90^{\circ }$-clockwise rotation. The orbit of a point $(x,y) \in [4m]^2$ is:

$$\begin{aligned} O(x,y) = \{(x, y), (y, 4m-x+1), (4m-x+1, 4m-y+1), (4m-y+1, x)\}. \end{aligned}$$

Let A, B and $\sigma$ be as specified. For every $i \in A$ consider the orbit $O(i, \sigma (i))$ and its projections on the coordinate axes. Note that the four integers $\{i, \sigma (i), 4m-i+1, 4m-\sigma (i)+1\}$ are all distinct. Consequently, all m orbits, $\sqcup _{i \in A} O(i, \sigma (i)) \subseteq [4m]^2$ comprise a set of cardinality 4m with no repeated coordinates, and therefore define a permutation in $\mathbb {S}_{4m}$.

Conversely, suppose $\pi \in \mathbb {S}_{4m}$ is rotation-invariant. The action $\langle r \rangle \curvearrowright [4m]^2$ maps quadrants to quadrants, therefore they must each contain exactly m points. Let $A {:}{=} \{ x : x,\pi (x) \in [2m] \}$ and $B {:}{=} \{ y : \pi ^{-1}(y),y \in [2m] \}$. By the previous argument, we have $\{ (i, \pi (i)) : i \in [4m] \} = \sqcup _{i \in A} O(i, \pi (i))$. As $|A| = m$, every orbit $O(i, \pi (i))$ must have cardinality four, and this holds if and only if $\pi$ is fixed-point-free. Consequently, the sets A and B must be disjoint. The proof now follows by fixing the bijection $\sigma : A \rightarrow B$, where $\sigma (i) {:}{=}\pi (i)$ for all $i \in A$.

Since the rotation action maps quadrants to quadrants, the number of points in a rotation-invariant permutation is necessarily divisible by 4, so the characterisation is complete. $\square$

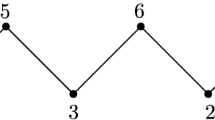
Consider the orbits in $\mathbb {S}_3$ under the action of the $90^\circ$-rotation $r \in D_4$.

Fig. 1

Orbits in $\mathbb {S}_3$ under the action $\langle r \rangle \curvearrowright \mathbb {S}_3$, where $r \in D_4$

Referring to Fig. 1 and Lemma 3.2 yields the following useful fact regarding rotation-invariant permutations.

Lemma 3.4

(3-profile of rotation-invariant permutations). If $\pi \in \mathbb {S}_n$ is rotation-invariant, then:

$$\begin{aligned} {\# \texttt{ 123 } \left( \pi \right) }={\# \texttt{ 321 } \left( \pi \right) }\text { and }{\# \texttt{ 132 } \left( \pi \right) }={\# \texttt{ 231 } \left( \pi \right) }={\# \texttt{ 213 } \left( \pi \right) }={\# \texttt{ 312 } \left( \pi \right) }. \end{aligned}$$

In particular, $\pi$ is $3$-balanced if and only if ${\# \texttt{ 123 } \left( \pi \right) }={\# \texttt{ 132 } \left( \pi \right) }$.

Fig. 2

Plot of the $3$-balanced permutation $\pi = \texttt{761258943} \in \mathbb {S}_9$. By enumeration, the two shortest $3$-balanced permutations are $\pi$ and its inverse (see also [6]). Both are rotation-invariant.$^{2}$

³

Before we proceed to describe our construction, we note the arithmetic implications of Corollary 2.6 on any $3$-balanced permutation.

Lemma 3.5

(divisibility conditions for $3$-balanced permutations). If $\pi \in \mathbb {S}_n$ is $3$-balanced, then $n\equiv 0$, 1, 9, 20, 28, or $29 \pmod {36}$.

3.2.1 A Rotation-Invariant Construction

Lemma 3.4 suggests that we seek rotation-invariant permutations, while Proposition 3.3 provides a recipe for constructing such a permutation in terms of a bipartition and a bijection. By Lemma 3.5, there is a $3$-balanced permutation in $\mathbb {S}_n$ only if $n\equiv 0$ or $1 \pmod {4}$. For our construction, we fix the bipartition $A \sqcup B$ where $A = \{ m + 1, \dots , 2m \}$ and $B=\{1, \dots , m\}$. The planar diagram of $\pi$ in $\mathbb {R}^2$ looks as follows.

Fig. 3

Schematic plot of a rotation-invariant permutation $\pi \in \mathbb {S}_n$, where we fix the bipartition $\{1, \dots , m \} \sqcup \{ m + 1, \dots , 2m \}$ (see Proposition 3.3). When n is odd, we add the blue point at the centre. Here $\pi$ has the “external structure” of $\texttt{3142} \in \mathbb {S}_4$

We now express the pattern counts of $\pi$ in terms of $\sigma$, as follows.

Lemma 3.6

Let $\sigma \in \mathbb {S}_m$, and let $\pi \in \mathbb {S}_n$ be obtained by rotation as in Fig. 3, where $n=4m$. Then:

$$\begin{aligned} {\# \texttt{ 123 } \left( \pi \right) }&= 2\cdot {\# \texttt{ 123 } \left( \sigma \right) } + 2\cdot {\# \texttt{ 321 } \left( \sigma \right) } + 4m\cdot {\# \texttt{ 12 } \left( \sigma \right) }+2m\cdot {\# \texttt{ 21 } \left( \sigma \right) } \\ {\# \texttt{ 132 } \left( \pi \right) }&= {\# \texttt{ 132 } \left( \sigma \right) } + {\# \texttt{ 231 } \left( \sigma \right) } + {\# \texttt{ 213 } \left( \sigma \right) } + {\# \texttt{ 312 } \left( \sigma \right) } + m^3 + m\cdot {\# \texttt{ 12 } \left( \sigma \right) } \\&\quad + 2m\cdot {\# \texttt{ 21 } \left( \sigma \right) }. \end{aligned}$$

In particular, $\pi$ is $3$-balanced if and only if:

$$\begin{aligned} 3\cdot {\# \texttt{ 123 } \left( \sigma \right) }+3\cdot {\# \texttt{ 321 } \left( \sigma \right) }+3m\cdot {\# \texttt{ 12 } \left( \sigma \right) }=\left( {\begin{array}{c}m\\ 3\end{array}}\right) +m^3. \end{aligned}$$

(2)

Proof 2

The expressions are obtained by case analysis. Any occurrence of a pattern $\tau \in \mathbb {S}_3$ in $\pi$ can be composed in three ways: either by taking all three points from the same “block”, or by taking a pair from one block and a single point from another, or by picking one from each (see Fig. 3).

For example, every ascending triplet in $\sigma$ and its $180^\circ$-rotation contributes 1 to ${\# \texttt{ 123 } \left( \pi \right) }$, hence the term $2\cdot {\# \texttt{ 123 } \left( \sigma \right) }$. Similarly, every choice of one element from each of forms a $\texttt{132}$ pattern, hence the $m^3$ term in ${\# \texttt{ 132 } \left( \pi \right) }$. The other terms are obtained similarly. Equaiton (2) now follows by rearranging and substituting the sum of $\sigma$’s 3-profile by $\left( {\begin{array}{c}m\\ 3\end{array}}\right)$. $\square$

To construct an infinite $3$-balanced family, it suffices to find permutations $\sigma \in \mathbb {S}_m$ that satisfy Equaiton (2). Initially, let us consider the following construction. Place three identical descending segments, each of length $\ell \ge 1$, in ascending order. As before, the patterns in $\sigma$ can be counted through case analysis. For example, an ascending pair is formed by choosing two of the three segments, and then one element from each. We obtain:

$$\begin{aligned} {\# \texttt{ 12 } \left( \sigma \right) } = 3 \ell ^2, \qquad {\# \texttt{ 123 } \left( \sigma \right) } = \ell ^3, \qquad {\# \texttt{ 321 } \left( \sigma \right) } = 3 \left( {\begin{array}{c}\ell \\ 3\end{array}}\right) . \end{aligned}$$

These values nearly satisfy Equaiton (2). Indeed, both sides of the equation agree on the cubic and quadratic terms, and disagree only on the linear terms. To achieve equality, we amend the construction slightly, by inserting two additional points “in-between” the existing ones (i.e., placing them at non-integer coordinates). For a parameter $\ell< r < 3\ell /2$ to be chosen below, and a small constant $0< \varepsilon < 1$, the new coordinates are the following (see Fig. 4).

$$\begin{aligned} (x_1,y_1) {:}{=}(r+2+\varepsilon ,r+\ell +\varepsilon ), \qquad (x_2,y_2) {:}{=}(r+\ell +\varepsilon ,r-\varepsilon ). \end{aligned}$$

Fig. 4

Amending the basic construction of $\sigma \in \mathbb {S}_m$ by inserting two points, and fixing $r= \lceil 4\ell / 3 \rceil$

Theorem 5

(3-balanced family). For every $n \ge 9$, there exists a $3$-balanced permutation in $\mathbb {S}_n$ if and only if n satisfies the divisibility conditions. That is, $n\equiv 0$, 1, 9, 20, 28, or $29 \pmod {36}$.

Proof 3

We begin with the case $n \equiv 20 \pmod {36}$. By Lemma 3.6, it suffices to calculate the pattern counts of the amended $\sigma \in \mathbb {S}_m$. Taking into account the two new points, and performing case analysis similarly to the above, we have:

$$\begin{aligned} {\# \texttt{ 12 } \left( \sigma \right) }&= 3 \ell ^2 + (r - 1) + (2\ell -r) + (r + 2) + (2\ell -r) \\ {\# \texttt{ 123 } \left( \sigma \right) }&= \ell ^{3}+(r-\ell -1)\ell +(r-1)(2\ell -r)+(r-\ell +2)\ell +(r+2)(2\ell -r) \\ {\# \texttt{ 321 } \left( \sigma \right) }&= 3 \left( {\begin{array}{c}\ell \\ 3\end{array}}\right) + \left( {\begin{array}{c}2\ell -(r-1)\\ 2\end{array}}\right) + \left( {\begin{array}{c}r-\ell \\ 2\end{array}}\right) + \left( {\begin{array}{c}2\ell -r-2\\ 2\end{array}}\right) \\&\quad + \left( {\begin{array}{c}r-\ell \\ 2\end{array}}\right) + (3\ell - 2r - 1). \end{aligned}$$

Equaiton (2) now simplifies to the condition $r=(4\ell +2)/3$. Therefore, writing $\ell =3t+1$ and $r=4t+2$, we obtain an infinite family of $3$-balanced permutations, for every choice of $t\ge 2$. We have $|\sigma | = m = 3\ell +2=9t+5$ and therefore $|\pi |=n=36t+20$, so this yields a $3$-balanced permutation for every $n > 56$ where $n \equiv 20 \pmod {36}$. The remaining residues (see Lemma 3.5) can be similarly handled, by amending $\sigma$ via a specifically chosen set of points. The details appear in Appendix A. $\square$

Remark 3.7

For n that fails the divisibility conditions, this construction still produces nearly balanced permutations. In particular, letting $\ell =3t$ or $\ell =3t+2$, and taking $r=\lfloor 4\ell /3 \rfloor +1$, the discrepancy in Equaiton (2) is at most $\pm 2$.

4 Non-existence of k-Balanced Permutations for $k \ge 4$

In view of the results in Sect. 3, one may seek k-balanced permutations for $k>3$. In this section we show that no such permutations exist. By the monotonicity proven in Corollary 2.5, it suffices to show that there exist no 4-balanced permutations.

4.1 Warmup: Showing that $k(n) < \log n + (2 + \varepsilon )\log \log n$

For a permutation $\pi \in \mathbb {S}_n$ to be k-balanced, it clearly must have at least $|\mathbb {S}_k|$ k-tuples, i.e., $\left( {\begin{array}{c}n\\ k\end{array}}\right) \ge k!$, which yields by Stirling’s formula $k \lesssim e \sqrt{n}$. In fact, more is true: by Corollary 2.5 the number of r-tuples in $\pi$ must be divisible by r!, for all $r \le k$. This yields the following (see [6] for further discussions of these divisibility conditions).

Proposition 4.1

(ruling out $k \ge \log n + (2 + \varepsilon )\log \log n$). Let $k=k(n)$ be a function and let $\varepsilon > 0$ be a constant. If there exist k(n)-balanced permutations in $\mathbb {S}_n$, then for any sufficiently large n,

$$\begin{aligned} k(n) < \log n + (2 + \varepsilon ) \log \log n. \end{aligned}$$

Proof As usual, we denote by $\nu _2(t)$ the largest integer s for which $2^s \mid t$. Since $k!\mid \left( {\begin{array}{c}n\\ k\end{array}}\right)$,

$$\begin{aligned} \nu _2(k!) \le \nu _2 \left[ \left( {\begin{array}{c}n\\ k\end{array}}\right) \right] = \nu _2(n!) - \nu _2(k!) - \nu _2((n-k)!). \end{aligned}$$

It is a standard fact that $\nu _2(r!)=\sum _{i\ge 1} \lfloor r/2^i\rfloor$. The value of this sum is between r, and $r - \log r - \mathcal {O}(1)$. Consequently $2^k / k^2 = \mathcal {O}(n)$, which implies the proposition. $\square$

Remark 4.2

If we take $n=(k!)^2$, then $r! \mid \left( {\begin{array}{c}n\\ r\end{array}}\right)$ for all $r \in [k]$. It therefore follows that Proposition 4.1 cannot be improved by more than an $\mathcal {O}(\log \log n)$-factor by divisibility alone.

4.2 Non-existence of 4-Balanced Permutations

The following simple lemma provides a polynomial identity relating the $\{2,3,4\}$-profiles of any permutation, by squaring the number of increasing pairs and counting the resulting patterns. It is a direct corollary of this lemma that there exist no 4-balanced permutations. We remark that [21] employs such a technique in graphs, squaring the number of edges and counting the resulting subgraphs.

Lemma 4.3

Every permutation $\pi \in \mathbb {S}_n$ satisfies the following identity:

$$\begin{aligned} \left( {\# \texttt{ 12 } \left( \pi \right) } \right) ^2&=\ 6 \cdot {\# \texttt{ 1234 } \left( \pi \right) } + 4 \cdot {\# \texttt{ 1243 } \left( \pi \right) } + 4 \cdot {\# \texttt{ 1324 } \left( \pi \right) } + 2 \cdot {\# \texttt{ 1342 } \left( \pi \right) } \\&\quad +\ 2 \cdot {\# \texttt{ 1423 } \left( \pi \right) } + 4 \cdot {\# \texttt{ 2134 } \left( \pi \right) } + 4 \cdot {\# \texttt{ 2143 } \left( \pi \right) } + 2 \cdot {\# \texttt{ 2314 } \left( \pi \right) } \\&\quad +\ 2 \cdot {\# \texttt{ 2413 } \left( \pi \right) } + 2 \cdot {\# \texttt{ 3124 } \left( \pi \right) } + 2 \cdot {\# \texttt{ 3142 } \left( \pi \right) } + 2 \cdot {\# \texttt{ 3412 } \left( \pi \right) } \\&\quad +\ 6 \cdot {\# \texttt{ 123 } \left( \pi \right) } + 2 \cdot {\# \texttt{ 132 } \left( \pi \right) } + 2 \cdot {\# \texttt{ 213 } \left( \pi \right) } + {\# \texttt{ 12 } \left( \pi \right) }. \end{aligned}$$

Proof 4

Let us randomly sample independently and uniformly four indices from [n]. We consider the event that the sampled indices form two ascending pairs in $\pi$. By independence,

$$\begin{aligned} \Pr _{i,j,k,l \sim [n]} \left[ i< j,\ \pi (i)< \pi (j),\ k< l,\ \pi (k)< \pi (l) \right]&= \Pr _{i,j \sim [n]} \left[ i< j,\ \pi (i) < \pi (j) \right] ^2 \\&= \left( \frac{{\# \texttt{ 12 } \left( \pi \right) }}{n^2} \right) ^2. \end{aligned}$$

The same event can also be computed as a weighted sum of patterns of $\le 4$ elements, by conditioning over the possible equalities between the sampled indices, and on their ordering. Fixing the set of indices in play and their order uniquely determines the patterns in $\pi$ that contribute to the event above. The computation then follows by total probability. To illustrate this analysis, we briefly analyse the first term in the above identity, leaving the full details to Appendix Appendix B.

Consider the case in which all the indices i, j, k, l are distinct. This event happens with probability $\left( n(n-1)(n-2)(n-3) \right) /n^4$. Conditioned on this event, fix a total order on the indices. As the indices are sampled uniformly at random and there are no ties, each order occurs with probability exactly (1/4!). Under these two conditions, it only remains to enumerate over all patterns $\tau \in \mathbb {S}_4$ satisfying the original event, each of which contributes ${\# \mathtt { \tau } \left( \pi \right) }/\left( {\begin{array}{c}n\\ 4\end{array}}\right)$. For example, if $i< j< k < l$, the corresponding patterns are:

$$\begin{aligned} {\# \texttt{ 1234 } \left( \pi \right) } + {\# \texttt{ 1324 } \left( \pi \right) } + {\# \texttt{ 3412 } \left( \pi \right) } + {\# \texttt{ 2413 } \left( \pi \right) } + {\# \texttt{ 1423 } \left( \pi \right) } + {\# \texttt{ 2314 } \left( \pi \right) }. \end{aligned}$$

and if $i< k< j < l$, we have:

$$\begin{aligned} {\# \texttt{ 1324 } \left( \pi \right) } + {\# \texttt{ 1234 } \left( \pi \right) } + {\# \texttt{ 3142 } \left( \pi \right) } + {\# \texttt{ 2143 } \left( \pi \right) } + {\# \texttt{ 1243 } \left( \pi \right) } + {\# \texttt{ 2134 } \left( \pi \right) }. \end{aligned}$$

The proof is concluded by applying total probability and collecting all terms (see Appendix Appendix B). $\square$

Remark 4.4

The product of permutations appearing in the above lemma, and subsequently throughout Sect. 5, is equivalent to the product defined in Razborov’s Flag Algebra [25], within the context of the theory of permutation patterns and permutons (see e.g. [3]). However, our proof does not involve limit objects (see Sect. 4.3), but rather direct computation of the probabilities therein.

The non-existence of 4-balanced permutations now follows directly.

Theorem 6

There are no 4-balanced permutations.

Proof 5

Arguing by contradiction, suppose that $\pi \in \mathbb {S}_n$ is a 4-balanced permutation. By the monotonicity property of Corollary 2.5, there holds ${\# \mathtt { \tau } \left( \pi \right) } = \left( {\begin{array}{c}n\\ r\end{array}}\right) /r!$ for every $r \le 4$ and every $\tau \in \mathbb {S}_r$. Substituting into the identity of Lemma 4.3, we obtain:

$$\begin{aligned} \left[ \frac{\left( {\begin{array}{c}n\\ 2\end{array}}\right) }{2!}\right] ^2 = \frac{36}{4!} \left( {\begin{array}{c}n\\ 4\end{array}}\right) + \frac{10}{3!} \left( {\begin{array}{c}n\\ 3\end{array}}\right) + \frac{1}{2!} \left( {\begin{array}{c}n\\ 2\end{array}}\right) \end{aligned}$$

(3)

and simplifying yields $n(n-1)(2n + 5) = 0$, a contradiction. $\square$

4.3 Comparison to the Quasirandomness Proof of Kràl’ and Pikhurko

In this paper we examine profiles of permutations and the conditions under which they may be balanced. This is somewhat related to quasirandomness of permutations, and the asymptotic convergence of the k-profile to uniform. Formally,

Definition 4.5

(quasirandom permutations). Let $\Pi = \{ \pi _n \}$ be an infinite family of permutations of non-decreasing order. We say that $\Pi$ is quasirandom if for every $k > 1$ and every $\tau \in \mathbb {S}_k$, we have:

$$\begin{aligned} \frac{{\# \mathtt { \tau } \left( \pi _n \right) }}{\left( {\begin{array}{c}n\\ k\end{array}}\right) } \rightarrow \frac{1}{k!} \ \text {, as } n \rightarrow \infty . \end{aligned}$$

In an influential paper, [18] Kràl’ and Pikhurko proved a conjecture of Graham (see [5]), showing that every asymptotically 4-balanced infinite family of permutations is quasirandom. Namely, if $\Pi$ has the property that ${\# \mathtt { \tau } \left( \pi _n \right) }/\left( {\begin{array}{c}n\\ 4\end{array}}\right) \rightarrow \tfrac{1}{4!}$ (as $n \rightarrow \infty$) for every $\tau \in \mathbb {S}_4$, then $\Pi$ is quasirandom.

Permutons or permutation limits are central to the proof of [18] (see also [12, 13]). A limit object in this framework is a doubly stochastic measure, i.e., a measure with uniform marginals on the unit square $[0,1]^2$. Any such measure $\mu$ gives rise to a sampling process that produces permutations: just pick k points uniformly at random from $\mu$, and consider the corresponding planar pattern. With probability 1 these points define a permutation. Kràl’ and Pikhurko show that, up to sets of measure zero, the Lebesgue measure $\lambda$ is the one and only 4-balanced, doubly stochastic measure on $[0,1]^2$.

Reinterpreting the proof of  [18]. Consider two experiments. In the first, sample a point uniformly from the unit square, then sample two points independently from the measure $\mu$. In the second experiment, we first sample a point uniformly from $[0,1]^2$, then one point from $\mu$, and another point sampled uniformly from the unit square. In both experiments we consider the event that the first sampled point lies to the top-right of the two subsequent points. The success probabilities of these experiments can be expressed in terms of $\mu$ and $\lambda$’s density functions $F,G: [0,1]^2 \rightarrow [0,1]$, respectively, on the bottom-left rectangles of the unit square. Concretely, for all $(a,b) \in [0,1]^2$,

$$\begin{aligned} F(a,b) {:}{=}\mu ([0,a] \times [0,b]), \text { and } G(a,b) {:}{=}\lambda ([0,a] \times [0,b]) = ab. \end{aligned}$$

From here the proof of [18] proceeds by connecting between F, G and the success probabilities of the experiments, which can then be computed using the fact that $\mu$ is 4-balanced. Rather than recount the proof, let us slightly delay the exposition and instead proceed directly to a discrete setting, where it is more convenient to provide full details.

Fig. 5

Two experiments. In the first, we sample a uniform grid point and two points from $\pi$, and consider the event that both $\pi$-points fall to the bottom-left of the initial point. The second experiment starts likewise, but the final point is sampled uniformly. In the continuous setting one cannot distinguish the hybrid distribution from the original one, whereas in the discrete setting this can be done

The discrete setting. To recast [18] in a discrete setting, let us replace the measure $\mu$ with a permutation $\pi \in \mathbb {S}_n$: i.e., rather than sample from $\mu$, now sample points uniformly from $\{(i, \pi (i))\}_{i \in [n]}$. Instead of the two functions F, G on the unit square defined above, we have two functions on the grid, $u,v: [n]^2 \rightarrow [0,1]$, which are defined by:

$$\begin{aligned} \forall x,y \in [n]^2:\ v(x,y) {:}{=}\frac{xy}{n^2}, \text { and } u(x,y) {:}{=}\frac{|\{i \le x:\pi (i) \le y\}| }{n} \end{aligned}$$

Here v is the bottom-left density function of the uniform doubly stochastic matrix $\frac{1}{n} \cdot \mathbb {1} \otimes \mathbb {1}$, and u is the normalised number of points in the bottom-left rectangles of the permutation matrix associated with $\pi$ (i.e., the probability that a point chosen at random from $\pi$ falls in any such rectangle). As before, we would like to compute the probabilities of the events corresponding to the two experiments outlined above. To do so, observe that sampling a uniform point on the grid can be “simulated” by sampling two points independently and uniformly at random from $\{(i, \pi (i))\}_i$, keeping only the x-coordinate from the first point, and the y-coordinate from the second. We can now conduct the two experiments and present their relation to the functions u and v. By total probability, for the first experiment we have:

$$\begin{aligned} \Pr _{i,j,x,y \sim [n]}[i,j \le x \wedge \pi (i),\pi (j) \le \pi (y) ]&= \sum _{s, t \in [n]} \Pr _{x,y \sim [n]}[x=s, \pi (y)=t] \\&\quad \cdot \Pr _{i,j \sim [n]}[i,j \le s \wedge \pi (i),\pi (j) \le t ] \\&= \frac{1}{n^2} \sum _{s,t \in [n]} \Pr _{i \sim [n]}[i \le s \wedge \pi (i) \le t]^2 \\&= \frac{1}{n^2} \sum _{s,t \in [n]} u(s,t)^2 = \frac{1}{n^2} \Vert u \Vert _2^2, \end{aligned}$$

and similarly for the second experiment:

$$\begin{aligned} \Pr _{i,j,k,x,y \sim [n]}[i,j \le x \wedge \pi (i),\pi (k) \le \pi (y) ] = \frac{1}{n^2} \sum _{s,t \in [n]} u(s,t) \cdot v(s,t) = \frac{1}{n^2} \langle u, v \rangle . \end{aligned}$$

Similarly to the proof of Lemma 4.3, these two probabilities can also be directly expressed in terms of weighted sums of permutation patterns in $\pi$, over at most 5 points (in the continuous setting, by applying Cauchy-Schwarz, one can make do with only 4-point patterns).

This is where the proof from the continuous setting no longer carries over to the discrete case: in the continuous setting, both events can be shown to occur with the same probability, exactly $\frac{1}{9}$. Then, since $\Vert G \Vert _2^2 = \frac{1}{9}$, it follows that $\langle F,G \rangle ^2 = \Vert F \Vert _2^2 \Vert G \Vert _2^2$, and by Cauchy-Schwarz, $F = G$ (up to a set of measure zero), and this implies $\mu = \lambda$. In the discrete setting this does not hold. The primary difference being that we must also consider the events in which ties occur, and unlike the continuous setting, these events have non-zero probabilities. Factoring in the possibility of ties and assuming that $\pi$ is a 5-balanced permutation (and thus also 4-balanced, see Corollary 2.5), we obtain the following identities, by a computation similar to the proof of Lemma 4.3:

$$\begin{aligned} \Pr _{i,j,x,y \sim [n]}[i,j \le x \wedge \pi (i),\pi (j) \le \pi (y) ]&= \frac{1}{9} + \frac{13}{36n} + \frac{7}{18n^2} + \frac{5}{36n^3} \\ \Pr _{i,j,k,x,y \sim [n]}[i,j \le x \wedge \pi (i),\pi (k) \le \pi (y) ]&= \frac{1}{9} + \frac{1}{3n} + \frac{13}{36n^2} + \frac{1}{6n^3} + \frac{1}{36n^4} = \frac{\Vert v \Vert _2^2}{n^2}. \end{aligned}$$

While the two probabilities agree on the leading term (which corresponds to the event of no ties), they disagree on the remaining terms. Therefore we cannot apply Cauchy-Schwarz to argue that $u=v$ (which would have indeed yielded a contradiction, since the function u associated with any permutation has exactly n different values, whereas v has $\Theta (n^2)$ different values and therefore does not correspond to any permutation), and must pursue a different proof.

5 The Minimal Distance from k-Balanced for $k \ge 4$

As we just saw, permutations cannot be k-balanced for any $k \ge 4$. But what is the smallest possible distance (in, say, $\ell _\infty$-norm) between an attainable profile and the uniform profile? Here is what we know:

Lower bound. For any $k \ge 4$, we show that the minimal distance from k-balanced is at least $\Omega \left( n^{k-1} \right)$. The proof follows from a robust version of Lemma 4.3, and is given in Sect. 5.1.

Upper bound. For $k=4$, we provide an explicit construction of an infinite family of permutations whose members attain a distance $\mathcal {O}\left( n^3\right)$ from uniform. The construction is based on a modification of the well-known Erdős–Szekeres permutation [8], and is given in Sect. 5.2. Consequently, our bounds on the 4-profile are asymptotically tight to within a constant factor. The remaining cases, where $k > 4$, are presently left open.

Concentration and anti-concentration The asymptotic distribution of the k-profile is a well-researched topic [2, 9, 14, 15]. We observe that these results imply that for any fixed $k \ge 2$, with probability $> 99\%$ the k-profile of a uniformly random $\pi \sim \mathbb {S}_n$ has distance $\Theta (n^{k-1/2})$ from balanced, as $n \rightarrow \infty$. Therefore, if our lower bound for $k \ge 4$ is not tight for any k, then it is off by a multiplicative factor of $\mathcal {O}(n^{1/2})$ (see Sect. 5.3 for a discussion).

5.1 A Lower Bound on the Distance

Notation 5.1

(distance from uniform k-profile). Let $\pi \in \mathbb {S}_n$ be a permutation and let $1 \le k \le n$ be an integer. The distance of $\pi$ from the uniform k-profile, in $\ell _\infty$-norm, is denoted as follows:

$$\begin{aligned} \delta _{\pi ,k} {:}{=}\max _{\tau \in \mathbb {S}_k} \left| {\# \mathtt { \tau } \left( \pi \right) } - \frac{\left( {\begin{array}{c}n\\ k\end{array}}\right) }{k!} \right| . \end{aligned}$$

We also denote the smallest distance over all n-element permutations by $\delta _k(n) {:}{=}\min _{\pi \in \mathbb {S}_n} \delta _{\pi , k}$.

Lemma 5.2

(low-distance k-profile implies low-distance $(k-1)$-profile). For every $\pi \in \mathbb {S}_n$ and $1 < k \le n$:

$$\begin{aligned} \delta _{\pi ,k-1} \le \frac{k^2}{n-k+1} \delta _{\pi ,k}. \end{aligned}$$

Proof 6

Pick some $\pi \in \mathbb {S}_n$ and $\tau \in \mathbb {S}_{k-1}$. Slightly modifying the proof of Equation (1) and Corollary 2.5, we write:

$$\begin{aligned} (n-k+1) \cdot {\# \mathtt { \tau } \left( \pi \right) } & = \sum _{\sigma \in \mathbb {S}_k} {\# \mathtt { \tau } \left( \sigma \right) } \cdot {\# \mathtt { \sigma } \left( \pi \right) } \le \left( \frac{\left( {\begin{array}{c}n\\ k\end{array}}\right) }{k!} + \delta _{\pi ,k} \right) \\ & \quad \sum _{\sigma \in \mathbb {S}_k} {\# \mathtt { \tau } \left( \sigma \right) } = \left( \frac{\left( {\begin{array}{c}n\\ k\end{array}}\right) }{k!} + \delta _{\pi ,k} \right) \cdot k^2. \end{aligned}$$

Therefore,

$$\begin{aligned} {\# \mathtt { \tau } \left( \pi \right) } \le \frac{\left( {\begin{array}{c}n\\ k-1\end{array}}\right) }{(k-1)!} + \frac{k^2}{n-k+1}\cdot \delta _{\pi ,k}. \end{aligned}$$

The lower bound follows similarly. $\square$

Theorem 7

(lower bound on distance from k-balanced). For every constant $k\ge 4$, there holds $\delta _k(n) = \Omega (n^{k-1})$.

Proof 7

In the proof of Lemma 4.3, we derived Equaiton (3) by expressing ${\# \texttt{ 12 } \left( \pi \right) } \cdot {\# \texttt{ 12 } \left( \pi \right) }$ as a combination of pattern counts. To extend this proof to k-profiles, consider the product of ${\# \texttt{ 12 } \left( \pi \right) }$ and ${\# \mathtt { (1,2,\ldots ,k-2) } \left( \pi \right) }$. Fix $k \ge 4$, and suppose toward contradiction that there exists a sequence of permutations $\left\{ \pi _N \right\} _N$, indexed by $N=N(t)$ where $N(t)=\omega _t(1)$, for which $\delta _k(N)/N^{k-1} =o(1)$. By Lemma 5.2, the same permutations also yield $\delta _r(N)/N^{r-1} =o(1)$ for every $1 < r \le k$. In other words, every pattern in the r-profile of $\pi _N$ is $o(N^{r-1})$ away from $\left( {\begin{array}{c}N\\ r\end{array}}\right) /r!$.

As in the proof of Lemma 4.3, we equate between two ways to express the product of pattern counts in $\pi _N$. On the one hand:

$$\begin{aligned}&{\# \texttt{ 12 } \left( \pi _N \right) } \cdot {\# \mathtt { (1,\ldots ,k-2) } \left( \pi _N \right) } = \left( \frac{\left( {\begin{array}{c}N\\ 2\end{array}}\right) }{2!} \pm o(N) \right) \left( \frac{\left( {\begin{array}{c}N\\ k-2\end{array}}\right) }{(k-2)!} \pm o(N^{k-3}) \right) \nonumber \\&= \frac{1}{4(k-2)!^2}\cdot N^k + \frac{-k^2+5k-8}{8(k-2)!^2} \cdot N^{k-1} \pm o(N^{k-1}). \end{aligned}$$

(4)

On the other hand, we express the product as a sum of patterns of lengths k, $k-1$, and $k-2$, obtained from all possible ways in which the two patterns can be combined. In this discussion it is helpful to think of a permutation as an axis-unaligned set of points in the grid. To account for the k-patterns that are generated, consider the insertion of an ascending pair into the permutation $(1,\ldots ,k-2)$. There are $k-1$ possible x-coordinates at which we may insert the first point, and then k for the second point. This counts every pair twice, so there are $k(k-1)/2$ options. The same is true of the y-coordinates, giving $\left( k(k-1)/2\right) ^2$ patterns of length k.

If a $(k-1)$-pattern is formed, necessarily one of the ascending pair’s elements coincides with points of $(1,\ldots ,k-2)$, and the other does not. Suppose the former has coordinates (i, i), for some $1\le i\le k-2$. To insert another element before it, such that an ascending pair is formed, we can freely insert a point among the permutation $(1,\ldots ,i-1)$, and there are $i^2$ ways to choose its coordinates. Similarly, to insert an element to the top-right of (i, i), there are $(k-1-i)^2$ options. Summing these squares over $1\le i\le k-2$ gives $2\cdot (k-2)(k-1)(2k-3)/6$. The remaining case, in which a $(k-2)$-pattern is formed, is negligible in this calculation. Indeed, there are at most $\mathcal {O}(N^{k-2})$ such patterns, each occurring a constant number of times. Overall, we have:

$$\begin{aligned} & \left( \frac{k(k-1)}{2}\right) ^2 \left( \frac{\left( {\begin{array}{c}N\\ k\end{array}}\right) }{k!} \pm o(N^{k-1}) \right) + \frac{2(k-2)(k-1)(2k-3)}{6} \\ & \quad \left( \frac{\left( {\begin{array}{c}N\\ k-1\end{array}}\right) }{(k-1)!} \pm o(N^{k-2}) \right) + \mathcal {O}(N^{k-2}) \end{aligned}$$

and therefore:

$$\begin{aligned}&{\# \texttt{ 12 } \left( \pi _N \right) } \cdot {\# \mathtt { (1,\ldots ,k-2) } \left( \pi _N \right) } = \frac{1}{4(k-2)!^2} \cdot N^k + \frac{-3k^3 +22k^2 -59k+48}{24(k-1)!(k-2)!}\nonumber \\&\quad \cdot N^{k-1} \pm o(N^{k-1}). \end{aligned}$$

(5)

Equaiton (4) and Equaiton (5) agree on their leading terms, but not on the second-order term for any $k \ge 4$. The contradiction follows by taking a sufficiently large N. $\square$

5.2 Matching Upper Bound on the Distance for $k=4$

In this subsection we show that Theorem 7 is asymptotically tight when $k=4$. I.e., there exists an infinite family of permutations, the 4-profiles of which are only $\mathcal {O}(n^{3})$ away from balanced. Our construction is a modification of the classical Erdős–Szekeres permutation [8].

Definition 5.3

(Erdős–Szekeres permutations). For integers $n,m \ge 1$ and $\theta >0$, let $\mathcal {P}(\theta )$ be the set of points in the $[n] \times [m]$ grid, rotated by an angle of $\theta$ about the origin. Let $\delta >0$ be the smallest angle such that some two points in $\mathcal {P}(\delta )$ reside on the same axis-parallel line. Pick some $0<\varepsilon <\delta$. The positive (resp. negative) Erdős–Szekeres permutation, denoted ${{\,\textrm{ES}\,}}^+(n,m)$ (resp. ${{\,\textrm{ES}\,}}^-(n,m)$) is the permutation associated with the point set $\mathcal {P}(\varepsilon )$ (resp. $\mathcal {P}(-\varepsilon )$). When $n=m$, we omit the second operand.

Motivation. In [18] it was shown that for any $k\ge 4$, the unique measure corresponding to a limit permutation with balanced k-profiles is the Lebesgue measure on the unit square. This suggests that in search of permutations with nearly balanced k-profiles, one may consider “square-like” families whose members locally resemble this measure. While the Erdős–Szekeres permutations are natural candidates in this respect, their distance from uniform substantially exceeds the cubic bound.

Proposition 5.4

(Erdős–Szekeres is far from 4-balanced). Let $n > 1$ be an integer and let $\pi = {{\,\textrm{ES}\,}}^+(n)$ be the Erdős–Szekeres permutation over $n^2$ elements. Then ${\# \texttt{ 3142 } \left( \pi \right) } = \left( {\begin{array}{c}n+2\\ 4\end{array}}\right) ^2$, and in particular:

$$\begin{aligned} \delta _{\pi , 4} \ge \frac{1}{144} n^{7} + \mathcal {O}(n^6). \end{aligned}$$

Proof 8

Let $n > 1$, let $\pi = {{\,\textrm{ES}\,}}^+(n)$ and let $\tau = \texttt{3142}$. Let A be the following set of four points, $A = \{(x_1, y_1), (x_2, y_2), (x_3, y_3), (x_4, y_4)\} \subseteq ([n] \times [n])$, whose x-coordinates are in weakly ascending order, $x_1 \le x_2 \le x_3 \le x_4$.

In order for A to form an instance of $\tau$ in $\pi$, its y-coordinates must weakly agree with the ordering of $\tau$, i.e., $y_2 \le y_4 \le y_1 \le y_3$. As the points of $\pi$ correspond to the rotation of the $[n] \times [n]$ grid by a small positive angle, any pair of points on a horizontal line becomes an ascending pair, and any pair on a vertical line becomes a descending pair. Therefore, since $\tau (2) < \tau (3)$, we necessarily have $x_2 < x_3$ (they cannot lie on a vertical line), and since $\tau (1) > \tau (4)$ we necessarily have $y_1 > y_4$ (they cannot lie on a horizontal line). These two conditions imply that $|A|=4$, since any two points in A disagree on some coordinate. In fact, these conditions prevent all ascending pairs of $\tau$ from lying on a vertical line, and all descending pairs from lying on a horizontal line, and are therefore sufficient in order for A to induce a copy of $\tau$. Consequently,

$$\begin{aligned} {\# \mathtt { \tau } \left( \pi \right) }&= \Big | \big \{x_1 \le x_2< x_3 \le x_4,\ y_2 \le y_4< y_1 \le y_3\ :\ x_1,\dots ,x_4 \in [n],\ y_1,\dots ,y_4 \in [n] \big \} \Big | \\&= \Big | \big \{x_1 \le x_2< x_3 \le x_4\ :\ x_1,\dots ,x_4 \in [n] \big \} \times \big \{ y_2 \le y_4< y_1 \le y_3\ :\ y_1,\dots ,y_4 \in [n] \big \} \Big | \\&= \Big | \big \{x_1 \le x_2 < x_3 \le x_4\ :\ x_1,\dots ,x_4 \in [n] \big \} \Big |^2. \end{aligned}$$

In the latter case there are four possible choices to consider: a set of four distinct points; a triple with either ($x_1$ and $x_2$) or ($x_3$ and $x_4$) identified; or, a pair with both the aforementioned identifications. Therefore,

$$\begin{aligned} {\# \mathtt { \tau } \left( \pi \right) }&= \Big | \big \{x_1 \le x_2 < x_3 \le x_4\ :\ x_1,\dots ,x_4 \in [n] \big \} \Big |^2 \\&= \left( \left( {\begin{array}{c}n\\ 4\end{array}}\right) + 2\left( {\begin{array}{c}n\\ 3\end{array}}\right) + \left( {\begin{array}{c}n\\ 2\end{array}}\right) \right) ^2 = \left( {\begin{array}{c}n+2\\ 4\end{array}}\right) ^2. \end{aligned}$$

$\square$

Remark 5.5

Apart from $\tau = \texttt{3142}$, there is only one other pattern $\sigma = \texttt{2413}$ in $\mathbb {S}_4$, for which the distance is $\Theta (n^7)$. The computation for this pattern proceeds identically to the proof of Proposition 5.4, the only difference being the set of strict inequalities imposed. All remaining entries of the 4-profile of ${{\,\textrm{ES}\,}}^+(n)$ are indeed within $\mathcal {O}(n^6)$ of uniform.

5.2.1 A Modification of Erdős–Szekeres

We next define a modification of the Erdős–Szekeres permutation.

Definition 5.6

(two-sided Erdős–Szekeres). With n, m and $\varepsilon$ as in Definiton 5.3, the two-sided Erdős–Szekeres permutation, denoted ${{\,\textrm{ES}\,}}^\pm (n,m)$, is the permutation associated with the points $\mathcal {P}(\varepsilon ) \sqcup \mathcal {P}(-\varepsilon )$.⁴

The 4-profile of this family of permutations is optimally balanced, up to a multiplicative constant.

Theorem 8

(4-profile of two-sided Erdős–Szekeres). Let $n \ge 1$ and let $\pi = {{\,\textrm{ES}\,}}^{\pm }(n) \in \mathbb {S}_{2n^2}$ be the two-sided Erdős–Szekeres permutation. Then,

$$\begin{aligned} \delta _{\pi , 4} = \frac{2n^6}{9} + \mathcal {O}(n^5). \end{aligned}$$

Proof 9

Consider two copies of the $[n] \times [n]$ grid; one blue and one red. We slightly rotate the blue grid counterclockwise around the origin, so that any two points on a horizontal line become an ascending pair, and any two points on a vertical line become a descending pair. The red copy of the grid is likewise rotated clockwise, so that the above rules are reversed. These two rotations also enforce particular alignment (ascending or descending) to every bi-coloured pair of points on an axis-aligned line.

We turn to count the occurrences of any $\tau \in \mathbb {S}_4$ induced by the two grids. Let us first describe a counting process that applies to all patterns in $\mathbb {S}_4$ other than $\texttt{2413}$ and $\texttt{3142}$. In this process, our calculations are carried out on the integer grid, keeping in mind the rotations of the blue and red copies. So, consider some other pattern, say $\tau = \texttt{1243}$. Any instance of $\tau$ is determined by first fixing two ascending grid points and their colours, and naming them $(\texttt{ 2 })$ and $(\texttt{ 3 })$, respectively. It remains to fix $(\texttt{ 1 })$ and $(\texttt{ 4 })$. We observe that given a choice of the first two points, the feasible regions for either of the remaining points are defined by disjoint rectangles, whose corners are determined by the boundaries of the grid and by the coordinates of $(\texttt{ 2 })$ and $(\texttt{ 3 })$. Thus, for a fixed choice of the two points, the number of $\tau$-instances is simply the product of the volumes of both rectangles, where volume means the number of grid points (of either colour) within said rectangle.

Fig. 6

Counting the pattern $\tau = \texttt{1243}$ in ${{\,\textrm{ES}\,}}^\pm (n)$. Fixing the points $(\texttt{ 2 })$ and $(\texttt{ 3 })$ determines the feasible rectangles for $(\texttt{ 1 })$ and $(\texttt{ 4 })$. Coloured solid lines indicate that points of that colour may be taken at the boundary. Dashed lines indicate that they may not

Crucially, we remark that the colours of the two fixed points determine the “tie-breaks” in computing the volumes; for instance, if $(\texttt{ 2 })$ is a red point, then the bottom-left rectangle from which $(\texttt{ 1 })$ is sampled may include either colour on a vertical line with $(\texttt{ 2 })$, but cannot include red or blue points on a horizontal line with $(\texttt{ 2 })$. In more detail: say R and B are a red and a blue grid point, respectively, to the left of $(\texttt{ 2 })$. Then, the clockwise rotation of the red grid puts the rotated R higher than the rotated $(\texttt{ 2 })$, and the counterclockwise rotation of the blue grid puts the rotated B higher than the clockwise rotated $(\texttt{ 2 })$.

Consequently, for any $\tau \in \mathbb {S}_4 \setminus \left\{ \texttt{2413}, \texttt{3142} \right\}$, the number of occurrences of $\tau$ is characterised by a sum (over all two combinations of two fixed points) of the products of volumes of rectangles determined by these points. Rather than directly compute these sums, we take a shortcut: note that such an expression is a polynomial in n. Indeed, the volumes of the rectangles are clearly polynomials in the coordinates of their corners, and in n, and the sum is taken over all choices of the two fixed points. The remaining two patterns, $\texttt{2413}$ and $\texttt{3142}$ are inverses of one another, and by construction ${{\,\textrm{ES}\,}}^\pm (n)$ is an involution. Thus ${\# \mathtt { \sigma } \left( {{\,\textrm{ES}\,}}^\pm (n) \right) } = {\# \mathtt { \sigma ^{-1} } \left( {{\,\textrm{ES}\,}}^\pm (n) \right) }$ for any permutation $\sigma$, and in particular, ${\# \texttt{ 2413 } \left( {{\,\textrm{ES}\,}}^\pm (n) \right) } = {\# \texttt{ 3142 } \left( {{\,\textrm{ES}\,}}^\pm (n) \right) }$. Since the sum of all 4-profiles is $\left( {\begin{array}{c}n^2\\ 4\end{array}}\right)$, a polynomial in n, the remaining two pattern-counts are therefore also polynomials in n.

To conclude, every entry in the 4-profile of ${{\,\textrm{ES}\,}}^\pm (n)$ is a polynomial in n, of degree at most 8 (there are only $\Theta (n^8)$ four-tuples). The proof now follows by directly computing ${\# \mathtt { \tau } \left( {{\,\textrm{ES}\,}}^{\pm }(n) \right) }$ for all $n \in \{1, \dots , 9\}$, and for every $\tau \in \mathbb {S}_4$, and applying Lagrange interpolation over these points. $\square$

5.3 Profiles and Distance of Random Permutations

A simple probabilistic argument shows that for every fixed $k \ge 2$ and large n, the k-profile of almost every permutation in $\mathbb {S}_n$ is $\left( \left( {\begin{array}{c}n\\ k\end{array}}\right) /k! \pm o(n^k)\right) \mathbb {1}$. In this discussion we are interested in exactly how close to balanced the k-profile of a typical (random) permutation is, and in particular, whether this distance attains, or nearly attains, our lower bound in Theorem 7.

So fix some $k \ge 2$ and consider a pattern $\tau \in \mathbb {S}_k$. Associated with $\tau$ is the random variable $X_\tau {:}{=}{\# \mathtt { \tau } \left( \pi \right) }$ where $\pi$ is uniformly sampled from $\mathbb {S}_n$. Clearly, $\mathbb {E}[X_\tau ] = \left( {\begin{array}{c}n\\ k\end{array}}\right) /{k!}$. The distribution of $X_\tau$, its moments, and even the pairwise joint distributions of patterns have received considerable attention (e.g., [2, 9, 14, 15]). It is known in particular that $X_\tau$ satisfies a central limit theorem. Concretely, there exists a constant $\sigma _\tau > 0$ such that as $n \rightarrow \infty$,

This CLT implies asymptotic concentration and anti-concentration of k-profiles.

Proposition 5.7

(concentration and anti-concentration of k-profile). Let $k \ge 2$ be a constant and let $\sigma ^2 {:}{=}\max _{\tau \in \mathbb {S}_k} \sigma _\tau ^2$.⁵ Then, for any constant $\alpha > 0$ it holds that:

$$\begin{aligned} \Pr _{\pi \sim \mathbb {S}_n} \left[ \delta _{\pi , k} \ge \alpha \cdot n^{k-1/2} \right] \ge 2 \cdot \Phi \left( -\frac{\alpha }{\sigma k!}\right) \pm o(1),\ \ \ \ \ \ \end{aligned}$$

and conversely (by union over $\mathbb {S}_k$),

$$\begin{aligned} \Pr _{\pi \sim \mathbb {S}_n} \left[ \delta _{\pi , k} \le \alpha \cdot n^{k-1/2} \right] \ge 1 - 2 k! \cdot \Phi \left( -\frac{\alpha }{\sigma k!}\right) \pm o(1). \end{aligned}$$

In particular, this implies that $\delta _{\pi , k} \in \left( \frac{\sigma }{100 k!},\ \sigma (k+1)!\right) n^{k-1/2}$ with probability $> 99\%$ as $n \rightarrow \infty$.

6 An Asymptotic Relation Between Profiles and Permutations

So far we have considered k-profiles of order-n permutations with $k > 1$ fixed, and $n \rightarrow \infty$. But such profiles are interesting also when $k=k(n)$ grows with n. For example, as observed at the start of Sect. 4, when $k > rsim e \sqrt{n}$, at least some order-k permutations must be missing, i.e., the support of the k-profile is necessarily incomplete. Also, in the extreme case where $k=n$, the k-profile is a singleton. Our main discovery in this section is the following:

Profiles determine points. In the range $n\ge k(n) \ge \Omega (\sqrt{n} \log n)$, the k-profile of $\pi \in \mathbb {S}_n$ reveals a lot about $\pi$. Explicitly, we prove that there exists a set $\mathcal {D} \subset [n]^2$ of $\widetilde{\Omega }(k^4/n^2)$ points (consisting of four symmetric regions, of widths roughly $k^2/n$), such any two permutations in $\mathbb {S}_n$ with the same k-profile, must agree on their restriction to $\mathcal {D}$ (see Fig. 7). In the extreme case where $k=n$, our Theorem is close to tight, as the set $\mathcal {D}$ nearly covers the entire grid $[n] \times [n]$ (up to a logarithmic factor).

Fig. 7

The k-profile fully determines the restriction of any $\pi \in \mathbb {S}_n$ with that profile, to the red region

The main result of this section is Theorem 9. Its proof goes as follows: We define the evaluation $p(\pi )$ of a bivariate polynomial p over a permutation $\pi$. Then we show that if $\deg (p)<k$, then this real number $p(\pi )$ is uniquely defined by the k-profile of the permutation $\pi$. We subsequently use standard tools from approximation theory to construct a family of polynomials of degree $<k$, which allow us to uncover the points in $\mathcal {D}$.

6.1 k-Profiles Determine the Evaluation of Degree $< k$ Polynomials

Here is the main notion that we use in this section:

Notation 6.1

(evaluation of a polynomial on a permutation). Let $p \in \mathbb {R}[x,y]$ be a real bivariate polynomial and let $\pi \in \mathbb {S}_n$ be a permutation. The evaluation of p on $\pi$ is denoted:

$$\begin{aligned} p(\pi ) {:}{=}\sum _{i=1}^n p(i, \pi (i)). \end{aligned}$$

With this notation we show:

Proposition 6.2

(k-profile determines $(\deg < k)$-evaluations). Let $p \in \mathbb {R}[x,y]$ be a bivariate polynomial with $\deg (p) < k$ for some integer $k > 1$. Also, let $\pi \in \mathbb {S}_n$ be a permutation of order $n\ge k$. Then $p(\pi )$ is uniquely determined by the k-profile of $\pi$.

Proof 10

For any two integers $1 \le t< r < k$, consider the following event, in which all indices are sampled uniformly at random and independently from $\{1, \dots , n\}$:

$$\begin{aligned}&\Pr _{\begin{array}{c} x_1, \dots , x_t\\ y_1, \dots , y_{r-t} \\ i \end{array}} \hspace{-0.2cm}\big [ x_1, \dots , x_t \le i,y_1, \dots , y_{r-t} \le \pi (i) \big ] \\&\quad = \sum _{z=1}^n \Pr _{\begin{array}{c} x_1, \dots , x_t \\ y_1, \dots , y_{r-t} \end{array}} \hspace{-0.1cm}\big [ x_1, \dots , x_t \le z, y_1, \dots , y_{r-t} \le \pi (z) \big ] \Pr _{i} [i=z] \\&\quad = \frac{1}{n} \sum _{z=1}^n \Pr _{x_1, \dots , x_t} \big [ x_1, \dots , x_t \le z] \Pr _{y_1, \dots , y_{r-t}} \big [ y_1, \dots , y_{r-t} \le \pi (z) \big ] \\&\quad = \frac{1}{n} \sum _{z=1}^n \left( \frac{z}{n}\right) ^t \cdot \left( \frac{\pi (z)}{n}\right) ^{r-t} = \frac{1}{n^{r+1}} (x^t y^{r-t})(\pi ), \end{aligned}$$

where the first equality follows from the law of total probability, and the latter ones by independence. Conversely, by conditioning on the possible equalities between the sampled indices, the same event can be expressed as a weighted sum of permutation patterns over $(\le k)$-points (see proof of Lemma 4.3). By Proposition 2.4, fixing the k-profile determines all r-profiles, where $r < k$. This proves the proposition for $p(x,y)=x^t y^{r-t}$, and the proof now follows, since these monomials span all bivariate polynomials of degree $<k$.⁶$\square$

Remark 6.3

Proposition 6.2 can be extended by analysing a different set of events. For example, for any $r < k$ and $\tau \in \mathbb {S}_r$, we could consider the event in which we sample r permutation points, and condition on their relative ordering so that they form an instance of $\tau$ in $\pi$. Then, using the remaining budget of at most $k-r$ points, we could sample from their marginals. Such events determine the evaluations of many more polynomials (albeit, on a modified and weighted pointset).

6.2 Determining Points Using Approximate Indicators

Here is our method for “reading the bit” at position (x, y). We construct to this end a low-degree polynomial that is a good pointwise approximator of the indicator $\mathbb {1}_{(x,y)}: [n]^2 \rightarrow \{0,1\}$. If the polynomial has degree $<k$ and the approximation error is small, then by evaluating it, we can determine the value of the corresponding bit. This means that either every permutation $\pi$ with a given k-profile must contain this point, or none of them do, and the evaluation of the polynomial will reveal this.

For notational convenience, in what follows we consider (as in Sect. 3) the action $\langle r \rangle \curvearrowright [1,n]^2$ of the $90^\circ$-rotation. We denote by $O(a,b) = \{ (a,b), (b, n+1-a), (n+1-a, n+1-b), (n+1-b, a)\}$ the r-orbit of $(a,b) \in [n]^2$. Similarly, for a set $\mathcal {D} \subset [n]^2$ we denote $O(\mathcal {D}) {:}{=}\cup _{(a,b) \in \mathcal {D}} O(a,b)$ (i.e., the r-orbit of $\mathcal {D}$). The following fact is well-known and easy to verify (e.g., [20]).

Lemma 6.4

(symmetrisation). Let $p : \{0,1\}^n \rightarrow \mathbb {R}$ be a real multilinear polynomial, and let $f: \{0, 1, \dots , n\} \rightarrow \mathbb {R}$ be the function given by

$$\begin{aligned} f(k) = \mathbb {E}_{|x| \sim k}[p(x)] \quad \quad \forall k \in \{0,1, \dots n\}, \end{aligned}$$

where the expectation is taken with respect to the uniform distribution over all $x \in \{0,1\}^n$ of Hamming weight k. Then, f can be written as a real polynomial in k of degree at most $\deg (p)$.

Lemma 6.5

(approximate degree of symmetric boolean functions⁷ [23]). Let $f: \{0,1\}^n \rightarrow \{0,1\}$ be a symmetric Boolean function, and let:

$$\begin{aligned} \Gamma (f) = \min _k \{ |2k - n + 1| : f_{k} \ne f_{k+1} \}, \end{aligned}$$

where $f_k$ is the value of f on inputs of Hamming weight k. Then, there exists a multilinear polynomial $g \in \mathbb {R}[x_1, \dots , x_n]$ such that $\forall x \in \{0,1\}^n: |g(x) - f(x)| \le 1/3$, and furthermore:

$$\begin{aligned} \deg (g) \le A \cdot \sqrt{n \left( n - \Gamma (f) \right) }, \end{aligned}$$

where $A > 0$ is a universal constant.

Lemma 6.6

(one-sided approximation of $\mathbb {1}_{(a,b)}$). Let u, v and n be integers such that $1 \le u,v < n/2$. Then, for any $(a,b) \in O(u,v)$, there exists a polynomial $\widetilde{\mathbb {1}}_{(a,b)} \in \mathbb {R}[x,y]$ such that:

$$\begin{aligned} \deg \left( \widetilde{\mathbb {1}}_{(a,b)}\right) \le C \left( \sqrt{n(2u+1)} + \sqrt{n(2v+1)}\right) \log n, \end{aligned}$$

where $C > 0$ is an absolute constant, and:

$$\begin{aligned} \forall (x,y) \in [n]^2:\ \widetilde{\mathbb {1}}_{(a,b)}(x,y) \in {\left\{ \begin{array}{ll} {[}1, \infty ) & x=a \wedge y=b; \\ {[}0, \frac{1}{2n}] & x \ne a \vee y \ne b. \end{array}\right. } \end{aligned}$$

Proof 11

For any $t \in [n]$, let $H_t: \{0,1\}^n \rightarrow \{0,1\}$ be the symmetric Boolean function $H_t(x) {:}{=}\mathbb {1}\{ |x| = t \}$, where |x| is the Hamming weight of $x \in \{0,1\}^n$. By construction, $\Gamma (H_t) \in |2t - n \pm 1|$. An application of Lemma 6.5 to $H_t$ gives a real multilinear polynomial $G_t \in \mathbb {R}[x_1, \dots , x_n]$ such that $\forall x \in \{0,1\}^n: | H_t(x) - G_t(x) | \le 1/3$, and whose degree is bounded by $A (n(n - \Gamma (H_t))^{1/2}$ where $A > 0$ is an absolute constant (independent of n, t). Consider $f_t: \{0, 1, \dots , n\} \rightarrow \mathbb {R}$, the symmetrisation of $G_t$. By Lemma 6.4, $f_t$ is a univariate polynomial of degree at most $\deg (G_t)$. Since $H_t$ is constant over all inputs of the same Hamming weight, and $G_t$ approximates $H_t$ pointwise to error at most 1/3, we have that $\big | f_t(x) - \mathbb {1}_t (x) \big | \le \frac{1}{3}$ for every $x \in [n]$, and therefore,

$$\begin{aligned} \left( f_t(x) + \frac{1}{3}\right) \in {\left\{ \begin{array}{ll} {[}1, \frac{5}{3}] & x = t; \\ {[}0, \frac{2}{3}] & x \ne t. \end{array}\right. } \end{aligned}$$

To conclude the proof, let $(a,b) \in O(u,v)$ where $u,v < n/2$, and consider the following polynomial:

$$\begin{aligned} \widetilde{\mathbb {1}}_{(a,b)}(x,y) = \left[ \left( f_a(x) + \frac{1}{3}\right) \left( f_b(y) + \frac{1}{3}\right) \right] ^{ \lceil \log _{{3}/{2}}2n \rceil } \in \mathbb {R}[x,y]. \end{aligned}$$

Taking the products and powers of the aforementioned bounds on $f_t$, it follows that:

$$\begin{aligned} \forall (x,y) \in [n]^2:\ \widetilde{\mathbb {1}}_{(a,b)}(x,y) \in {\left\{ \begin{array}{ll} {[}1, \infty ) & x=a \wedge y=b; \\ {[}0, (\frac{2}{3})^{\lceil \log _{{3}/{2}}2n \rceil }] & x \ne a \vee y \ne b. \end{array}\right. } \end{aligned}$$

Lastly, by construction, the total degree of $\widetilde{\mathbb {1}}_{(a,b)}$ is bounded by $A (\sqrt{n(2u+1)} + \sqrt{n(2v+1)}) \lceil \log _{{3}/{2}} (2n)\rceil$, and the proof now follows for an appropriate choice of C. $\square$

Theorem 9

(k-profiles determine points). Let $n \ge k > 1$ and let:

$$\begin{aligned} \mathcal {D} = \Big \{ (a,b) \in \left[ n/2 \right] ^2\ :\ C \left( \sqrt{n(2a+1)} + \sqrt{n(2b+1)}\right) \log n < k \Big \} \subset [n]^2, \end{aligned}$$

where C is the constant of Lemma 6.6. Then the k-profile of an order-n permutation $\pi \in \mathbb {S}_n$ uniquely determines the restriction of $\pi$ to $O(\mathcal {D})$.

Proof 12

Let $(a,b) \in O(\mathcal {D})$ and let $\widetilde{\mathbb {1}}_{(a,b)}$ be the one-sided approximation given by Lemma 6.6. By construction, for every permutation $\pi \in \mathbb {S}_n$ we have $\widetilde{\mathbb {1}}_{(a,b)}(\pi ) \ge 1$ iff $(a,b) \in \{(i, \pi (i)) : i \in [n]\}$, and $\widetilde{\mathbb {1}}_{(a,b)}(\pi ) \le (1/2n) \cdot n \le 1/2$ otherwise. So, this evaluation determines the presence or absence of (a, b). From Lemma 6.6, it follows that $\deg (\widetilde{\mathbb {1}}_{(a,b)}) < k$, and thus (by Proposition 6.2), all permutations with a given k-profile must agree on this polynomial, and on the coordinate (a, b). $\square$

7 Discussion

In this paper we consider the existence of k-balanced permutations. For $k \le 3$ we show that such permutations exist whenever n satisfies the necessary divisibility conditions, and for $k \ge 4$, we show that no such permutations exist. Moreover, we prove that the k-profile of any n-element permutation must have an entry which is $\Omega _n(n^{k-1})$ away from uniform, whenever $k \ge 4$. This gives rise to several interesting open questions.

Is the lower bound tight? Recall that for $k=4$ we provide an explicit construction of an infinite family (see Sect. 5.2.1) in which every pattern in $\mathbb {S}_4$ appears within additive distance of $\Theta (n^{3})$ from uniform, i.e., matching the lower bound of Theorem 7. Conversely, we note (see Sect. 5.3) that all entries in the k-profile of a uniformly random permutation in $\mathbb {S}_n$ are, with probability $>99\%$ (for large enough n), within distance $\Theta (n^{k - 1/2})$ from uniform. In this view we ask what is the true behaviour for $k>4$. Specifically, does our lower bound remain tight, or does the true bound change to $\Omega (n^{k-1/2})$, as attained by the majority of permutations?

How many k-patterns can appear the right number of times? We have ruled out the possibility that every entry in the 4-profile equals $\left( {\begin{array}{c}n\\ 4\end{array}}\right) /4!$. However, for any fixed pattern $\tau \in \mathbb {S}_4$, we are able to construct a bespoke infinite family of permutations, in whose members $\tau$ appears exactly $\left( {\begin{array}{c}n\\ 4\end{array}}\right) /4!$ times (these constructions are quite intricate, and are not included in this paper). So, we ask: how many entries in the k-profile of an n-element permutation may be precisely $\left( {\begin{array}{c}n\\ k\end{array}}\right) /k!$, simultaneously?

What is the maximal dimension of a k-balanced subspace? It makes sense to ask the same question with regards to linear subspaces. That is, what is the maximal dimension of a subspace $V_k \le \mathbb {R}^{\mathbb {S}_k}$ such that there exist infinitely many permutations $\pi \in \mathbb {S}_n$ for which:

$$\begin{aligned} \forall v = (\alpha _{\tau })_{\tau \in \mathbb {S}_k} \in V_k:\ \frac{\left( {\begin{array}{c}n\\ k\end{array}}\right) }{k!} \langle v, \mathbb {1}_{\mathbb {S}_k} \rangle = \sum _{\tau \in \mathbb {S}_k} \alpha _\tau {\# \mathtt { \tau } \left( \pi \right) }. \end{aligned}$$

In other words, unlike the previous question, here we allow any basis for $V_k$, not necessarily only the coordinate vectors. Clearly $\langle \mathbb {1}_{\mathbb {S}_k} \rangle \in V_k$, for any k. Also, since 3-balanced permutations exist, then by Proposition 2.4 there are $3!=6$ linearly independent combinations in $\mathbb {S}_4$ that hold true, and $\dim (V_4) \ge 6$ ($\mathbb {1}_{\mathbb {S}_k}$ resides in their span). In general, we ask: what is the maximal dimension of $V_k$, for $k \ge 4$?

How many permutations are 3-balanced? 2- and 3-balanced permutations exist for every admissible value of n (see Sect. 3). In fact, they never appear “alone”: as they are closed under the action of $D_4$, their entire orbit is also balanced and so there must at least be two balanced permutations, whenever one exists (no permutation is identical to its reflection about either axis). Therefore, we ask: what is the exact count, or even asymptotic growth rate, of 3-balanced permutations (restricted only to the admissible n)? We remark that for 2-balanced permutations these answers are already known (see [22, A316775] and [22, A000140]). However, interestingly, for $k=3$ we presently only know that at $n=9$ there are exactly two $3$-balanced permutations (see Fig. 2).

Appendices

3-Balanced Constructions for All Remainders

In the proof of Theorem 5 we amended $\sigma$ by inserting two points, yielding $3$-balanced permutations for every $n > 56$ with $n \equiv 20 \pmod {36}$. The same strategy applies to the other residues as well, as we now describe. In the following discussion $\ell = 3t+1$, and $0< \varepsilon < 1$ is a small constant.

To prove the correctness of these constructions, we observe that all newly inserted coordinates are affine transformations of t. Consequently, each 2-pattern (resp. 3-pattern) count in $\sigma$ is a quadratic (resp. cubic) polynomial in t. It follows that Equaiton (2) posits the vanishing of a cubic polynomial. This we can verify by checking only four distinct values of t. This is an alternative to the calculation presented in Theorem 5.

1.1 Constructions for Even n

In Theorem 5, we amended $\sigma \in \mathbb {S}_m$ by inserting two additional points:

and showed that for any $t\ge 2$, one can set $r=4t+2$ to satisfy Equaiton (2). The size of the resulting $3$-balanced permutation $\pi \in \mathbb {S}_n$ obtained by rotation is $n=4m=36t+20$, that is, $n \equiv 20 \pmod {36}$.

The case $n \equiv 28 \pmod {36}$. Insert two more points to $\sigma$, so that $m=3\ell +4$:

The case $n \equiv 0 \pmod {36}$. Insert two more points, in addition to the above four:

1.2 Constructions for Odd n

For $t \ge 4$, inserting the following points (and a point at the centre of $\pi$) yields $3$-balanced permutations.

The case $n \equiv 29 \pmod {36}$. Insert four points to $\sigma$, so that $m=3\ell +4$:

The case $n \equiv 1 \pmod {36}$. Insert two more points to $\sigma$, so that now $m=3\ell +6$:

The case $n \equiv 9 \pmod {36}$. Insert two last points to $\sigma$, in addition to the previous six. So, $m=3\ell +8$:

1.3 Small Cases Not Covered by Our Construction

For completeness, we provide a list of 3-balanced permutations in Table 1, for these values of n that were not covered by the aforementioned constructions. This is because Theorem 5, Sect. A.1 and Sect. A.2 yield $3$-balanced permutations for every residue modulo 36, starting only from some minimal value of t.

Table 1 3-balanced permutations for all values of n not covered by our constructions

Computation of Lemma 4.3

In the proof of Lemma 4.3 we fix $\pi \in \mathbb {S}_n$ and consider the event:

$$\begin{aligned} \Pr _{i,j,k,l \sim [n]} \left[ i< j,\ \pi (i)< \pi (j),\ k< l,\ \pi (k) < \pi (l) \right] . \end{aligned}$$

The proof of Lemma 4.3 proceeds by showing that, by conditioning on the possible equalities between the sampled indices and on their total order, the aforementioned event can be expressed as a polynomial involving pattern-counts in $\pi$, of lengths at most 4. The complete details of this computation are presented in Table 2. The first column of the table corresponds to the partition over the indices, where two indices are identical if and only if they reside in the same set. The second column corresponds to a fixed linear order over the indices at play, and the third column lists the contributing patterns, conditioned over the first two events. The total probability is then computed by summing over the probabilities of each row. Every row containing a partition of cardinality r, a linear order, and a set of patterns $S \subset \mathbb {S}_r$, indicates an event occurring with probability:

$$\begin{aligned} \frac{\prod _{i=1}^r (n-i+1) }{n^4} \cdot \frac{1}{r!} \cdot \sum _{\tau \in S} \frac{{\# \mathtt { \tau } \left( \pi \right) }}{\left( {\begin{array}{c}n\\ r\end{array}}\right) }. \end{aligned}$$

Table 2 The terms corresponding to the computation of the total probability of the event analysed in the proof of Lemma 4.3. The partitions and orderings which do not contribute are omitted