Skip to main content
SpringerLink
Log in

Sequential decision aggregation with social pressure

  • Original Article
  • Published:
Mathematics of Control, Signals, and Systems Aims and scope Submit manuscript

Abstract

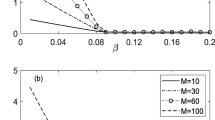
This paper proposes and characterizes a sequential decision aggregation system consisting of agents performing binary sequential hypothesis testing and a fusion center which collects the individual decisions and reaches the global decision according to some threshold rule. Individual decision makers’ behaviors in the system are influenced by other decision makers, through a model for social pressure; our notion of social pressure is proportional to the ratio of individual decision makers who have already made the decisions. For our proposed model, we obtain the following results: First, we derive a recursive expression for the probabilities of making the correct and wrong global decisions as a function of time, system size, and the global decision threshold. The expression is based on the individual decision makers’ decision probabilities and does not rely on the specific individual decision-making policy. Second, we discuss two specific threshold rules: the fastest rule and the majority rule. By means of a mean-field analysis, we relate the asymptotic performance of the fusion center, as the system size tends to infinity, to the individual decision makers’ decision probability sequence. In addition to theoretical analysis, simulation work is conducted to discuss the speed/accuracy tradeoffs for different threshold rules.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6

Similar content being viewed by others

References

  1. Wald A (1945) Sequential tests of statistical hypotheses. Ann Math Stat 16(2):117–186

    Article  MathSciNet  MATH  Google Scholar 

  2. Shiryaev AN (1961) On optimum methods in quickest detection problems. Theory Probab Appl 8(1):22–46

    Article  MATH  Google Scholar 

  3. Woudenberg F (1991) An evaluation of Delphi. Technol Forecast Soc Change 40(2):131–150

    Article  Google Scholar 

  4. Tsitsiklis JN (1993) Decentralized detection. Adv Stat Signal Process 2:297–344

    Google Scholar 

  5. Irving WW, Tsitsiklis JN (1994) Some properties of optimal thresholds in decentralized detection. IEEE Trans Autom Control 39(4):835–838

    Article  MathSciNet  MATH  Google Scholar 

  6. Veeravalli VV, Başar T, Poor HV (1994) Decentralized sequential detection with sensors performing sequential tests. Math Control Signals Syst 7(4):292–305

    Article  MathSciNet  MATH  Google Scholar 

  7. Varshney PK (1997) Distributed detection and data fusion. Springer, New York

    Book  Google Scholar 

  8. Veeravalli VV (2001) Decentralized quickest change detection. IEEE Trans Inf Theory 47(4):1657–1665

    Article  MathSciNet  MATH  Google Scholar 

  9. Goldenberg J, Libai B, Muller E (2001) Talk of the network: a complex systems look at the underlying process of word-of-mouth. Mark Lett 12:211–223

    Article  Google Scholar 

  10. Chamberland JF, Veeravalli VV (2003) Decentralized detection in sensor networks. IEEE Trans Signal Process 51:407–416

    Article  Google Scholar 

  11. Gale D, Kariv S (2003) Bayesian learning in social networks. Games Econ Behav 45(2):329–346

    Article  MathSciNet  MATH  Google Scholar 

  12. Kerr NL (2004) Group performance and decision making. Ann Rev Psychol 55:623–655

    Article  Google Scholar 

  13. Gardner M, Steinberg L (2005) Peer influence on risk taking, risk preference, and risky decision making in adolescence and adulthood: an experimental study. Dev Psychol 41(4):625–635

    Article  Google Scholar 

  14. Bharathi S, Kempe D, Salek M (2007) Competitive influence maximization in social networks. Internet Netw Econ 4858:306–311

    Article  Google Scholar 

  15. Carnes T, Nagarajan C, Wild SM, van Zuylen A (2007) Maximizing influence in a competitive social network: a follower’s perspective. In: International conference on electronic commerce. Minneapolis, USA, pp 351–360

  16. Le Boudec JY, McDonald D, Mundinger J (2007) A generic mean field convergence result for systems of interacting objects. In: International conference on quantitative evaluation of systems. Edinburgh, Scotland, pp 3–18

  17. Epstein LG, Noor J, Sandroni A (2008) Non-bayesian updating: a theoretical framework. Theor Econ 3(2):193–229

    Google Scholar 

  18. Acemoglu D, Dahleh MA, Lobel I, Ozdaglar A (2011) Bayesian learning in social networks. Rev Econ Stud 78(4):1201–1236

    Article  MathSciNet  MATH  Google Scholar 

  19. Acemoglu D, Ozdaglar A (2011) Opinion dynamics and learning in social networks. Dyn Games Appl 1(1):3–49

    Article  MathSciNet  MATH  Google Scholar 

  20. Lorenz J, Rauhut H, Schweitzer F, Helbing D (2011) How social influence can undermine the wisdom of crowd effect. Proc Natl Acad Sci 108(22):9020–9025

    Article  Google Scholar 

  21. Dandach SH, Carli R, Bullo F (2012) Accuracy and decision time for sequential decision aggregation. Proc IEEE 100(3):687–712

    Article  Google Scholar 

  22. Kimura M, Moehlis J (2012) Group decision-making models for sequential tasks. SIAM Rev 54:121–138

    Article  MathSciNet  MATH  Google Scholar 

  23. Jadbabaie A, Molavia P, Sandroni A, Tahbaz-Salehi A (2012) Non-bayesian social learning. Games Econ Behav 76(1):210–225

    Article  MathSciNet  MATH  Google Scholar 

  24. Shirazipourazad S, Bogard B, Vachhani H, Sen A, Horn P (2012) Influence propagation in adversarial setting: how to defeat competition with least amount of investment. In: ACM international conference on information and knowledge management. Maui, USA, pp 585–594

  25. Baddeley M, Parkinson S (2012) Group decision-making: an economic analysis of social influence and individual difference in experimental juries. J Soc Econ 41(5):558–573

    Article  Google Scholar 

  26. Srivastava V, Leonard NE (2014) Collective decision-making in ideal networks: the speed-accuracy trade-off. IEEE Trans Control Netw Syst 1(1):121–132

    Article  MathSciNet  Google Scholar 

  27. Goyal S, Heidari H, Kerans M (2014) Competitive contagion in networks. Games Econ Behav (in press)

  28. Tinson JS, Nuttall PJ (2014) Social collective decision making among adolescents: a review and a revamp. Psychol Mark 31(10):871–885

    Article  Google Scholar 

  29. Kempe D, Kleinberg J, Tardos E (2015) Maximizing the spread of influence through a social network. Theory Comput 11(4):105–147

    Article  MathSciNet  MATH  Google Scholar 

  30. Poulakakis I, Young GF, Scardovi L, Leonard NE (2015) Information centrality and ordering of nodes for accuracy in noisy decision-making networks. IEEE Trans Autom Control 61(4):1040–1045

    Article  MathSciNet  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Department of Mechanical Engineering, University of California, Santa Barbara, USA

    Wenjun Mei & Francesco Bullo

Authors
  1. Wenjun Mei
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Francesco Bullo
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Wenjun Mei.

Additional information

This work was supported by the Institute for Collaborative Biotechnologies through Grant W911NF-09-D-0001 from the U.S. Army Research Office and through Grant W911NF-15-1-0274 from the U.S. Army Research Office. The content of the information does not necessarily reflect the position or the policy of the Government, and no official endorsement should be inferred.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Mei, W., Bullo, F. Sequential decision aggregation with social pressure. Math. Control Signals Syst. 28, 23 (2016). https://doi.org/10.1007/s00498-016-0174-5

Download citation

  • Received:

  • Accepted:

  • Published:

  • DOI: https://doi.org/10.1007/s00498-016-0174-5

Keywords

Search

Navigation