Skip to main content
Springer Nature Link
Log in

A sampled-data approach to optimal relaxed-causal sampling

  • Original Article
  • Published:
Mathematics of Control, Signals, and Systems Aims and scope Submit manuscript

Abstract

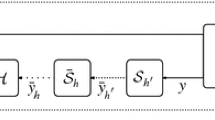
This paper studies the design of an optimal relaxed causal sampler using sampled data system theory. A lifted frequency domain approach is used to obtain the existence conditions and optimal sampler. A state-space formulation of the results is also provided. The resulting optimal relaxed causal sampler is a cascade of a linear continuous-time system followed by a generalized sampler and a discrete system.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4

Similar content being viewed by others

Notes

  1. This condition is with the constraint that \(\breve{G}_{{\text{ v }}}\) is causal.

References

  1. Bamieh BA, Pearson JB (1992) A general framework for linear periodic systems with applications to \({H}^\infty \) sampled-data control. IEEE Trans Autom Control 37:418–435

    Article  MathSciNet  Google Scholar 

  2. Bamieh BA, Pearson JB (1992) The \({H}^2\) problem for sampled-data systems. Syst Control Lett 19:1–12

    Article  Google Scholar 

  3. Boche H, Pohl V (2007) There is no free lunch with causal approximations. In: IEEE international conference on acoustics, speech and signal processing

  4. Chen T, Francis BA (1995) Design of multirate filter banks by \(H^\infty \) optimization. IEEE Trans Signal Process 43(12):2822–2830

    Article  Google Scholar 

  5. Chen T, Francis BA (1995) Optimal sampled-data control systems. Springer, New York

    Book  Google Scholar 

  6. Gohberg I, Kaashoek MA (1984) Time varying linear systems with boundary conditions and integral operators. I. The transfer operator and its properties. Integr Eqn Oper Theory 7:325–391

    Article  MathSciNet  Google Scholar 

  7. Gu G (2012) Discrete-time linear systems: theory and design with applications. Springer, New York

    Book  Google Scholar 

  8. Ishii H, Yamamoto Y, Francis BA (1999) Sample-rate conversion via sampled-data \(H^\infty \) control. IEEE Conf Decis Control 4:3440–3445

    Google Scholar 

  9. Kakemizu H, Nagahara M, Kobayashi A, Yamamoto Y (2005) Noise reduction of jpeg images by sampled-data \(H^\infty \) optimal \(\epsilon \) filters. In: SICE annual conference

  10. Khargonekar PP, Poolla KR, Tannenbaum A (1985) Robust control of linear time-invariant plants using periodic control. IEEE Trans Autom Control 30:1088–1096

    Article  Google Scholar 

  11. Khargonekar PP, Sivashankar N (1991) \(H_2\) optimal control for sampled-data systems. Syst Control Lett 17(6):425–436

    Article  Google Scholar 

  12. Khargonekar PP, Yamamoto Y (1996) Delayed signal reconstruction using sampled-data control. IEEE Conf Decis Control 2:1259–1263

    Article  Google Scholar 

  13. Konstantinov MM (2003) Perturbation theory for matrix equations. Elsevier, Amsterdam

    MATH  Google Scholar 

  14. Krener AJ (1980) Boundary value linear systems. Asterisque 75:149–165

    MathSciNet  MATH  Google Scholar 

  15. Kristalny M (2010) Exploiting previewed information in estimation and control. PhD thesis, Technion, Haifa, Israel

  16. Loan CV (1978) Computing integrals involving the matrix exponential. IEEE Trans Autom Control 23(3):395–404

    Article  MathSciNet  Google Scholar 

  17. Meinsma G, Mirkin L (2009) Sampling from a system-theoretic viewpoint. Memorandum, Department of Applied Mathematics, University of Twente. http://eprints.eemcs.utwente.nl/16463/

  18. Meinsma G, Mirkin L (2010) Sampling from a system-theoretic viewpoint: part I|concepts and tools. IEEE Trans Signal Process 58(7):3578–3590

    Article  MathSciNet  Google Scholar 

  19. Meinsma G, Mirkin L (2010) Sampling from a system-theoretic viewpoint: part II|non-causal solutions. IEEE Trans Signal Process 58(7):3591–3606

    Article  MathSciNet  Google Scholar 

  20. Meinsma G, Mirkin L (2012) \(L^2\) sampled signal reconstruction with causality constraints—part I: setup and solutions. IEEE Trans Signal Process 60(5):2260–2272

    Article  MathSciNet  Google Scholar 

  21. Meinsma G, Mirkin L (2012) \(L^2\) sampled signal reconstruction with causality constraints—part II: theory. IEEE Trans Signal Process 60(5):2273–2285

    Article  MathSciNet  Google Scholar 

  22. Mirkin L (2005) Transfer functions of sampled-data systems in the lifted domain. In: Proceeding 44th IEEE conference on decision and control and ECC’05, pp 5180–5185

  23. Mirkin L, Palmor ZJ (1999) A new representation of the parameters of lifted systems. IEEE Trans Autom Control 44(4):833–840

    Article  MathSciNet  Google Scholar 

  24. Mirkin L, Rotstein H, Palmor ZJ (1999) \(H^2\) and \(H^\infty \) design of sampled-data systems using lifting. Part I: general framework and solutions. SIAM J Control Optim 38(1):175–196

    Article  MathSciNet  Google Scholar 

  25. Mirkin L, Rotstein H, Palmor ZJ (1999) \(H^2\) and \(H^\infty \) design of sampled-data systems using lifting. Part II: properties of systems in the lifted domain. SIAM J Control Optim 38(1):197–218

    Article  MathSciNet  Google Scholar 

  26. Mirkin L, Tadmor G (2007) On geometric and analytic constraints in the \(H^\infty \) fixed-lag smoothing. IEEE Trans Autom Control 52(8):1514–1519

    Article  MathSciNet  Google Scholar 

  27. Mirkin L, Zaslavsky R (2005) A frequency-domain solution to the sampled-data \(H^2\) smoothing problem. In: IEEE conference on decision and control, pp 5186–5191

  28. Nagahara M (2003) Multirate digital signal processing via sampled-data H-infinity optimization. PhD thesis, Kyoto University, Kyoto, Japan

  29. Nagahara M, Yamamoto Y (2000) A new design for sample-rate converters. IEEE Conf Decis Control 5:4296–4301

    Google Scholar 

  30. Pohl V, Boche H (2009) Advanced topics in system and signal theory: a mathematical approach. Springer, New York

    MATH  Google Scholar 

  31. Shekhawat HS (2012) Optimal sampling and interpolation. PhD thesis, University of Twente, Enschede, The Netherlands. https://doi.org/10.3990/1.9789036534734

  32. Shekhawat HS, Meinsma G (2014) Optimal relaxed causal sampling from system theoretic viewpoint. Memorandum, Department of Applied Mathematics, University of Twente. http://doc.utwente.nl/91927/

  33. Shekhawat HS, Meinsma G (2015) A sampled-data approach to optimal non-causal downsampling. Math Control Signals Syst 27(3):277–315

    Article  MathSciNet  Google Scholar 

  34. Sun W, Nagpal KM, Khargonekar PP (1991) \(H_\infty \) control and filtering with sampled measurements. In: American control conference, pp 1652–1657

  35. Sun W, Nagpal KM, Khargonekar PP (1993) \(H_\infty \) control and filtering for sampled-data systems. IEEE Trans Autom Control 38(8):1162–1175

    Article  Google Scholar 

  36. Sun W, Nagpal KM, Khargonekar PP (1993) Optimal sampler for \(H_\infty \) control. In: IEEE conference on decision and control, pp 777–782

  37. Yamamoto K, Nagahara M, Yamamoto Y (2017) Signal reconstruction with generalized sampling. In: IEEE conference on decision and control, pp 6253–6258

  38. Yamamoto Y (1990) New approach to sampled-data control systems—a function space method. IEEE Conf Decis Control 3:1882–1887

    Article  Google Scholar 

  39. Yamamoto Y (1994) A function space approach to sampled-data control systems and tracking problems. IEEE Trans Autom Control 39:703–712

    Article  MathSciNet  Google Scholar 

  40. Yamamoto Y, Nagahara M, Khargonekar PP (2012) A brief overview of signal reconstruction via sampled-data \(H^\infty \) optimization. Appl Comput Math 11(1):3–18

    MathSciNet  MATH  Google Scholar 

  41. Yamamoto Y, Nagahara M, Khargonekar PP (2012) Signal reconstruction via \(H^\infty \) sampled-data control theory—beyond the Shannon paradigm. IEEE Trans Signal Process 60(2):613–625

    Article  MathSciNet  Google Scholar 

  42. Yamamoto Y, Yamamoto K, Nagahara M (2018) Sampled-data filters with compactly supported acquisition prefilters. In: IEEE conference on decision and control, pp 6650–6655

  43. Young N (1988) An introduction to Hilbert space. Cambridge University Press, Cambridge

    Book  Google Scholar 

  44. Zhou K, Doyle JC, Glover K (1996) Robust and optimal control. Prentice Hall, Upper Saddle River

    MATH  Google Scholar 

Download references

Acknowledgements

We are thankful to Prof. Leonid Mirkin and Dr. Maxim Kristalny (Technion, Israel) for many helpful discussions and suggestions.

Author information

Author notes

  1. Hanumant Singh Shekhawat

    Present address: Indian Institute of Technology Guwahati, Guwahati, India

Authors and Affiliations

  1. University of Twente, Enschede, The Netherlands

    Hanumant Singh Shekhawat & Gjerrit Meinsma

Authors
  1. Hanumant Singh Shekhawat
    View author publications

    You can also search for this author inPubMed Google Scholar

  2. Gjerrit Meinsma
    View author publications

    You can also search for this author inPubMed Google Scholar

Corresponding author

Correspondence to Hanumant Singh Shekhawat.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

The material in this paper was partially presented at the 20th International Symposium on Mathematical Theory of Networks and Systems (MTNS), July 9–13, 2012, Melbourne, Australia, with the title optimal relaxed causal sampler using sampled-data system theory.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Shekhawat, H.S., Meinsma, G. A sampled-data approach to optimal relaxed-causal sampling. Math. Control Signals Syst. 33, 669–705 (2021). https://doi.org/10.1007/s00498-021-00297-9

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00498-021-00297-9

Keywords