Skip to main content
SpringerLink
Log in

Benchmarking and comparison of nature-inspired population-based continuous optimisation algorithms

  • Methodologies and Application
  • Published:
Soft Computing Aims and scope Submit manuscript

Abstract

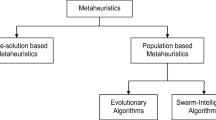
This paper describes an experimental investigation into four nature-inspired population-based continuous optimisation methods: the Bees Algorithm, Evolutionary Algorithms, Particle Swarm Optimisation, and the Artificial Bee Colony algorithm. The aim of the proposed study is to understand and compare the specific capabilities of each optimisation algorithm. For each algorithm, thirty-two configurations covering different combinations of operators and learning parameters were examined. In order to evaluate the optimisation procedures, twenty-five function minimisation benchmarks were designed by the authors. The proposed set of benchmarks includes many diverse fitness landscapes, and constitutes a contribution to the systematic study of optimisation techniques and operators. The experimental results highlight the strengths and weaknesses of the algorithms and configurations tested. The existence and extent of origin and alignment search biases related to the use of different recombination operators are highlighted. The analysis of the results reveals interesting regularities that help to identify some of the crucial issues in the choice and configuration of the search algorithms.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8

Similar content being viewed by others

References

  • Adorio EP (2005) MVF–multivariate test functions library in C for unconstrained global optimization. http://geocities.com/eadorio/mvf.pdf

  • Baeck T, Hoffmeister F, Schwefel HP (1991) A survey of evolution strategies. In: Proceedings fourth international conference on genetic algorithms. Morgan Kaufmann, San Mateo, pp 2–9

  • Balázs K, Botzheim J, Kóczy LT (2010) Comparison of various evolutionary and memetic algorithms. In: Integrated uncertainty management and applications. Springer, Berlin, pp 431–442

  • Bersini H, Dorigo M, Langerman S, Seront G, Gambardella L (1996) Results of the first international contest on evolutionary optimisation (1st ICEO). In: Proceedings of IEEE international conference evolutionary computation. IEEE Press, Nagoya, Japan, pp 611–615

  • Blackwell T, Branke J (2004) Multi-swarm optimization in dynamic environments, applications of evolutionary computing. In: Raidl GR (ed) Lecture notes in computer science, vol 3005. Springer, Berlin, pp 489–500

  • Bonabeau E, Dorigo M, Theraulaz G (1999) Swarm intelligence: from natural to artificial systems. Oxford University Press, New York

    MATH  Google Scholar 

  • Dorigo M, Maniezzo V, Colorni A (1996) Ant system: optimization by a colony of cooperating agents. IEEE Trans Syst Man Cybern Part B 26(1):29–41

    Article  Google Scholar 

  • Dréo J, Siarry P (2004) Continuous interacting ant colony algorithm based on dense heterarchy. Future Gener Comput Syst 20:841–856

    Article  Google Scholar 

  • El-Abd M (2012) Performance assessment of foraging algorithms vs. evolutionary algorithms. Inf Sci 182(1):243–263

    Article  MathSciNet  Google Scholar 

  • Elbeltagi E, Hegazy T, Grierson D (2005) Comparison among five evolutionary-based optimization algorithms. Adv Eng Inform 19(1):43–53

    Article  Google Scholar 

  • Engelbrecht AP (2005) Fundamentals of computational swarm intelligence. Wiley, Chichester

    Google Scholar 

  • Fogel DB (2000) Evolutionary computation: toward a new philosophy of machine intelligence, 2nd edn. IEEE Press, New York

    Google Scholar 

  • Fogel LJ, Owens AJ, Walsh MJ (1966) Artificial intelligence through simulated evolution. Wiley, New York

    MATH  Google Scholar 

  • García-Nieto J, Alba E (2010) Restart particle swarm optimization with velocity modulation: a scalability test. Soft Comput. doi:10.1007/s00500-010-0648-1. http://sci2s.ugr.es/EAMHCO/pdf-soco/P09.pdf

  • Goldberg DE (1989) Genetic algorithms in search, optimisation and machine learning. Addison Wesley, Reading

    Google Scholar 

  • Herrera F, Lozano M, Molina D (2010) Test suite for the special issue of soft computing on scalability of evolutionary algorithms and other metaheuristics for large scale continuous optimization problems. http://sci2s.ugr.es/eamhco/updated-functions1-19.pdf

  • Holland JH (1975) Adaptation in natural and artificial systems. University of Michigan Press, Ann Arbor

    Google Scholar 

  • Juang CF (2004) A hybrid of genetic algorithm and particle swarm optimization for recurrent network design. IEEE Trans Syst Man Cybern Part B Cybern 34(2):997–1006

    Article  Google Scholar 

  • Karaboga D (2005) An idea based on honey bee swarm for numerical optimization. Technical Report-TR06, Erciyes University, Engineering Faculty, Computer Engineering Department. http://mf.erciyes.edu.tr/abc/pub/tr06_2005.pdf

  • Karaboga D, Akay D (2009) Artificial bee colony, harmony search and bees algorithms on numerical optimization. In: Proceedings of 5th international virtual conference on intelligent production machines and systems (IPROMS 2009). Whittles, Dunbeath, Scotland, pp 417–422

  • Karaboga D, Basturk B (2008) On the performance of artificial bee colony (ABC) algorithm. Appl Soft Comput 8(1):687–697

    Article  Google Scholar 

  • Kennedy J (2006) Swarm intelligence, handbook of nature-inspired and innovative computing. In: Zomaya A (ed). Springer, USA, pp 187–219

  • Kennedy J, Eberhart R (1995) Particle swarm optimization. In: Proceedings of 1995 IEEE international conference on neural networks, Perth, Australia, vol 4. IEEE Press, New York, NY, pp 1942– 1948

  • Koza JR (1992) Genetic Programming: on the programming of computers by means of natural selection. MIT Press, Cambridge

    MATH  Google Scholar 

  • Liao T, Montes de Oca MA, Aydin DG, Stuetzle T, Dorigo M (2011) An incremental ACOR with local search for continuous optimization problems. IRIDIA Technical report number TR/IRIDIA/2011-005. http://iridia.ulb.ac.be/IridiaTrSeries/IridiaTr2011-005r001.pdf

  • MacNish C (2007) Towards unbiased benchmarking of evolutionary and hybrid algorithms for real-valued optimisation. Connect Sci 19(4):361–385

    Article  Google Scholar 

  • Mehrabian AR, Lucas C (2006) A novel numerical optimization algorithm inspired from weed colonization. Ecol Inf 1(4):355–366

    Article  Google Scholar 

  • Mengshoel OJ, Goldberg DE (2008) The crowding approach to niching in genetic algorithms. Evol Comput 16(3):315–354

    Article  Google Scholar 

  • Molga M, Smutnicki C (2005) Test functions for optimization needs. http://www.zsd.ict.pwr.wroc.pl/files/docs/functions.pdf

  • Monson CK, Seppi KD (2005) Exposing origin-seeking Bias in PSO. In: Proceedings of 2005 genetic and evolutionary computation conference (GECCO), Washington, DC. ACM Press, New York, NY, pp 241–248

  • Olague G, Puente C (2006) Parisian evolution with honeybees for three-dimensional reconstruction. In: Proceedings of 2006 genetic and evolutionary computation conference (GECCO). ACM Press, New York, NY, pp 191–198

  • Passino KM (2002) Biomimicry of bacterial foraging for distributed optimisation and control. IEEE Control Syst Mag (June), pp 52– 67

  • Pham DT, Castellani M (2009) The bees algorithm—modelling foraging behaviour to solve continuous optimisation problems. Proc ImechE Part C 223(12):2919–2938

    Article  Google Scholar 

  • Pham DT, Castellani M (2010) Adaptive selection routine for evolutionary algorithms. J Syst Control Eng 224(16):623–633

    Google Scholar 

  • Pham DT, Sholedolu M (2008), Using a hybrid PSO-bees algorithm to train neural networks for wood defect classification. In: Proceedings of 4th international virtual conference on intelligent production machines and systems (IPROMS 2008), Whittles, Dunbeath, Scotland, pp 385–390

  • Pham DT, Ghanbarzadeh A, Koc E, Otri S, Rahim S, Zaidi M (2005) The bees algorithm. Manufacturing Engineering Centre, Cardiff University, UK. Technical Note

  • Pham DT, Ghanbarzadeh A, Koç E, Otri S, Rahim S, Zaidi M (2006) The bees algorithm, a novel tool for complex optimisation problems. In: Proceedings of 2nd international virtual conference on intelligent production machines and systems (IPROMS 2006). Elsevier, Oxford, pp 454–459

  • Rechenberg I (1965) Cybernetic solution path of an experimental problem, library translation no. 1122, Ministry of Aviation, Royal Aircraft Establishment, Farnborough, Hants, UK

  • Roth M, Wicker S (2003) Termite: ad-hoc networking with stigmergy. In: Proceedings of global telecommunications conference GLOBECOM ’03, vol 5. IEEE press, San Francisco, CA, pp 2937–2941

  • Sato T, Hagiwara M (1997) Bee system: finding solution by a concentrated search. In: Proceedings of IEEE international conference systems, Man, & Cybernetics. IEEE Press, New York, NY, pp 3954–3959

  • Shi Y, Eberhart R (1998) Parameter selection in particle swarm optimization. In: Proceedings of seventh annual conference on evolutionary programming, San Diego, CA, Lecture Notes in Computer Science volume 1447, Springer, Berlin, pp 591–600

  • Shi XH, Lu YH, Zhou CG, Lee HP, Lin WZ, Liang YC (2003) Hybrid evolutionary algorithms based on PSO and GA. In: Proceedings IEEE congress Evolutionary computation, Canberra, Australia. IEEE Press, Piscataway, NJ, pp 2393–2399

  • Socha K, Dorigo M (2008) Ant colony optimisation for continuous domains. Eur J Oper Res 185:1155–1173

    Article  MATH  MathSciNet  Google Scholar 

  • Storn R, Price K (1997) Differential evolution—a simple and efficient heuristic for global optimization over continuous spaces. J Glob Optim 11:341–359

    Google Scholar 

  • Suganthan PN, Hansen N, Liang JJ, Deb K, Chen YP, Auger A, Tiwari S (2005) Problem definitions and evaluation criteria for the CEC, special session on real-parameter optimization. KanGAL Report 2005005:2005

  • Tang K, Yao X, Suganthan PN, MacNish C, Chen YP, Chen CM, Yang Z (2007) Benchmark functions for the CEC’2008 special session and competition on large scale global optimization. Technical report, Nature Inspired Computation and Applications Laboratory, USTC, Hefei, Anhui, China. http://nical.ustc.edu.cn/cec08ss.php

  • Tang K, Li X, Suganthan PN, Yang Z, Weise T (2009) Benchmark functions for the CEC’2010 special session and competition on large scale global optimization. Technical report, Nature Inspired Computation and Applications Laboratory, USTC, Hefei, Anhui, China., http://nical.ustc.edu.cn/cec10ss.php

  • Wolpert DH, Macready WG (1997) No free lunch theorems for optimization. IEEE Trans Evol Comput 1(1):67–82

    Article  Google Scholar 

  • Yang XS (2008) Nature-inspired metaheuristic algorithms. Luniver Press, UK

  • Yang XS, Deb S (2010) Engineering optimisation by cuckoo search. Int J Math Model Numer Optim 1(4):330–343

    MATH  Google Scholar 

  • Zapfel G, Braune R, Bogl M (2010) Metaheuristic search concepts. Springer, Berlin

Download references

Author information

Authors and Affiliations

  1. School of Mechanical Engineering, University of Birmingham, Birmingham, B15 2TT, UK

    D. T. Pham

  2. Department of Biology, University of Bergen, Postboks 7803, 5020 , Bergen, Norway

    M. Castellani

Authors
  1. D. T. Pham
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. M. Castellani
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to M. Castellani.

Additional information

Communicated by R. John.

Appendices

Appendix A: Optimisation benchmarks

1.1 General features

All functions are defined within the interval:

\(I =\{x\in \mathrm{R}^\mathrm{n}; -100<x_{i}<100, i=1,2,\ldots ,n\}.\)

All but functions 22, 23, and 24 are two-dimensional.

For all functions, \(f(x^{\mu })=0\) where \(x^{\mu }=(x^{\mu }_{1},\ldots ,x^{\mu }_{n})\) is the global minimum point.

1.2 Multimodal functions

1.2.1 Function 1

This function maps two “holes”. The global optimum is located at the origin of the search space.

$$\begin{aligned} f( {x_1 ,x_2 })&= 1.0-0.8\cdot e^{-\left( {\frac{^{\left( {( {x_1 -50})^2+( {x_2 -50})^2}\right) }}{200}}\right) }\\&-1.0\cdot e^{-\left( {\frac{^{\left( {( {x_1 -0})^2+( {x_2 -0})^2}\right) }}{200}}\right) }\\ x^\mu&= (0,0) \end{aligned}$$

1.2.2 Function 2

This function maps two “holes”. The global optimum is located far from the origin of the search space.

$$\begin{aligned} f( {x_1 ,x_2 })&= 1.0-1.0\cdot e^{-\left( {\frac{^{\left( {( {x_1 -50})^2+( {x_2 -50})^2}\right) }}{200}}\right) }\\&-0.8\cdot e^{-\left( {\frac{^{\left( {( {x_1 -0})^2+( {x_2 -0})^2}\right) }}{200}}\right) }\\&x^\mu =(50,50) \end{aligned}$$

1.2.3 Function 3

This function maps nine basins of equal size arranged on a grid. The global minimum corresponds to one of the lateral basins of the grid.

$$\begin{aligned}&f( {x_1 ,x_2 })=1.0-0.8\cdot e^{-\left( {\frac{^{( {x_1 -60})^2+( {x_2 -60})^2}}{100}}\right) }\\&\quad -1.0\cdot e^{-\left( {\frac{^{( {x_1 -0})^2+( {x_2 -60})^2}}{100}}\right) }-0.8\cdot e^{-\left( {\frac{^{( {x_1 +60})^2+( {x_2 -60})^2}}{100}}\right) } \\&\quad -0.8\cdot e^{-\left( {\frac{^{( {x_1 -60})^2+( {x_2 -0})^2}}{100}}\right) }-0.8\cdot e^{-\left( {\frac{^{( {x_1 -0})^2+( {x_2 -0})^2}}{100}}\right) }\\&\quad -0.8\cdot e^{-\left( {\frac{^{( {x_1 +60})^2+( {x_2 -0})^2}}{100}}\right) } \\&\quad -0.8\cdot e^{-\left( {\frac{^{( {x_1 -60})^2+( {x_2 +60})^2}}{100}}\right) }-0.8\cdot e^{-\left( {\frac{^{( {x_1 -0})^2+( {x_2 +60})^2}}{100}}\right) }\\&\quad -0.8\cdot e^{-\left( {\frac{^{( {x_1 +60})^2+( {x_2 +60})^2}}{100}}\right) } \\&x^\mu =(0,60) \end{aligned}$$

1.2.4 Function 4

This function describes the same fitness landscape of function 3 rotated of 4/9\(\cdot \pi \).

$$\begin{aligned}&f( {r_1 ,r_2 })=1.0-0.8\cdot e^{-\left( {\frac{^{( {r_1 -60})^2+( {r_2 -60})^2}}{100}}\right) }\\&\quad -1.0\cdot e^{-\left( {\frac{^{( {r_1 -0})^2+( {r_2 -60})^2}}{100}}\right) }-0.8\cdot e^{-\left( {\frac{^{( {r_1 +60})^2+( {r_2 -60})^2}}{100}}\right) } \\&\quad -0.8\cdot e^{-\left( {\frac{^{( {r_1 -60})^2+( {r_2 -0})^2}}{100}}\right) }-0.8\cdot e^{-\left( {\frac{^{( {r_1 -0})^2+( {r_2 -0})^2}}{100}}\right) }\\&\quad -0.8\cdot e^{-\left( {\frac{^{( {r_1 +60})^2+( {r_2 -0})^2}}{100}}\right) } \\&\quad -0.8\cdot e^{-\left( {\frac{^{( {r_1 -60})^2+( {r_2 +60})^2}}{100}}\right) }\\&\quad -0.8\cdot e^{-\left( {\frac{^{( {r_1 -0})^2+( {r_2 +60})^2}}{100}}\right) }\\&\quad -0.8\cdot e^{-\left( {\frac{^{( {r_1 +60})^2+( {r_2 +60})^2}}{100}}\right) } \\&r_1 =x_1 \cdot \cos \left( {\frac{4}{9}\cdot \pi }\right) -x_2 \cdot \sin \left( {\frac{4}{9}\cdot \pi }\right) \\&r_2 =x_1 \cdot \sin \left( {\frac{4}{9}\cdot \pi }\right) +x_2 \cdot \cos \left( {\frac{4}{9}\cdot \pi }\right) \\&x^\mu =(-25.7,-54.2) \end{aligned}$$

1.2.5 Function 5

This function maps eleven large secondary basins, and a narrow and steep hole near the top-right corner of the search space where the global minimum is located. The secondary minima are arranged on a grid.

$$\begin{aligned}&f( {x_1 ,x_2 })=1.0-1.0\cdot e^{-\left( {\frac{^{( {x_1 -80})^2+( {x_2 -80})^2}}{100}}\right) ^4}\\&\quad -0.75\cdot e^{-\left( {\frac{^{( {x_1 +50})^2+( {x_2 +50})^2}}{400}}\right) } \\&\quad +-0.75\cdot e^{-\left( {\frac{^{( {x_1 +50})^2+( {x_2 -50})^2}}{400}}\right) }-0.75\cdot e^{-\left( {\frac{^{( {x_1 -50})^2+( {x_2 +50})^2}}{400}}\right) }\\&\quad -0.75\cdot e^{-\left( {\frac{^{( {x_1 +0})^2+( {x_2 +50})^2}}{400}}\right) } \\&\quad +-0.75\cdot e^{-\left( {\frac{^{( {x_1 +0})^2+( {x_2 -50})^2}}{400}}\right) }-0.75\cdot e^{-\left( {\frac{^{( {x_1 +50})^2+( {x_2 +0})^2}}{400}}\right) }\\&\quad -0.75\cdot e^{-\left( {\frac{^{( {x_1 -50})^2+( {x_2 +0})^2}}{400}}\right) } \\&\quad +-0.75\cdot e^{-\left( {\frac{^{( {x_1 +100})^2+( {x_2 +100})^2}}{400}}\right) }\\&\quad -0.75\cdot e^{-\left( {\frac{^{( {x_1 -100})^2+( {x_2 +100})^2}}{400}}\right) }\\&\quad -0.75\cdot e^{-\left( {\frac{^{( {x_1 +100})^2+( {x_2 -100})^2}}{400}}\right) } \\&\quad +-0.75\cdot e^{-\left( {\frac{^{( {x_1 +0})^2+( {x_2 +0})^2}}{400}}\right) } \\&x^\mu =(80,80) \end{aligned}$$

1.2.6 Function 6

This function maps eleven large secondary basins, and a narrow and steep hole at the origin of the search space where the global minimum is located. The secondary minima are arranged on a grid.

$$\begin{aligned}&f( {x_1 ,x_2 })=1.0-1.0\cdot e^{-\left( {\frac{^{( {x_1 -0})^2+( {x_2 -0})^2}}{100}}\right) ^4}\\&\quad -0.75\cdot e^{-\left( {\frac{^{( {x_1 +50})^2+( {x_2 +50})^2}}{400}}\right) } \\&\quad +-0.75\cdot e^{-\left( {\frac{^{( {x_1 +50})^2+( {x_2 -50})^2}}{400}}\right) }-0.75\cdot e^{-\left( {\frac{^{( {x_1 -50})^2+( {x_2 +50})^2}}{400}}\right) }\\&\quad -0.75\cdot e^ {-\left( {\frac{^{( {x_1 -50})^2+( {x_2 -50})^2}}{400}}\right) } \\&\quad +-0.75\cdot e^{-\left( {\frac{^{( {x_1 +0})^2+( {x_2 +50})^2}}{400}}\right) }-0.75\cdot e^{-\left( {\frac{^{( {x_1 +0})^2+( {x_2 -50})^2}}{400}}\right) }\\&\quad -0.75\cdot e^{-\left( {\frac{^{( {x_1 +50})^2+( {x_2 +0})^2}}{400}}\right) } \\&\quad +-0.75\cdot e^{-\left( {\frac{^{( {x_1 -50})^2+( {x_2 +0})^2}}{400}}\right) }-0.75\cdot e^{-\left( {\frac{^{( {x_1 +100})^2+( {x_2 +100})^2}}{400}}\right) }\\&\quad -0.75\cdot e^{-\left( {\frac{^{( {x_1 -100})^2+( {x_2 +100})^2}}{400}}\right) } \\&\quad +-0.75\cdot e^{-\left( {\frac{^{( {x_1 +100})^2+( {x_2 -100})^2}}{400}}\right) } \\&x^\mu =(0,0) \end{aligned}$$

1.2.7 Function 7

This function maps eleven large secondary basins, and a narrow and steep hole near the top-right corner of the search space where the global minimum is located. The secondary minima are not arranged on a grid.

$$\begin{aligned}&f( {x_1 ,x_2 })=1.0-1.0\cdot e^{-\left( {\frac{^{( {x_1 -85})^2+( {x_2 -80})^2}}{100}}\right) ^4}\\&\quad -0.75\cdot e^{-\left( {\frac{^{( {x_1 +65})^2+( {x_2 +45})^2}}{400}}\right) } \\&\quad +-0.75\cdot e^{-\left( {\frac{^{( {x_1 -40})^2+( {x_2 +70})^2}}{400}}\right) }\\&\quad -0.75\cdot e^{-\left( {\frac{^{( {x_1 +50})^2+( {x_2 -80})^2}}{400}}\right) }\\&\quad -0.75\cdot e^{-\left( {\frac{^{( {x_1 +0})^2+( {x_2 +55})^2}}{400}}\right) } \\&\quad +-0.75\cdot e^{-\left( {\frac{^{( {x_1 +15})^2+( {x_2 -60})^2}}{400}}\right) }\\&\quad -0.75\cdot e^{-\left( {\frac{^{( {x_1 +65})^2+( {x_2 -10})^2}}{400}}\right) }-0.75\cdot e^{-\left( {\frac{^{( {x_1 -80})^2+( {x_2 +5})^2}}{400}}\right) } \\&\quad +-0.75\cdot e^{-\left( {\frac{^{( {x_1 +0})^2+( {x_2 +0})^2}}{400}}\right) } -0.75\cdot e^{-\left( {\frac{^{( {x_1 -70})^2+( {x_2 +90})^2}}{400}}\right) }\\&\quad -0.75\cdot e^{-\left( {\frac{^{( {x_1 +95})^2+( {x_2 -90})^2}}{400}}\right) } \\&\quad +-0.75\cdot e^{-\left( {\frac{^{( {x_1 +85})^2+( {x_2 +80})^2}}{400}}\right) } \\&\quad x^\mu =(85,80) \end{aligned}$$

1.2.8 Function 8

This function maps eleven large secondary basins, and a narrow and steep hole at the origin of the search space where the global minimum is located. The secondary minima are not arranged on a grid.

$$\begin{aligned}&f( {x_1 ,x_2 })=1.0-1.0\cdot e^{-\left( {\frac{^{( {x_1 -0})^2+( {x_2 -0})^2}}{100}}\right) ^4}\\&\quad -0.75\cdot e^{-\left( {\frac{^{( {x_1 -65})^2+( {x_2 -45})^2}}{400}}\right) } \\&\quad +-0.75\cdot e^{-\left( {\frac{^{( {x_1 -40})^2+( {x_2 +70})^2}}{400}}\right) }-0.75\cdot e^{-\left( {\frac{^{( {x_1 +75})^2+( {x_2 +35})^2}}{400}}\right) }\\&\quad -0.75\cdot e^{-\left( {\frac{^{( {x_1 +50})^2+( {x_2 -80})^2}}{400}}\right) } \\&\quad +-0.75\cdot e^{-\left( {\frac{^{( {x_1 +0})^2+( {x_2 +55})^2}}{400}}\right) }-0.75\cdot e^{-\left( {\frac{^{( {x_1 +15})^2+( {x_2 -60})^2}}{400}}\right) }\\&\quad -0.75\cdot e^{-\left( {\frac{^{( {x_1 +65})^2+( {x_2 -10})^2}}{400}}\right) } \\&\quad +-0.75\cdot e^{-\left( {\frac{^{( {x_1 -80})^2+( {x_2 +5})^2}}{400}}\right) }-0.75\cdot e^{-\left( {\frac{^{( {x_1 -70})^2+( {x_2 +90})^2}}{400}}\right) }\\&\quad -0.75\cdot e^{-\left( {\frac{^{( {x_1 +85})^2+( {x_2 +80})^2}}{400}}\right) } \\&\quad +-0.75\cdot e^{-\left( {\frac{^{( {x_1 +90})^2+( {x_2 -70})^2}}{400}}\right) } \\&x^\mu =(0,0) \end{aligned}$$

1.3 Minimum surrounded by flat surface

1.3.1 Function 9

This function maps a multimodal search surface. The global minimum lies at the origin of the search space, and its basin is characterised by a large flat step and a steep and narrow ending. Four secondary minima are arranged on a grid.

$$\begin{aligned}&f( {x_1 ,x_2 })= \left\{ \begin{array}{l} ( {( {x_1 +0})^2+( {x_2 +0})^2\le 625})\Rightarrow 0.4-0.4\cdot e^{-\left( {\frac{( {x_1 +0})^2+( {x_2 +0})^2}{10}}\right) } \\ else\Rightarrow 1.0-0.75\cdot e^{-\left( {\frac{^{\left( {x_1 +75}\right) ^2+\left( {x_2 +75}\right) ^2}}{1000}}\right) }\\ -0.75\cdot e^{-\left( {\frac{^{( {x_1 -75})^2+( {x_2-75})^2}}{1000}}\right) } \\ +-0.75\cdot e^{-\left( {\frac{^{( {x_1 -75})^2+( {x_2 +75})^2}}{1000}}\right) }\\ -0.75\cdot e^{-\left( {\frac{^{( {x_1 +75})^2+( {x_2 -75})^2}}{1000}}\right) } \\ +-0.75\cdot e^{-\left( {\frac{^{( {x_1 +0})^2+( {x_2 +0})^2}}{1000}}\right) } \\ \end{array}\right. \\&x^\mu =(0,0) \end{aligned}$$

1.3.2 Function 10

This function maps a multimodal search surface. The global minimum lies far from the origin of the search space, and its basin is characterised by a large flat step and a steep and narrow ending. Four secondary minima are arranged on a grid.

$$\begin{aligned}&f( {x_1 ,x_2 })= \left\{ \begin{array}{l} ( {( {x_1 +75})^2+( {x_2 +75})^2\le 625})\Rightarrow 0.4-0.4\cdot e^{-\left( {\frac{( {x_1 +75})^2+( {x_2 +75})^2}{10}}\right) } \\ else\Rightarrow 1.0-0.75\cdot e^{-\left( {\frac{^{( {x_1 +75})^2+( {x_2 +75})^2}}{1000}}\right) }\\ -0.75\cdot e^{-\left( {\frac{^{( {x_1 -75})^2+( {x_2 -75})^2}}{1000}}\right) } \\ +-0.75\cdot e^{-\left( {\frac{^{( {x_1 -75})^2+( {x_2 +75})^2}}{1000}}\right) }\\ -0.75\cdot e^{-\left( {\frac{^{( {x_1 +75})^2+( {x_2 -75})^2}}{1000}}\right) } \\ +-0.75\cdot e^{-\left( {\frac{^{( {x_1 +0})^2+( {x_2 +0})^2}}{1000}}\right) } \\ \end{array}\right. \\&x^\mu =(-75,-75) \end{aligned}$$

1.3.3 Function 11

This function maps a multimodal search surface. The global minimum lies at the origin of the search space, and its basin is characterised by a large flat step and a steep and narrow ending. Four secondary minima are not arranged on a grid.

$$\begin{aligned}&f( {x_1 ,x_2 })=\left\{ {\begin{array}{l} ( {( {x_1 +0})^2+( {x_2 +0})^2\le 625})\Rightarrow 0.4-0.4\cdot e^{-\left( {\frac{( {x_1 +0})^2+( {x_2 +0})^2}{10}}\right) } \\ else\Rightarrow 1.0-0.75\cdot e^{-\left( {\frac{^{( {x_1 +75})^2+( {x_2 +75})^2}}{1000}}\right) }\\ -0.75\cdot e^{-( {\frac{^{( {x_1 -50})^2+( {x_2 -60})^2}}{1000}})} \\ +-0.75\cdot e^{-\left( {\frac{^{( {x_1 -70})^2+( {x_2 +55})^2}}{1000}}\right) }\\ -0.75\cdot e^{-\left( {\frac{^{( {x_1 +45})^2+( {x_2 -85})^2}}{1000}}\right) } \\ +-0.75\cdot e^{-\left( {\frac{^{( {x_1 +0})^2+( {x_2 +0})^2}}{1000}}\right) } \\ \end{array}} \right. \\&x^\mu =(0,0) \end{aligned}$$

1.3.4 Function 12

This function maps a multimodal search surface. The global minimum lies far from the origin of the search space, and its basin is characterised by a large flat step and a steep and narrow ending. Four secondary minima are not arranged on a grid.

$$\begin{aligned}&f( {x_1 ,x_2 })=\left\{ {\begin{array}{l} ( {( {x_1 +75})^2+( {x_2 +75})^2\le 625})\Rightarrow 0.4-0.4\cdot e^{-\left( {\frac{( {x_1 +75})^2+( {x_2 +75})^2}{10}}\right) } \\ else\Rightarrow 1.0-0.75\cdot e^{-\left( {\frac{^{( {x_1 +75})^2+( {x_2 +75})^2}}{1000}}\right) }\\ -0.75\cdot e^{-\left( {\frac{^{( {x_1 -50})^2+( {x_2 -60})^2}}{1000}}\right) } \\ +-0.75\cdot e^{-\left( {\frac{^{( {x_1 -70})^2+( {x_2 +55})^2}}{1000}}\right) }\\ -0.75\cdot e^{-\left( {\frac{^{( {x_1 +45})^2+( {x_2 -85})^2}}{1000}}\right) } \\ +-0.75\cdot e^{-\left( {\frac{^{( {x_1 +0})^2+( {x_2 +0})^2}}{1000}}\right) } \\ \end{array}} \right. \\&x^\mu =(-75,-75) \end{aligned}$$

1.4 Narrow valleys

1.4.1 Function 13

This function maps two valleys on opposite sides of the search space.

$$ \begin{aligned}&f( {x_1 ,x_2 })=\left\{ {\begin{array}{l} ( {x_1 \ge 0 \& x_2 \ge 0}) \Rightarrow 1.0-0.75\cdot e^{-\left( {\frac{^{( {x_2 -50})^2}}{50}}\right) } \\ ( {x_1 <0 \& x_2 <0}) \Rightarrow 1.0-1.0\cdot \left( {\frac{x_2 +100}{70}}\right) \cdot e^{-\left( {\frac{^{( {x_1 +x_2 +130})^2}}{25}}\right) } \\ \end{array}} \right. \\&x^\mu =(-100,-30) \end{aligned}$$

1.4.2 Function 14

This function maps two pairs of valleys of opposite slopes that represent competing basins of attraction. The minimum is located near the borders of the search surface at the end of the narrowest valley. The four valleys join at the origin, where a further basin is located.

$$\begin{aligned}&f( {x_1 ,x_2 })=1.0-1.0\cdot e^{-\left( {\frac{^{x_1 -90}}{25}}\right) ^2}\cdot e^{-\left( {\frac{( {x_1 +2\cdot x_2 })^2}{2}}\right) }\\&\quad -0.75\cdot e^{-\left( {\frac{^{x_1 +100}}{25}}\right) ^2}\cdot e^{-\left( {\frac{( {x_1 +2\cdot x_2 })^2}{1000}}\right) } \\&\quad +-0.80\cdot e^{-\left( {\frac{^{( {x_1 +0})^2+( {x_2 +0})^2}}{150}}\right) }\\&\quad -0.75\cdot \left( {\frac{x_2 }{100}}\right) ^2\cdot \\&\quad e^{-\left( {\frac{^{( {3\cdot x_1 -x_2 })^2}}{1000}}\right) }\\&x^\mu =(90,-45) \end{aligned}$$

1.4.3 Function 15

This function maps a narrow parabolic valley surrounded by a large flat surface. The valley is located in the half plane of positive x1 values (x1 \(>\) 0). The other half of the fitness landscape is covered by a sliding plane.

$$\begin{aligned}&f( {x_1, x_2 })=\left\{ {\begin{array}{l} ( {x_1 \ge 0})\Rightarrow 1.0-\frac{x_1^4 }{90^4}\cdot e^{-\left( {\frac{^{\left( {x_1^2 +4\cdot x_2^2 -8100}\right) ^2}}{250}}\right) } \\ else\Rightarrow 1.0-\frac{x_1 }{125} \\ \end{array}} \right. \\&x^\mu =( {90,0}) \end{aligned}$$

1.5 Wavelike

1.5.1 Function 16

This function combines two cosinusoidal functions. Each function depends on one of the two input variables, and its amplitude increases linearly with the associated variable. The global minimum is in a narrow hole that is added to one of the “pockets” of the search surface. Function 16 has an overall unimodal characteristic corresponding to a plane slanted toward the positive values of the two input variables. The optimum is far from the origin and does not correspond to the minimum of the unimodal characteristic (i.e. the slanted plane).

$$\begin{aligned} f( {x_1, x_2 })&= 1.0-\left( {0.4+0.4\cdot \cos \left( {2\cdot \pi \cdot \frac{x_1 -75}{25}}\right) }\right) \\&\cdot \frac{x_1 +100}{400} \\&-\left( {0.4+0.4\cdot \cos \left( {2\cdot \pi \cdot \frac{x_2 -75}{25}}\right) }\right) \\&\cdot \frac{x_2 +100}{400}-0.30\cdot e^{-\left( {\frac{^{( {x_1 -75})^2+( {x_2 -75})^2}}{10}}\right) } \\ x^\mu&= (75,75) \end{aligned}$$

1.5.2 Function 17

This function combines two sinusoidal functions. The two functions have constant amplitude and variable period. The global minimum is in a narrow hole that is added to one of the “pockets” of the search surface.

$$\begin{aligned}&f( {x_1 ,x_2 })=1.0-0.2+0.2\cdot \\&\quad \sin \left( {2+\frac{x_2 +100}{100}\cdot \pi \cdot \frac{x_1 }{50}}\right) \\&\quad +-0.2+0.2\cdot \sin \left( {2+\frac{x_1 +100}{100}\cdot \pi \cdot \frac{x_2 }{50}}\right) -0.2\\&\quad \cdot e^{-\left( {\frac{^{( {x_1 -50})^2+( {x_2 -50})^2}}{10}}\right) } \\&x^\mu =(50,50) \end{aligned}$$

1.6 “Noisy” unimodal

1.6.1 Function 18

This function has overall unimodal behaviour with a cosinusoidal noise component. The magnitude of the noise component corresponds to 10 % of that of the unimodal curve. The peak lies far from the origin.

$$\begin{aligned}&f( {x_1 ,x_2 })=1.0-0.3\cdot \left( {\left( {\frac{x_1 -50}{50}}\right) ^2+\left( {\frac{x_2 -50}{50}}\right) ^2+1}\right) \\&-0.3\cdot \left( {\left( {\frac{x_1 -50}{25}}\right) ^2+\left( {\frac{x_2 -50}{25}}\right) ^2+1}\right) \\&-0.3\cdot \left( {\left( {\frac{x_1 -50}{10}}\right) ^2+\left( {\frac{x_2 -50}{10}}\right) ^2+1}\right) \\&-0.05\cdot \left| {\cos ( {2\cdot \pi \cdot ( {x_1 -50})})+\cos ( {2\cdot \pi \cdot ( {x_2 -50})})} \right| \\&x^\mu =(50,50) \end{aligned}$$

1.6.2 Function 19

This function has an overall unimodal behaviour with a cosinusoidal noise component. The magnitude of the noise component corresponds to 25 % of that of the unimodal curve. The peak lies far from the origin.

$$\begin{aligned}&f( {x_1 ,x_2 })=1.0-0.25\cdot \left( {\left( {\frac{x_1 -50}{50}}\right) ^2+\left( {\frac{x_2 -50}{50}}\right) ^2+1}\right) \\&-0.25\cdot \left( {\left( {\frac{x_1 -50}{25}}\right) ^2+\left( {\frac{x_2 -50}{25}}\right) ^2+1}\right) \\&-0.25\cdot \left( {\left( {\frac{x_1 -50}{10}}\right) ^2+\left( {\frac{x_2 -50}{10}}\right) ^2+1}\right) \\&-0.125\cdot \left| {\cos ( {2\cdot \pi \cdot ( {x_1 -50})})+\cos ( {2\cdot \pi \cdot ( {x_2 -50})})} \right| \\&x^\mu =(50,50) \end{aligned}$$

1.6.3 Function 20

This function has an overall unimodal behaviour with a cosinusoidal noise component. The magnitude of the noise component corresponds to 40 % of that of the unimodal curve. The peak lies far from the origin.

$$\begin{aligned}&f( {x_1 ,x_2 })=1.0-0.2\cdot \left( {\left( {\frac{x_1 -50}{50}}\right) ^2+\left( {\frac{x_2 -50}{50}}\right) ^2+1}\right) \\&\quad -0.2\cdot \left( {\left( {\frac{x_1 -50}{25}}\right) ^2+\left( {\frac{x_2 -50}{25}}\right) ^2+1}\right) \\&\quad -0.2\cdot \left( {\left( {\frac{x_1 -50}{10}}\right) ^2+\left( {\frac{x_2 -50}{10}}\right) ^2+1}\right) \\&\quad -0.2\cdot \left| {\cos ( {2\cdot \pi \cdot ( {x_1 -50})})+\cos ( {2\cdot \pi \cdot ( {x_2 -50})})} \right| \\&x^\mu =(50,50) \end{aligned}$$

1.6.4 Function 21

This function is similar to function 19 but the period of the cosinusoidal noise component is multiplied by a factor 4.

$$\begin{aligned}&f( {x_1 ,x_2 })=1.0-0.25\cdot \left( {\left( {\frac{x_1 -50}{50}}\right) ^2+\left( {\frac{x_2 -50}{50}}\right) ^2+1}\right) \\&\quad -0.25\cdot \left( {\left( {\frac{x_1 -50}{25}}\right) ^2+\left( {\frac{x_2 -50}{25}}\right) ^2+1}\right) \\&\quad -0.25\cdot \left( {\left( {\frac{x_1 -50}{10}}\right) ^2+\left( {\frac{x_2 -50}{10}}\right) ^2+1}\right) \\&\quad -0.125\cdot \left| {\cos \left( {2\cdot \pi \cdot \frac{( {x_1 -50})}{4}}\right) +\cos \left( {2\cdot \pi \cdot \frac{( {x_2 -50})}{4}}\right) } \right| \\&x^\mu =(50,50) \end{aligned}$$

1.6.5 Function 22

This function is similar to function 19 but the period of the cosinusoidal noise component is divided by a factor 4.

$$\begin{aligned}&f( {x_1 ,x_2 })=1.0-0.25\cdot \left( {\left( {\frac{x_1 -50}{50}}\right) ^2+\left( {\frac{x_2 -50}{50}}\right) ^2+1}\right) \\&-0.25\cdot \left( {\left( {\frac{x_1 -50}{25}}\right) ^2+\left( {\frac{x_2 -50}{25}}\right) ^2+1}\right) \\&-0.25\cdot \left( {\left( {\frac{x_1 -50}{10}}\right) ^2+\left( {\frac{x_2 -50}{10}}\right) ^2+1}\right) \\&-0.125\cdot \left| {\cos ( {2\cdot \pi \cdot 4\cdot ( {x_1 -50})})+\cos ( {2\cdot \pi \cdot 4\cdot ( {x_2 -50})})} \right| \\&x^\mu =(50,50) \end{aligned}$$

1.7 Different dimensionality

1.7.1 Function 23

This function maps seven secondary basins, and the global minimum is located far from the origin. The secondary minima are not arranged on a grid. The function is ten-dimensional

$$\begin{aligned}&f( {x_1 ,\ldots ,x_{10} })=1.0-1.0\cdot e^{\sum \nolimits _{i=1}^{10} {( {x_i -75})^2} }\\&-\sum \limits _{j=0}^6 {0.8\cdot e^{\frac{\sum \nolimits _{i=1}^{10} {-( {x_i +sign_{ij} \cdot j\cdot 15})^2} }{2000}}} \\&sign_{ij} =2\cdot \min \left( {1,\frac{i+1}{j+1}}\right) -1 \\&x^\mu =(75,\ldots ,75) \end{aligned}$$

1.7.2 Function 24

This function maps seven secondary basins, and the global minimum is located far from the origin. The secondary minima are not arranged on a grid. The function is fifteen-dimensional

$$\begin{aligned}&f( {x_1 ,\ldots ,x_{15} })=1.0-1.0\cdot e^{\sum \nolimits _{i=1}^{15} {( {x_i -75})^2} }\\&-\sum \limits _{j=0}^6 {0.8\cdot e^{\frac{\sum \nolimits _{i=1}^{15} {-( {x_i +sign_{ij} \cdot j\cdot 15})^2} }{2000}}} \\&sign_{ij} =2\cdot \min \left( {1,\frac{i+1}{j+1}}\right) -1 \\&x^\mu =(75,\ldots ,75) \end{aligned}$$

1.7.3 Function 25

This function maps seven secondary basins, and the global minimum is located far from the origin. The secondary minima are not arranged on a grid. The function is twenty-dimensional

$$\begin{aligned}&f( {x_1 ,\ldots ,x_{20} })=1.0-1.0\cdot e^{\sum \nolimits _{i=1}^{20} {( {x_i -75})^2} }\\&\quad -\sum \limits _{j=0}^6 {0.8\cdot e^{\frac{\sum \nolimits _{i=1}^{20} {-( {x_i +sign_{ij} \cdot j\cdot 15})^2} }{2000}}} \\&\quad sign_{ij} =2\cdot \min \left( {1,\frac{i+1}{j+1}}\right) -1 \\&\quad x^\mu =(75,\ldots ,75) \end{aligned}$$

B: Algorithms configurations

See Tables 15, 16, 17 and 18.

Table 15 EA configurations
Full size table
Table 16 PSO configurations
Full size table
Table 17 ABC configurations
Full size table
Table 18 Bees Algorithm configurations
Full size table

Rights and permissions

Reprints and permissions

About this article

Cite this article

Pham, D.T., Castellani, M. Benchmarking and comparison of nature-inspired population-based continuous optimisation algorithms. Soft Comput 18, 871–903 (2014). https://doi.org/10.1007/s00500-013-1104-9

Download citation

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00500-013-1104-9

Keywords

Search

Navigation