A PROMETHEE-based outranking method for multiple criteria decision analysis with interval type-2 fuzzy sets

Abstract

This paper develops new methods based on the preference ranking organization method for enrichment evaluations (PROMETHEE) that use a signed distance-based approach within the environment of interval type-2 fuzzy sets for multiple criteria decision analysis. The theory of interval type-2 fuzzy sets provides an intuitive and computationally feasible way of addressing uncertain and ambiguous information in decision-making fields. Many studies have developed multiple criteria decision analysis methods in the context of interval type-2 fuzzy sets; most of these methods can be characterized as scoring or compromising models. Nevertheless, the extended versions of outranking methods have not been thoroughly investigated. This paper establishes interval type-2 fuzzy PROMETHEE methods for ranking alternative actions among multiple criteria based on the concepts of signed distance-based generalized criteria and comprehensive preference indices. We develop interval type-2 fuzzy PROMETHEE I and interval type-2 fuzzy PROMETHEE II procedures for partial and complete ranking, respectively, of the alternatives. Finally, the feasibility and applicability of the proposed methods are illustrated by a practical problem of landfill site selection. A comparative analysis is also performed with ordinary fuzzy PROMETHEE methods to validate the effectiveness of the proposed methodology.

Appendix

Definition 6.1

Let $X$ be an ordinary finite nonempty set. Let Int([0, 1]) denote a set of all closed subintervals of [0, 1]. The mapping $A$: $X\rightarrow$ Int([0, 1]) is known as an IT2FS on $X$. All IT2FSs on $X$ are denoted by IT2FS$(X)$.

Definition 6.2

If $A\in \mathrm{IT2FS}(X)$, let $A(x)\!=\![A^{L}(x), A^{U}(x)]$, where $x\in X$ and $0\le A^L(x)\le A^U(x)\le 1$. The two T1FSs $A^{L}: X\rightarrow [0, 1]$ and $A^{U}: X\rightarrow [0, 1]$ are known as the lower and upper fuzzy sets, respectively, with respect to $A$. If $A(x)$ is convex and defined on a closed and bounded interval, then $A$ is known as “an interval type-2 fuzzy number on $X$”.

Definition 6.3

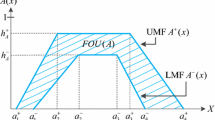
Let $A^L(=(a_1^L, a_2^L, a_3^L, a_4^L ;h_A^L))$ and $A^U(=(a_1^U, a_2^U, a_3^U, a_4^U ;h_A^U))$ be the lower and upper trapezoidal fuzzy numbers defined on the universe of discourse $X$, where $a_1^L \le a_2^L \le a_3^L \le a_4^L$, $a_1^U \le a_2^U \le a_3^U \le a_4^U$, $0\le h_A^L \le h_A^U \le 1$, $a_1^U \le a_1^L$, $a_4^L \le a_4^U$, and $A^L\subset A^U$. Let $\xi \in \{L$, $U\}$. The membership function of $A^\xi$ for each $\xi$ is expressed as follows:

$$\begin{aligned} A^\xi (x)=\left\{ {{\begin{array}{ll} {{h_A^\xi ({x-a_1^\xi })}/{({a_2^\xi -a_1^\xi })}} &{} \quad {\hbox {for } a_1^\xi \le x\le a_2^\xi , } \\ {h_A^\xi } &{} \quad {\hbox {for } a_2^\xi \le x\le a_3^\xi , } \\ {{h_A^\xi ({a_4^\xi -x})}/{({a_4^\xi -a_3^\xi })}} &{} \quad {\hbox {for } a_3^\xi \le x\le a_4^\xi , } \\ 0 &{} \quad {\hbox {otherwise}.} \\ \end{array} }}\right. \nonumber \\ \end{aligned}$$

(36)

An IT2TrFN $A$ on $X$ is represented by the following:

$$\begin{aligned} A&= [A^L, A^U]\nonumber \\&= \left[ {(a_1^L, a_2^L, a_3^L, a_4^L ;h_A^L), (a_1^U , a_2^U, a_3^U, a_4^U ;h_A^U)} \right] . \end{aligned}$$

(37)

The extension principle (Zadeh 1975) can be employed to develop fuzzy arithmetic defined as IT2FSs (Aisbett et al. 2010; Gilan et al. 2012). Let $\oplus$ denote the addition operation, and let $A$ and $B$ denote IT2FSs. By using Zadeh’s extension principle, we define an IT2FS for a set of all real numbers $A\oplus B$ with the following equation:

$$\begin{aligned} (A\oplus B)(z)=\mathop {\sup }\limits _{z=x+y} \min \left[ {A(x), B(y)} \right] \!, \end{aligned}$$

(38)

where sup is the supremum. Based on interval-valued arithmetic, standard arithmetic operations on trapezoidal-shaped fuzzy numbers can be extended to IT2TrFNs.

Definition 6.4

Let $A$ and $B$ be two nonnegative IT2TrFNs. $A=[(a_1^L, a_2^L, a_3^L, a_4^L ;h_A^L ), (a_1^U, a_2^U, a_3^U, a_4^U ;h_A^U)]$, and $B=[(b_1^L, b_2^L , b_3^L, b_4^L ;h_B^L), (b_1^U, b_2^U, b_3^U, b_4^U ;h_B^U)]$ on $X$. The arithmetic operations on $A$ and $B$ are defined as follows:

$$\begin{aligned}&\begin{array}{l} A\oplus B=\left[ {\Big ({a_1^L +b_1^L, a_2^L +b_2^L, a_3^L +b_3^L, a_4^L +b_4^L ; }} \right. \\ \qquad {\min \{ {h_A^L, h_B^L } \}\Big ),\Big ({a_1^U \!+\!b_1^U, a_2^U \!+\!b_2^U, a_3^U \!+\!b_3^U, a_4^U \!+\!b_4^U}};\\ \qquad \left. {{\min \{ {h_A^U, h_B^U } \}}\Big )} \right] ; \\ \end{array}\end{aligned}$$

(39)

$$\begin{aligned}&\begin{array}{l} A\Theta B=\left[ {\Big ({a_1^L -b_4^L, a_2^L -b_3^L, a_3^L -b_2^L, a_4^L -b_1^L ; }} \right. \\ \qquad {\min \{ {h_A^L, h_B^L }\}\Big ),\Big ({a_1^U \!-\!b_4^U, a_2^U \!-\!b_3^U, a_3^U \!-\!b_2^U, a_4^U -b_1^U;}}\\ \qquad \left. {{\min \{ {h_A^U, h_B^U } \}}\Big )} \right] ; \\ \end{array}\end{aligned}$$

(40)

$$\begin{aligned}&\begin{array}{l} A\otimes B\!=\!\left[ {\Big ({a_1^L \cdot b_1^L, a_2^L \cdot b_2^L, a_3^L \cdot b_3^L, a_4^L \cdot b_4^L ;\min \{ {h_A^L, h_B^L }\}}\Big ), } \right. \\ \left. {\Big ({a_1^U \cdot b_1^U, a_2^U \cdot b_2^U, a_3^U \cdot b_3^U , a_4^U \cdot b_4^U ;\min \{ {h_A^U, h_B^U }\}}\Big )} \right] ; \\ \end{array} \end{aligned}$$

(41)

$$\begin{aligned}&\begin{array}{l} A\emptyset B=\left[ {\Big ({{a_1^L } / {b_4^L }, {a_2^L } /{b_3^L }, {a_3^L } / {b_2^L }, {a_4^L } / {b_1^L };\min \Big ({h_A^L, h_B^L }\Big )}\Big ), } \right. \\ \Big ({{a_1^U } / {b_4^U }, {a_2^U } / {b_3^U }, {a_3^U } / {b_2^U }, } \left. { {{a_4^U } / {b_1^U };\min \Big ({h_A^U, h_B^U }\Big )}\Big )} \right] , b_1^L, b_2^L,\\ b_3^L, b_4^L, b_1^U, b_2^U, b_3^U, b_4^U \ne 0; \\ \end{array}\nonumber \\ \end{aligned}$$

(42)

$$\begin{aligned}&\begin{array}{l} q\cdot A=A\cdot q \\ \quad =\left\{ \begin{array}{ll} \left[ {\Big (q\cdot a_1^L, q\cdot a_2^L, q\cdot a_3^L, q\cdot a_4^L ;h_A^L \Big ),}\right. &{}\quad {\hbox {if }q\ge 0, }\\ \left. { \Big (q\cdot a_1^U, q\cdot a_2^U, q\cdot a_3^U, q\cdot a_4^U ;h_A^U\Big )}\right] &{} \\ \left[ {\Big (q\cdot a_4^L, q\cdot a_3^L, q\cdot a_2^L, q\cdot a_1^L ;h_A^L\Big ),} \right] &{}\quad {\hbox {if }q\le 0;} \\ \left. {\Big (q\cdot a_4^U, q\cdot a_3^U, q\cdot a_2^U, q\cdot a_1^U ;h_A^U\Big )} \right] &{}\\ \end{array} \right. \\ \end{array}\nonumber \\ \end{aligned}$$

(43)

$$\begin{aligned}&A/q=\left\{ {{\begin{array}{ll} {\left[ {\left( {\frac{a_1^L }{q}, \frac{a_2^L }{q}, \frac{a_3^L }{q}, \frac{a_4^L }{q};h_A^L }\right) , \left( {\frac{a_1^U }{q}, \frac{a_2^U }{q}, \frac{a_3^U }{q}, \frac{a_4^U }{q};h_A^U }\right) } \right] } &{} {\hbox {if }q>0, } \\ {\left[ {\left( {\frac{a_4^L }{q}, \frac{a_3^L }{q}, \frac{a_2^L }{q}, \frac{a_1^L }{q};h_A^L }\right) , \left( {\frac{a_4^U }{q}, \frac{a_3^U }{q}, \frac{a_2^U }{q}, \frac{a_1^U }{q};h_A^U }\right) } \right] } &{} {\hbox {if }q<0.} \\ \end{array} }} \right. \nonumber \\ \end{aligned}$$

(44)

The multiplication and division operations produce approximate IT2TrFNs for simple computations.