Abstract
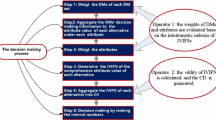
In the complex multi-attribute large-group decision making (CMALGDM) problems where attribute values are interval-valued intuitionistic fuzzy numbers (IVIFNs), the number of decision attributes is often large and their correlation degrees are high, which increase the difficulty of decision making and thus influence the accuracy of the result. To solve this problem, this paper proposes the interval-valued intuitionistic fuzzy principal component analysis (IVIF-PCA) model. This model represents major information of original attributes, effectively reduces dimensions of attribute space, and synthesizes original attributes into several relatively independent principal components (PCs). The basic thought of this model is as follows: first, we use thoughts of ‘equivalency’ and ‘order invariance’ to transform IVIFN samples into interval number samples; subsequently, we use the ‘error theory’ to replace interval numbers with their middle points, and combine the middle points with the traditional PCA to obtain the PC scores of interval number samples; finally, we adopt the thought of ‘equivalency’ to obtain the PC scores of IVIFN samples. Moreover, based on the IVIF-PCA model, we give a decision making method for the CMALGDM problem. The feasibility and validity of the decision making method is investigated through a numerical example.


Similar content being viewed by others
Explore related subjects
Discover the latest articles, news and stories from top researchers in related subjects.References
Atanassov KT (1986) Intuitionistic fuzzy sets. Fuzzy Sets Syst 20:87–96
Atanassov KT, Gargov G (1989) Interval-valued intuitionistic fuzzy sets. Fuzzy Sets Syst 31:343–349
Cazes P, Chouakria A, Diday E, Schektman Y (1997) Extension de l’analyse en composantes principales à des données de type intervalle. Revuede Statistique Appliquée 45:5–24
Chen XH (2009) Complex large-group decision making methods and application. Science Press, Beijing (in Chinese)
Chen TY, Li CH (2010) Determining objective weights with intuitionistic fuzzy entropy measures: a comparative analysis. Inf Sci 180:4207–4222
Chen Q, Xu ZS, Liu SS, Yu XH (2010) A method based on interval-valued intuitionistic fuzzy entropy for multiple attribute decision making. Inf Tokyo 13:67–77
Chen ZP, Yang W (2011) Appl Math Model 35:4424–4437
Douzal-Chouakria A, Billard L, Diday E (2011) Principal component analysis for interval-valued observations. Stat Anal Data Min 4:229–246
Guo JP, Li WH (2007) Principal component analysis based on error theory and its application. Appl Stat Manag 26:636–640 (in Chinese)
Herrera F, Herrera-Viedma E, Martínez L (2008) A fuzzy linguistic methodology to deal with unbalanced linguistic term sets. IEEE Trans Fuzzy Syst 16:354–370
Jolliffe I (2002) Principal component analysis. Springer, New York
Khaleie S, Fasanghari M (2012) An intuitionistic fuzzy group decision making method using entropy and association coefficient. Soft Comput 16:1197–1211
Kim SH, Choi SH, Kim JK (1999) An interactive procedure for multiple attribute group decision making with incomplete information: Range-based approach. Eur J Oper Res 118:139–152
Lauro NC, Palumbo F (2000) Principal components analysis of interval data: a symbolic data analysis approach. Computation Stat 15:73–87
Li DF (2010a) TOPSIS-based nonlinear-programming methodology for multiattribute decision making with interval-valued intuitionistic fuzzy sets. IEEE Trans Fuzzy Syst 18:299–311
Li DF (2010b) Linear programming method for MADM with interval-valued intuitionistic fuzzy sets. Expert Syst Appl 37:5939–5945
Liu BS et al. (2013) A partial binary tree DEA-DA cyclic classification model for decision makers in complex multi-attribute large-group interval-valued intuitionistic fuzzy decision-making problems. Inform Fusion. http://dx.doi.org/10.1016/j.inffus.2013.06.004
Merigó JM (2011) A unified model between the weighted average and the induced OWA operator. Expert Syst Appl 38:11560–11572
Merigó JM, Lobato-Carral C, Carrilero-Castillo A (2012) Decision making in the European Union under risk and uncertainty. Eur J Int Manag 6:590–609
Moore RE (1966) Interval Analysis. Prentice-Hall, Englewood Cliffs
Nayagam VLG, Muralikrishnan S, Sivaraman G (2011) Multicriteria decision-making method based on interval-valued intuitionistic fuzzy sets. Expert Syst Appl 38:1464–1467
Palumbo F, Lauro NC (2003) A PCA for interval-valued data based on midpoints and radii. In: Yanai H, Okada A, Shigemasu K, Kano Y, Meulman J (eds) New developments in psychometrics. Springer, Tokyo, pp 641–648
Tan CQ, Chen XH (2010) Intuitionistic fuzzy Choquet integral operator for multi-criteria decision making. Expert Syst Appl 37:149–157
Wang ZJ, Li KV, Wang WZ (2009) An approach to multiattribute decision making with interval-valued intuitionistic fuzzy assessments and incomplete weights. Inf Sci 179:3026–3040
Wei GW, Merigó JM (2012) Methods for strategic decision making problems with immediate probabilities in intuitionistic fuzzy setting. Sci Iran E 19:1936–1946
Xia MM, Xu ZS (2010) Generalized point operators for aggregating intuitionistic fuzzy information. Int J Intell Syst 25:1061–1080
Xu XH, Chen XH, Wang HW (2009) A kind of large group decision making method oriented utility valued preference information. Control Decis 24:440–446 (in Chinese)
Xu XH, Yong YF (2011) Improved ants-clustering algorithm and its application in multi-attribute large group decision making. J Syst Eng Electron 33:346–349 (in Chinese)
Xu ZS (2007a) Intuitionistic fuzzy aggregation operators. IEEE Trans Fuzzy Syst 15:1179–1187
Xu ZS (2007b) A method for multiple attribute decision making with incomplete weight information in linguistic setting. Knowl Based Syst 20:719–725
Xu ZS (2007c) Models for multiple attribute decision making with intuitionistic fuzzy information. Int J Uncertain Fuzz 15:285–297
Xu ZS (2007d) Methods for aggregating interval-valued intuitionistic fuzzy information and their application to decision making. Control Decis 22:215–219 (in Chinese)
Xu ZS (2010a) A deviation-based approach to intuitionistic fuzzy multiple attribute group decision making. Group Decis Negotiat 19:57–76
Xu ZS (2010b) A method based on distance measure for interval-valued intuitionistic fuzzy group decision making. Inf Sci 180:181–190
Xu ZS, Yager RR (2006) Some geometric aggregation operators based on intuitionistic fuzzy sets. Int J Gen Syst 35:417–433
Zadeh LA (1965) Fuzzy sets. Inf Control 8:338–353
Acknowledgments
We would like to thank the two anonymous reviewers for their constructive comments that have helped to improve the presentation and quality of the paper. This paper was supported by the National Natural Science Foundation of China (No. 71102072, No. 71271143, No. 71171141, and No. 71171202).
Author information
Authors and Affiliations
Corresponding author
Additional information
Communicated by Z. Zhu.
Electronic supplementary material
Below is the link to the electronic supplementary material.
Rights and permissions
About this article
Cite this article
Liu, B., Chen, Y., Shen, Y. et al. A complex multi-attribute large-group decision making method based on the interval-valued intuitionistic fuzzy principal component analysis model. Soft Comput 18, 2149–2160 (2014). https://doi.org/10.1007/s00500-013-1190-8
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00500-013-1190-8