Abstract
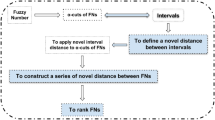
Recently, Guha and Chakraborty studied a new approach to fuzzy distance measure and similarity measure between two generalized fuzzy numbers. In this paper, we propose a family of fuzzy distance measures between arbitrary fuzzy numbers depending on a defuzzification, an interval similarity measure, and some real pseudosemimetrics, involving some of the most important possibilistic and geometric characteristics of any fuzzy number. Then, we study its metric properties and its relationship with a partial order on the set of all trapezoidal fuzzy numbers. Illustrative examples about the action of this class of metrics are shown, comparing them with the results obtained by other researchers. Finally, as application, we introduce a fuzzy ranking and we compare it with other techniques.



Similar content being viewed by others
Explore related subjects
Discover the latest articles, news and stories from top researchers in related subjects.Notes
We use the term radius in the sense that if \(c\) is the center and \(r\) is the radius, then the interval is \(\left[ c-r,c+r\right] \).
References
Adabitabar Firozja M, Fath-Tabar GH, Eslampia Z (2012) The similarity measure of generalized fuzzy numbers based in interval distance. Appl Math Lett 25:1528–1534
Allahviranloo T, Firozja MA (2010) Ranking of fuzzy numbers by a new metric. Soft Comput 14:773–783
Allahviranloo T, Nuraei R, Ghanbari M, Haghi E, Hossein-zadeh AA (2012) A new metric for \(L\)-\(R\) fuzzy numbers and its application in fuzzy linear systems. Soft Comput 16:1743–1754
Ban AI, Coroianu L (2012) Nearest interval, triangular and trapezoidal approximation of a fuzzy number preserving ambiguity. Int J Approx Reas 53:805–836
Buckley JJ, Jowers LJ (2008) Monte Carlo methods in fuzzy optimization. In: Studies in fuzziness and soft computing, vol 222. Springer, Berlin
Chang CT (2010) An approximation approach for representing S-shaped membership functions. IEEE Trans Fuzzy Syst 18(2):412–424 (2010), art. no. 5411779
Chen SM (1996) New methods for subjective mental workload assessment and fuzzy risk analysis. Cybern Syst 27:449–472
Chen SJ, Chen SM (2003) Fuzzy risk analysis based on similarity measures of generalized fuzzy numbers. IEEE Trans Fuzzy Syst 11:45–56
Cheng CH (1988) A new approach for ranking fuzzy numbers by distance method. Fuzzy Sets Syst 95:307–317
Dubois D, Prade H (1978) Operations on fuzzy numbers. Int J Syst Sci 9:613–626
Dubois D, Prade H (1988) Possibility theory. Plenum Press, New York
Dubois D, Prade H (2005) Fuzzy elements in a fuzzy set. In: Proceedings of the 10th International Fuzzy Systems Association (IFSA) Congress. Springer, Beijing, pp 55–60
Ganesan T, Vasant P, Elamvazuthi I (2012) Hybrid PSO approach for solving non-convex optimization problems. Arch Control Sci 22(1):5–23
Goetschel R, Voxman W (1986) Elementary fuzzy calculus. Fuzzy Sets Syst 18:31–43
Guha D, Chakraborty D (2010) A new approach to fuzzy distance measure and similarity measure between two generalized fuzzy numbers. Appl Soft Comput 10:90–99
Lee HS (1999) An optimal aggregation method for fuzzy opinions of group decision. Proc IEEE Int Conf Syst Man Cybern 3:314–319
Mizumoto M, Tanaka J (1979) Some properties of fuzzy numbers. In: Gupta MM et al (eds) Advances in fuzzy set theory and applications. North-Holland, New York, pp 153–164
Nejad AM, Mashinchi M (2011) Ranking fuzzy numbers based on the areas on the left and the right sides of fuzzy number. Comput Math Appl 61:431–442
Peidro D, Vasant P (2011) Transportation planning with modified s-curve membership functions using an interactive fuzzy multi-objective approach. Appl Soft Comput 11:2656–2663
Rodabaugh SE (1999a) Categorical foundations of variable-basis fuzzy topology, mathematics of fuzzy sets: logic, topology and measure theory. In: Höhle U, Rodabaugh SE (eds) The handbooks of fuzzy sets series, vol 3. Kluwer Academic Publishers, Dordrecht, pp 273–388
Rodabaugh SE (1999b) Fuzzy real lines and dual real lines as poslat topological, uniform, and metric ordered semirings with unity, mathematics of fuzzy sets: logic, topology and measure theory. In: Höhle U, Rodabaugh SE (eds) The handbooks of fuzzy sets series, vol 3. Kluwer Academic Publishers, Dordrecht, pp 607–631
Roldán A, Martínez-Moreno J, Roldán C (2012) A fuzzy regression model based on distances and random variables with crisp input and fuzzy output data: a case study in biomass production. Soft Comput 16:785–795
Roldán A, Martínez-Moreno J, Roldán C (2014) Some applications of the study of the image of a fuzzy number: countable fuzzy numbers, operations, regression and a specificity-type ordering, Fuzzy Sets Syst 257:204–216. doi:10.1016/j.fss.2013.07.003
Schweizer B, Sklar A (2005) Probabilistic metric spaces. Dover Publications, New York
Tran L, Duckstein L (2002) Comparison of fuzzy numbers using a fuzzy distance measure. Fuzzy Sets Syst 130:331–341
Vasant P, Barsoum N (2010) Hybrid pattern search and simulated annealing for fuzzy production planning problems. Comput Math Appl 60(4):1058–1067
Vasant PM (2013) Meta-heuristics optimization algorithms in engineering, business, economics, and finance. IGI Global, Hershey, PA, pp 1–734
Vasant P, Ganesan T, Elamvazuthi I (2012) Hybrid tabu search Hopfield recurrent ANN fuzzy technique to the production planning problems: a case study of crude oil in refinery industry. Int J Manuf Mater Mech Eng 2(1):47–65
VicenteRiera J, Torrens J (2012) Aggregation of subjective evaluations based on discrete fuzzy numbers. Fuzzy Sets Syst 191:21–40
Voxman W (2001) Canonical representations of discrete fuzzy numbers. Fuzzy Sets Syst 118:457–466
Wu CX, Ma M (1991) The basic of fuzzy analysis. National Defence Industry Press, Beijing
Acknowledgments
We are very thankful to the anonymous reviewers for their careful reading of our manuscript and for their constructive reports, which have been very useful to improve the paper.
Author information
Authors and Affiliations
Corresponding author
Additional information
Communicated by V. Loia.
Appendix A: Proofs
Appendix A: Proofs
For the sake of completeness, we include here the proofs of lemmas we have announced throughout the paper.
Proof
(Lemma 2.5, page 4) It is clear that:
Similarly,
As \(\mathcal {D}_{c}\mathcal {A}=(1/2)\underline{a}_{1}+(1/2)\overline{a}_{1}\) for all \(\mathcal {A}\in \mathcal {F}\) (that is, \(n=1\) and \(\beta _{1}=\gamma _{1}=1/2\)), the same properties hold for \(\mathcal {D}_{c}\). \(\square \)
Proof
(Lemma 2.6, page 4) (1) By definition,
(2) Similarly,
(3) Similarly,
\(\square \)
Proof
(Example 3.3, page 5) It is clear that \(\phi (x,y)=0\) iff \(x=y\) and \(\phi (x,y)=\phi (y,x)\). If \(p=1\), then \(q\left| x-z\right| \le q\left| x-y\right| +q\left| y-z\right| \). Suppose that \(0<p<1\) and we claim that
Fix \(x,z\in \mathbb {R}\). If \(x=z\), then (8) is trivial. Suppose that \(x<z\) without lost of generality. Consider the mapping \(h(y)=\left| x-y\right| ^{p}+\left| y-z\right| ^{p}-\left| x-z\right| ^{p}\) for all \(y\in \mathbb {R}\). Clearly, \(h\) is continuous on \(\mathbb {R}\) and \(h(x)=h(z)=0\). Let \(a=\left( z-x\right) ^{p}\). Then, we can decompose:
It is not difficult to prove that \(h^{\prime }(y)<0\) for all \(y<x\) and \(h^{\prime }(y)>0\) for all \(y>z\). Therefore, \(h\) is strictly decreasing on \(\left] -\infty ,x\right[ \) and strictly increasing on \(\left] z,\infty \right[ \). Therefore, \(h\) has al least one absolute minimum, which is on \(\left[ x,z\right] \). As \(h^{\prime \prime }(y)<0\) for all \(y\in \left] x,z\right[ \), its minimum is not in \(\left] x,z\right[ \), but in \(\left\{ x,z\right\} \). As \(h(x)=h(z)=0\), then \(h(y)\ge 0\) for all \(y\in \mathbb {R}\), so (8) is true. \(\square \)
Proof
(Lemma 3.6, page 6) Suppose that \(I=[a,b]\), \(I^{\prime }=[a^{\prime },b^{\prime }]\), \(J=[c,e]\), \(J^{\prime }=[c^{\prime },e^{\prime }]\) and \(K=[f,g]\).
(1) As \(\underline{\delta }(I,J)=-\left| a-c\right| \le 0\) and \(\overline{\delta }(I,J)=\left| b-e\right| \ge 0\), then \(0_{\mathcal {I}}=[0,0]\subseteq \delta (I,J)\). Therefore, \(\delta (I,J)\in \mathcal {I}_{0_{\mathcal {I}},\subseteq }^{+}\). It is clear that:
Moreover, \(\delta \) is symmetric. Finally, as \(\left| a-f\right| \le \left| a-c\right| +\left| c-f\right| \) (so \(-\left| a-f\right| \ge -\left| a-c\right| -\left| c-f\right| \)) and \(\left| b-g\right| \le \left| b-e\right| +\left| e-g\right| \)
(2) If \(I\subseteq I^{\prime }\) and \(J\subseteq J^{\prime }\), then \(a^{\prime }\le a\le b\le b^{\prime }\) and \(c^{\prime }\le c\le e\le e^{\prime }\). Then, \(a^{\prime }+c^{\prime }\le a+c\le b+e\le b^{\prime }+e^{\prime }\), so
(3)
(4) If \(I\subseteq J\cap K\), then \(c\le a\le b\le e\) and \(f\le a\le b\le g\). Then, \([c-a,e-b]=\delta (I,J)=\delta (I,K)=[f-a,g-b]\), so \(J=[c,e]=[f,g]=K\).
(5) If \(I\subseteq J\), then \(c\le a\le b\le e\). Therefore, then \(c+f\le a+f\le b+f\le b+g\le e+g\), so then \(I+K=[a+f,b+g]\subseteq [c+f,e+g]=J+K\). \(\square \)
Proof
(Lemma 4.8, page 10) Since \(\phi _{1}\), \(\phi _{3}\), \(\phi _{4}\) and \(\psi _{2}\) are pseudosemimetrics, then
for all \(\phi \in \{\phi _{1},\phi _{3},\phi _{4},\psi _{2}\}\) and all \(\mathcal {A},\mathcal {B}\in \mathcal {F}\). As a consequence, for all \(\alpha \in \mathbb {I}\),
and similarly \(\overline{D(\mathcal {A},\mathcal {A})}_{\alpha }=0\). Therefore, \(D(\mathcal {A},\mathcal {A})=\tilde{0}\). Furthermore, as \(\delta \) is also symmetric,
and similarly \(\overline{D(\mathcal {B},\mathcal {A})}_{\alpha }=\overline{D(\mathcal {A},\mathcal {B})}_{\alpha }\) for all \(\alpha \in \mathbb {I}\). Hence, \(D(\mathcal {B},\mathcal {A})=D(\mathcal {A},\mathcal {B})\).
Proof
(Lemma 4.10, page 10) (1) As \(h_{1}(1)=h_{2}(1)=0\), it is clear that:
(2) From (1):
(3) Similarly:
(4) If \(\mathcal {D}=\mathcal {D}_{c}\), then item 2 shows us that \(\mathcal {D}_{c}(D(\mathcal {A} ,\mathcal {B}))=q_{1}\phi _{1}(\mathcal {DA},\mathcal {DB})\ge 0\). Hence, by item 3 of Lemma 4.2, \(D(\mathcal {A} ,\mathcal {B})\succcurlyeq \tilde{0}\) w.r.t. \((\mathcal {D}_{c},\delta ,\subseteq )\). \(\square \)
Proof
(Statement before Theorem 4.13) Suppose that \(\mathcal {A}=(a/b/c/e)\) and \(\mathcal {B}=(a^{\prime }/b^{\prime }/c^{\prime }/e^{\prime })\). If \(D(\mathcal {A} ,\mathcal {B})\) is a crisp FN, then
This means that \(\hbox {spr}\mathcal {A}=\hbox {spr} \mathcal {B}\) and \(\delta (\ker \mathcal {A},\hbox {supp}\mathcal {A} )=\delta (\ker \mathcal {B},\hbox {supp}\mathcal {B})\), i.e.,
If \(r=a-a^{\prime }\), then \(b-b^{\prime }=c-c^{\prime }=e-e^{\prime }=r\), so \(a=r+a^{\prime }\), \(b=r+b^{\prime }\), \(c=r+c^{\prime }\) and \(e=r+e^{\prime }\). \(\square \)
Proof
(Theorem 4.13, page 12) Firstly, we are going to characterize:
Indeed, let \(\mathcal {B}\in N_{r}(\mathcal {A})\). As \(D(\mathcal {A} ,\mathcal {B})\prec \tilde{r}\), then
As \(D(\mathcal {A},\mathcal {B})\) is rectangular but \(\hbox {spr} D(\mathcal {A},\mathcal {B})=0\), then \(D(\mathcal {A},\mathcal {B})\) is a crisp FN. In this case, we have just proved that \(\mathcal {B}\) is a translation of \(\mathcal {A}\), i.e., there exists \(s\in \mathbb {R}\) such that \(\mathcal {B} =s+\mathcal {A}\). Taking defuzzification, \(\mathcal {D}_{c}\mathcal {B} =\mathcal {D}_{c}(s+\mathcal {A})=\mathcal {D}_{c}s+\mathcal {D}_{c} \mathcal {A}=s+\mathcal {D}_{c}\mathcal {A}\), so \(s=\mathcal {D}_{c} \mathcal {B}-\mathcal {D}_{c}\mathcal {A}\). If \(q_{1}\phi _{1}(\mathcal {D} _{c}\mathcal {A},\mathcal {D}_{c}\mathcal {B})=r\), then \(D(\mathcal {A} ,\mathcal {B})\preccurlyeq \tilde{r}\) and \(\tilde{r}\preccurlyeq D(\mathcal {A} ,\mathcal {B})\), so \(D(\mathcal {A},\mathcal {B})=\tilde{r}\), but we suppose that \(D(\mathcal {A},\mathcal {B})\prec \tilde{r}\). Then, \(q_{1}\phi _{1} (\mathcal {D}_{c}\mathcal {A},\mathcal {D}_{c}\mathcal {B})<r\).
Next, we are going to see that \(\beta _{\mathcal {A}}=\{N_{r}(\mathcal {A} )\}_{r>0}\) is a neighborhood system at \(\mathcal {A}\). We have to prove three properties.
First two properties are trivial, since \(\mathcal {A}\in N_{r}(\mathcal {A})\) for all \(r>0\) and \(N_{r_{3}}(\mathcal {A})\subseteq N_{r_{1}}(\mathcal {A})\cap N_{r_{2}}(\mathcal {A})\) if \(0<r_{3}<\min (r_{1},r_{2})\). Let \(U=U_{0} =N_{r}(\mathcal {A})\) and let \(\mathcal {B}\in N_{r}(\mathcal {A})\). If \(\mathcal {B}=\mathcal {A}\), we can take \(V=U\). Suppose that \(\mathcal {B} \ne \mathcal {A}\). As \(q_{1}\phi _{1}(\mathcal {D}_{c}\mathcal {A},\mathcal {D} _{c}\mathcal {B})<r\), let \(s,\varepsilon >0\) such that \(q_{1}\phi _{1} (\mathcal {D}_{c}\mathcal {A},\mathcal {D}_{c}\mathcal {B})<s<s+\varepsilon <r\). Consider \(V=N_{\varepsilon }(\mathcal {B})\in \beta _{\mathcal {B}}\) and we have to prove that \(N_{\varepsilon }(\mathcal {B})\subseteq N_{r}(\mathcal {A})\). Indeed, let \(\mathcal {C}\in N_{\varepsilon }(\mathcal {B})\). We know that \(\mathcal {C} =(\mathcal {D}_{c}\mathcal {C}-\mathcal {D}_{c}\mathcal {B})+\mathcal {B}\) and \(q_{1}\phi _{1}(\mathcal {D}_{c}\mathcal {B},\mathcal {D}_{c}\mathcal {C} )<\varepsilon \). Then:
On the other hand,
where we have used properties like the following
(that are easy to prove in general). Therefore, \(\mathcal {C}\in N_{r} (\mathcal {A})\) and we have proved that \(N_{\varepsilon }(\mathcal {B})\subseteq N_{r}(\mathcal {A})\). General Topology guarantees that there exists an unique topology on \(\mathcal {T}\) such that \(\beta _{\mathcal {A}}=\{N_{1/n} (\mathcal {A})\}_{n\in \mathbb {N}}\) is a (countable) neighborhood system at \(\mathcal {A}\). We only have to prove that it is Hausdorff.
Let \(\mathcal {A},\mathcal {B}\in \mathcal {T}\) such that \(\mathcal {A} \ne \mathcal {B}\). We distinguish two cases. Firstly, suppose that \(\mathcal {D}_{c}\mathcal {A}\ne \mathcal {D}_{c}\mathcal {B}\) and let \(r=q_{1}\phi _{1}(\mathcal {D}_{c}\mathcal {A},\mathcal {D}_{c}\mathcal {B})/4>0\). To see that \(N_{r}(\mathcal {A})\cap N_{r}(\mathcal {B})=\varnothing \), suppose that \(\mathcal {C}\in N_{r}(\mathcal {A})\cap N_{r}(\mathcal {B})\). In this case,
but this is impossible. Therefore, \(N_{r}(\mathcal {A})\cap N_{r} (\mathcal {B})=\varnothing \).
Now suppose that \(\mathcal {D}_{c}\mathcal {A}=\mathcal {D}_{c}\mathcal {B}\). As \(\mathcal {C}\in N_{r}(\mathcal {A})\cap N_{r}(\mathcal {B})\), then \(\mathcal {C}=(\mathcal {D}_{c}\mathcal {C}-\mathcal {D}_{c}\mathcal {A} )+\mathcal {A}\) and \(\mathcal {C}=(\mathcal {D}_{c}\mathcal {C}-\mathcal {D} _{c}\mathcal {B})+\mathcal {B}\). Therefore, we can prove that \(\mathcal {A} =(\mathcal {D}_{c}\mathcal {A}-\mathcal {D}_{c}\mathcal {C})+\mathcal {C}\) and \(\mathcal {B}=(\mathcal {D}_{c}\mathcal {B}-\mathcal {D}_{c}\mathcal {C} )+\mathcal {C}\) (it is not difficult to prove that if \(\mathcal {A} =s+\mathcal {B}\), then \(\mathcal {B}=(-s)+\mathcal {A}\)). Since \(\mathcal {D} _{c}\mathcal {A}=\mathcal {D}_{c}\mathcal {B}\), it follows that \(\mathcal {A} =\mathcal {B}\), but this is impossible. Therefore, \(N_{r}(\mathcal {A})\cap N_{r}(\mathcal {B})=\varnothing \) in any case and the topology is Hausdorff. \(\square \)
Rights and permissions
About this article
Cite this article
Aguilar-Peña, C., Roldán-López de Hierro, AF., Roldán-López de Hierro, C. et al. A family of fuzzy distance measures of fuzzy numbers. Soft Comput 20, 237–250 (2016). https://doi.org/10.1007/s00500-014-1497-0
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00500-014-1497-0