Abstract
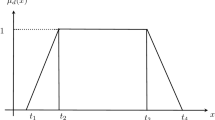
This paper analyzes the pricing decisions of a dual-channel supply chain including one retailer and one manufacturer who produces a product and sells it to the end customer through retailer or directly. Both the manufacturing cost and the customer demand are considered as fuzzy variables. Two pricing models, including centralized decision model and manufacturer-leader Stackelberg game, with consideration of different market power structures are adopted. Optimal decisions on wholesale price and retail prices are determined using game theoretical approach and fuzzy set theory for each model. Finally, a numerical example is solved to illustrate the effectiveness of models and provide some managerial insights from analysis.
Similar content being viewed by others
Explore related subjects
Discover the latest articles, news and stories from top researchers in related subjects.References
Cao P, Li J, Yan H (2012) Optimal dynamic pricing of inventories with stochastic demand and discounted criterion. Eur J Oper Res 217(3):580–588
Chen CY, Fang S, Wen U (2013) Pricing policies for substitutable products in a supply chain with Internet and traditional channels. Eur J Oper Res 224(3):542–551
Karakul M, Chan LMA (2010) Joint pricing and procurement of substitutable products with random demands—a technical note. Eur J Oper Res 201(1):324–328
Liu B (2002) Theory and practice of uncertain programming. Physica-Verlag, Heidelberg
Liu B, Liu Y (2002) Excepted value of fuzzy variable and fuzzy expected value models. IEEE Trans Fuzzy Syst 10(4):445–450
Liu B (2004) Uncertainty theory: an introduction to its axiomatic foundation. Springer, Berlin
Liu Y, Liu B (2003) Expected value operator of random fuzzy variable and random fuzzy expected value models. Int J Uncertain Fuzziness Knowl-Based Syst 11(2):195–215
McGuire TW, Staelin R (1983) An industry equilibrium analyses of down stream vertical integration. Mark Sci 2:161–191
Nahmias S (1978) Fuzzy variables. Fuzzy Sets Syst 1(2):97–110
Wang C, Tang W, Zhao R (2007) On the continuity and convexity analysis of the expected value function of a fuzzy mapping. J Uncertain Syst 1(2):148–160
Wei J, Zhao J (2011) Pricing decisions with retail competition in a fuzzy closed-loop supply chain. Expert Syst Appl 38(9):1209–11216
Wei J, Zhao J (2013) Reverse channel decisions for a fuzzy closed-loop supply chain. Appl Math Model 37(3):1502–1513
Wei J, Zhao J, Li Y (2013) Pricing decisions for complementary products with firms’ different market powers. Eur J Oper Res 224(3):507–519
Wei J, Zhao J (2014) Pricing decisions for substitutable products with horizontal and vertical competition in fuzzy environments. Ann Oper Res. doi:10.1007/s10479-014-1541-6
Xie Y, Petrovic D, Burnham K (2006) A heuristic procedure for the two-level control of serial supply chains under fuzzy customer demand. Int J Prod Econ 102:37–50
Zadeh L (1965) Fuzzy sets. Inf Control 8(3):338–353
Zhang R, Liu B, Wang W (2012) Pricing decisions in a dual channels system with different power structures. Econ Model 29(2):523–533
Zhao J, Tang W, Wei J (2012) Pricing decision for substitutable products with retail competition in a fuzzy environment. Int J Prod Econ 135(1):144–153
Zhao J, Tang W, Zhao R, Wei J (2012) Pricing decisions for substitutable products with a common retailer in fuzzy environments. Eur J Oper Res 216(2):409–419
Zimmermann HJ (2000) Application-oriented view of modeling uncertainty. Eur J Oper Res 122(2):190–198
Author information
Authors and Affiliations
Corresponding author
Additional information
Communicated by V. Loia.
Rights and permissions
About this article
Cite this article
Soleimani, F. Optimal pricing decisions in a fuzzy dual-channel supply chain. Soft Comput 20, 689–696 (2016). https://doi.org/10.1007/s00500-014-1532-1
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00500-014-1532-1