Abstract
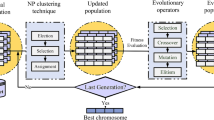
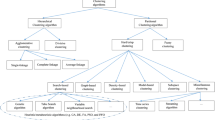
Clustering algorithms, a fundamental base for data mining procedures and learning techniques, suffer from the lack of efficient methods for determining the optimal number of clusters to be found in an arbitrary dataset. The few methods existing in the literature always use some sort of evolutionary algorithm having a cluster validation index as its objective function. In this article, a new evolutionary algorithm, based on a hybrid model of global and local heuristic search, is proposed for the same task, and some experimentation is done with different datasets and indexes. Due to its design, independent of any clustering procedure, it is applicable to virtually any clustering method like the widely used \(k\)-means algorithm. Moreover, the use of non-parametric statistical tests over the experimental results, clearly show the proposed algorithm to be more efficient than other evolutionary algorithms currently used for the same task.











Similar content being viewed by others
Explore related subjects
Discover the latest articles, news and stories from top researchers in related subjects.References
Arabas J, Michalewicz Z, Mulawka J (1994) GAVaPS-a genetic algorithm with varying population size. In: Proceedings of the first IEEE conference on evolutionary computation, IEEE world congress on computational intelligence. IEEE, pp 73–78
Bandyopadhyay S, Maulik U (2002) An evolutionary technique based on k-means algorithm for optimal clustering in rn. Inf Sci 146(1):221–237
Bandyopadhyay S, Maulik U (2002) Genetic clustering for automatic evolution of clusters and application to image classification. Pattern Recognit 35(6):1197–1208
Bellis MA, Jarman I, Downing J, Perkins C, Beynon C, Hughes K, Lisboa P (2012) Using clustering techniques to identify localities with multiple health and social needs. Health Place 18(2):138–143
Cao J, Wu Z, Wu J, Liu W (2012) Towards information-theoretic k-means clustering for image indexing. Signal Process 39(2):1–12
Chang L, Duarte MM, Sucar L, Morales EF (2012) A bayesian approach for object classification based on clusters of sift local features. Expert Syst Appl 39(2):1679–1686
Cortina-Borja M (2012) Handbook of parametric and nonparametric statistical procedures. J R Stat Soc: Ser A (Stat Soc) 175(3):829–829
Das S, Abraham A, Konar A (2008) Automatic clustering using an improved differential evolution algorithm. Syst Man Cybern Part A: Syst Hum IEEE Trans 38(1):218–237
Davies David L, Bouldin DW (1979) A cluster separation measure. IEEE Trans Pattern Anal Mach Intel 2:224–227
Franek L, Abdala D, Vega-Pons S, Jiang X (2011) Image segmentation fusion using general ensemble clustering methods. Comput Vis-ACCV 2010:373–384
Garcia S, Molina D, Lozano M, Herrera F (2009) A study on the use of non-parametric tests for analyzing the evolutionary algorithms? behaviour: a case study on the cec 2005 special session on real parameter optimization. J Heuristics 15(6):617–644
Gordon AD (1999) Classification. Chapman & Hall/CRC Monographs on Statistics & Applied Probability
Hong Y, Kwong S, Chang Y, Ren Q (2008) Unsupervised feature selection using clustering ensembles and population based incremental learning algorithm. Pattern Recognit 41(9):2742–2756
Jarboui B, Cheikh M, Siarry P, Rebai A (2007) Combinatorial particle swarm optimization (cpso) for partitional clustering problem. Appl Math Comput 192(2):337–345
Kanade PM, Hall LO (2003) Fuzzy ants as a clustering concept. In: Fuzzy Information Processing Society, 2003. NAFIPS 2003. 22nd International Conference of the North American, pp 227–232. IEEE
Kwedlo W (2011) A clustering method combining differential evolution with the \(k\)-means algorithm. Pattern Recognit Lett 32(12):1613–1621
Lee W-P, Chen SW (2010) Automatic clustering with differential evolution using a cluster number oscillation method. Intelligent Systems and Applications pp 218–237
Lu Y, Lu S, Fotouhi F, Deng Y, Brown SJ (2004) Fgka: a fast genetic k-means clustering algorithm. In: Proceedings of the 2004 ACM symposium on Applied computing, pp 622–623. ACM
Maulik U, Bandyopadhyay S (2002) Performance evaluation of some clustering algorithms and validity indices. IEEE Trans Pattern 24(12):1650–1654
Milligan GW, Cooper MC (1985) An examination of procedures for determining the number of clusters in a data set. Psychometrika 50:159–179
Omran M, Engelbrecht AP, Salman A (2005) Particle swarm optimization method for image clustering. Int J Pattern Recognit Artif Intel 19(03):297–321
Parsopoulos KE (2009) Cooperative micro-differential evolution for high-dimensional problems. In: Proceedings of the 11th Annual conference on Genetic and evolutionary computation, pp 531–538. ACM
Saha I, Maulik U, Bandyopadhyay S (2009) A new differential evolution based fuzzy clustering for automatic cluster evolution. Advance Computing Conference, 2009. IACC 2009. IEEE International pp 706–711
Storn R, Price K (1997) Differential evolution-a simple and efficient heuristic for global optimization over continuous spaces. J Global Optim 11(4):341–359
Sugar CA, James GM (2003) Finding the number of clusters in a dataset. J Am Stat Assoc 98(463):750–763
Villa A, Chanussot J, Benediktsson JA, Jutten C, Dambreville R (2012) Unsupervised methods for the classification of hyperspectral images with low spatial resolution. Pattern Recognit 46(6):1556–1568
Witt C (2008) Population size versus runtime of a simple evolutionary algorithm. Theor Comput Sci 403(1):104–120
Xie XL, Beni GA (1991) Validity measure for fuzzy clustering. IEEE Trans Pattern Anal Mach Intell 13(4):841–847
Yan H, Chen K, Liu L, Yi Z (2010) Scale: a scalable framework for efficiently clustering transactional data. Data Min Knowl Discov 20(1):1–27
Yang Y, Liao Y (2011) A hybrid feature selection scheme for unsupervised learning and its application in bearing fault diagnosis. Expert Syst Appl 38(9):1311–1320
Acknowledgments
Mexican authors wish to express their gratitude to SIP-IPN, CONACyT and ICyT-DF for their economic support of this research, particularly, through grants SIP-20130932 and ICyT-PICCO-10-113. Spanish Ministry & Economy competitiveness and FEDER contract roadMe (http://roadme.lcc.uma.es): Fundamentals for Real World Applications of Metaheuristics: The Vehicular Network Case TIN2011-28194 (2012–2014).
Author information
Authors and Affiliations
Corresponding author
Additional information
Communicated by V. Loia.
Rights and permissions
About this article
Cite this article
Arellano-Verdejo, J., Alba, E. & Godoy-Calderon, S. Efficiently finding the optimum number of clusters in a dataset with a new hybrid differential evolution algorithm: DELA. Soft Comput 20, 895–905 (2016). https://doi.org/10.1007/s00500-014-1548-6
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00500-014-1548-6