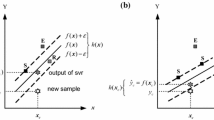
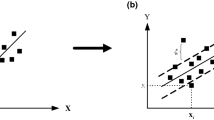
Abstract
In this study, a novel online support vector regressor (SVR) controller based on system model estimated by a separate online SVR is proposed. The main idea is to obtain an SVR controller based on an estimated model of the system by optimizing the margin between reference input and system output. For this purpose, “closed-loop margin” which depends on tracking error is defined, then the parameters of the SVR controller are optimized so as to optimize the closed-loop margin and minimize the tracking error. In order to construct the closed-loop margin, the model of the system estimated by an online SVR is utilized. The parameters of the SVR controller are adjusted via the SVR model of system. The stability of the closed-loop system has also been analyzed. The performance of the proposed method has been evaluated by simulations carried out on a continuously stirred tank reactor (CSTR) and a bioreactor, and the results show that SVR model and SVR controller attain good modeling and control performances.































Similar content being viewed by others
Explore related subjects
Discover the latest articles, news and stories from top researchers in related subjects.References
Astrom KJ, Wittenmark B (2008) Adaptive control. Dover Publications, Mineola
Butler H (1992) Model reference adaptive control: from theory to practice. Prentice Hall, Great Britain
Camacho EF (1993) Constrained generalized predictive control. IEEE Trans Autom Control 38(2):327–332. doi:10.1109/9.250485
Camacho EF, Bordons C (1999) Model predictive control. Springer, New York
Clarke DW, Mohtadi C (1989) Properties of generalized predictive control. Automatica 25(6):859–875. doi:10.1016/0005-1098(89)90053-8
Clarke DW, Mohtadi C, Tuffs P (1987) Generalized predictive control-part I: the basic algorithm. Automatica 23(2):137–148. doi:10.1016/0005-1098(87)90087-2
Cristianini N, Shawe-Taylor J (2000) An introduction to support vector machines and other kernel-based learning methods. Cambridge University Press, Cambridge
Efe MO (2007) Discrete time fuzzy sliding mode control of a biochemical process. In: Proceedings of 9th WSEAS international conference on automatic control, modeling and simulation (ACMOS’07), Istanbul
Fogler HH (2006) Elements of chemical reaction engineering. Pearson Education, USA
Han F, Wang Z, Lei M, Zhou Z (2008) An iterative modified kernel for support vector regression. In: Proceedings of IEEE international conference on cybernetic intelligent systems (CIS 2008), Chengdu
Haykin S (1999) Neural networks: a comprehensive foundation. Prentice Hall, New Jersey
Iplikci S (2006a) Online trained support vector machines-based generalized predictive control of non-linear systems. Int J Adapt Control Signal Process 20(10):599–621. doi:10.1002/acs.919
Iplikci S (2006b) Support vector machines-based generalized predictive control. Int J Robust Nonlinear Control 16(17):843–862. doi:10.1002/rnc.1094
Iplikci S (2010) A comparative study on a novel model-based PID tuning and control mechanism for nonlinear systems. Int J Robust Nonlinear Control 20(13):1483–1501. doi:10.1002/rnc.1524
Kravaris C, Palanki S (1988) Robust nonlinear state feedback under structured uncertainty. AIChe J 34(7):1119–1127. doi:10.1002/aic.690340708
Levenspiel O (1999) Chemical reaction engineering. Wiley, USA
Liu X, Yi J, Zhao D (2005) Adaptive inverse control system based on least squares support vector machines. In: Proceedings of 2nd international symposium on neural networks (ISNN 2005), Chongqing
Ma J, Theiler J, Perkins S (2003) Accurate online support vector regression. Neural Comput 15(11):2683–2703. doi:10.1162/089976603322385117
Mario M (2002) On-line support vector machine regression. In: Proceedings of 13th European conference on machine learning (ECML 2002), Helsinki
Norgaard M, Ravn O, Poulsen N, Hansen L (2000) Neural networks for modelling and control of dynamic systems. Springer, Great Britain
Saadia N, Amirat Y, Pontnau J, M’Sirdi NK (2001) Neural hybrid control of manipulators, stability analysis. Robotica 19:41–51. doi:10.1017/S0263574700002885
Shin J, Jin Kim H, Park S, Kim Y (2010) Model predictive flight control using adaptive support vector regression. Neurocomputing 73(4–6):1031–1037. doi:10.1016/j.neucom.2009.10.002
Smola AJ, Schlkopf B (2004) A tutorial on support vector regression. Stat Comput 14(3):199–222. doi:10.1023/B:STCO.0000035301.49549.88
Sun C, Song J (2007) An adaptive internal model control based on LS-SVM. In: Proceedings of 4th international symposium on neural networks (ISNN 2007), Nanjing
Takao K, Yamamoto T, Hinamoto T (2006) A design of PID controllers with a switching structure by a support vector machine. In: Proceedings of 2006 IEEE international joint conference on neural network (IJCNN), Vancouver
Ucak K, Oke G (2011) Adaptive PID controller based on online LSSVR with kernel tuning. In: Proceedings of international symposium on innovations in intelligent systems and applications (INISTA 2011), Istanbul
Ungar LH (1990) A bioreactor benchmark for adaptive network-based process control. In: Miller WT III, Sutton RS, Werbos PJ (eds) Neural networks for control. MIT Press, Cambridge, pp 387–402
Vapnik VN (1999) An overview of statistical learning theory. IEEE Trans Neural Netw 10(5):988–999. doi:10.1109/72.788640
Wanfeng S, Shengdun Z, Yajing S (2008) Adaptive PID controller based on online LSSVM identification. In: Proceedings of IEEE/ASME international conference on advanced intelligent mechatronics (AIM 2008), Xian
Wang H, Pi D, Sun Y (2007) Online SVM regression algorithm-based adaptive inverse control. Neurocomputing 70(4–6):952–959. doi:10.1016/j.neucom.2006.10.021
Wang X, Du Z, Chen J, Pan F (2009) Dynamic modeling of biotechnical process based on online support vector machine. J Comput 4(3):251–258. doi:10.4304/jcp.4.3.251-258
Wu KP, Wang SD (2009) Choosing the kernel parameters for support vector machines by the inter-cluster distance in the feature space. Pattern Recognit 42(5):710–717. doi:10.1016/j.patcog.2008.08.030
Wu W, Chou YS (1999) Adaptive feedforward and feedback control of non-linear time-varying uncertain systems. Int J Control 72(12):1127–1138. doi:10.1080/002071799220489
Xu Z, Dai M, Meng D (2009) Fast and efficient strategies for model selection of Gaussian support vector machine. IEEE Trans Syst Man Cybern Part B Cybern 39(5):1292–1307. doi:10.1109/TSMCB.2009.2015672
Yuan X, Wang Y, Wu L (2008a) Composite feedforward-feedback controller for generator excitation system. Nonlinear Dyn 54(4):355–364. doi:10.1007/s11071-008-9334-6
Yuan XF, Wang YN, Wu LH (2008b) Adaptive inverse control of excitation system with actuator uncertainty. Neural Process Lett 27(2):125–136. doi:10.1007/s11063-007-9064-7
Zhao J, Li P, Wang XS (2009) Intelligent PID controller design with adaptive criterion adjustment via least squares support vector machine. In: Proceedings of 21st Chinese control and decision conference (CCDC 2009), Guilin
Zhicheng Z, Zhiyuan L, Zhimin X, Jinggang Z (2012) Internal model control based on LS-SVM for a class of nonlinear process. Phys Procedia 25:1900–1908. doi:10.1016/j.phpro.2012.03.328
Zhiying D, Xianfang W (2008) Nonlinear generalized predictive control based on online SVR. In: Proceedings of 2nd international symposium on intelligent information technology application, Shanghai
Zhong W, Pi D, Sun Y, Xu C, Chu S (2006) SVM based internal model control for nonlinear systems. In: Proceedings of 3rd international symposium on neural networks (ISNN 2006), Chengdu
Author information
Authors and Affiliations
Corresponding author
Additional information
Communicated by V. Loia.
Rights and permissions
About this article
Cite this article
Uçak, K., Öke Günel, G. An adaptive support vector regressor controller for nonlinear systems. Soft Comput 20, 2531–2556 (2016). https://doi.org/10.1007/s00500-015-1654-0
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00500-015-1654-0