Abstract
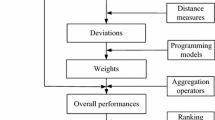
In multiple attribute decision making (MADM), hesitant fuzzy sets (HFSs) are powerful tools for expressing uncertain and vague information. Recently, MADM problems with hesitant fuzzy information have attracted increasing attention, and many MADM methods have been developed. However, only a limited amount of research has considered MADM problems that simultaneously determine attribute weights and decision-maker (DM) preferences. Therefore, we propose an MADM approach for such problems under a hesitant fuzzy environment. First, we derive extended distance and correlation coefficient measures for HFSs that are more reasonable and effective when the DM preferences are considered. We then apply the extended distance measure to subjective and objective preference information to determine attribute weights, and use these to calculate the weighted correlation coefficient between the ideal choice and each alternative. Further, we determine the ranking order of all alternatives, from which it is easy to identify the best choice. Finally, we present an example that demonstrates the practicality of the proposed approach.
Similar content being viewed by others
Explore related subjects
Discover the latest articles, news and stories from top researchers in related subjects.References
Atanassov KT (1986) Intuitionistic fuzzy sets. Fuzzy Sets Syst 20:87–96
Chen N, Xu ZS, Xia MM (2013) Correlation coefficients of hesitant fuzzy sets and their applications to clustering analysis. Appl Math Model 37:2197–2211
Farhadinia B (2013) A novel method of ranking hesitant fuzzy values for multiple attribute decision-making problems. Int J Intell Syst 28:752–767
Gu X, Wang Y, Yang B (2011) A method for hesitant fuzzy multiple attribute decision making and its application to risk investment. J Convergence Inf Technol 6:282–287
Ivor GG (1976) Fuzzy membership mapped onto intervals and many-valued quantities. Z math logik grundlagen math 22:149–160
Li DF, Cheng CT (2002) New similarity measures of intuitionistic fuzzy sets and application to pattern recognitions. Pattern Recognit Lett 23:221–225
Liao HC, Xu ZS, Zeng XJ (2014) Distance and similarity measures for hesitant fuzzy linguistic term sets and their application in multi-criteria decision making. Inf Sci 271:125–142
Liu S, Chan FTS, Ran WX (2013) Multi-attribute group decision-making with multi-granularity linguistic assessment information: An improved approach based on deviation and TOPSIS. Appl Math Model 37:10129–10140
Mizumoto M, Tanaka K (1976) Some properties of fuzzy sets of type-2. Inf Control 31:312–340
Pal SK, King RA (1981) Image enhancement using smoothing with fuzzy sets. IEEE Trans Syst Man Cybern 11:495–501
Szmidt E, Kacprzyk J (2001) Intuitionistic fuzzy sets in intelligent data analysis for medical diagnosis. In: Alexandrov VA et al (eds) CCS 2001, LNCS, Springer-Verlag, Berlin, Heidelberg, 2074:263–271
Torra V, Narukawa Y (2009) On hesitant fuzzy sets and decision. In: The 18th IEEE international conference on fuzzy systems, Jeju Island, Korea 1–3:1378–1382
Torra V (2010) Hesitant fuzzy sets. Int J Intell Syst 25:529–539
Wang TJ, Lu ZD, Li F (2002) Bidirectional approximate reasoning based on weighted similarity measures of vague sets. J Comput Eng Sci 24:96–100
Wang XR, Gao ZH, Zhao XF, Wei GW (2011) Model for evaluating the government archives website’s construction based on the GHFHWD measure with hesitant fuzzy information. Int J Digit Content Technol Appl 5:418–425
Wei GW (2012) Hesitant fuzzy prioritized operators and their application to multiple attribute group decision making. Knowl-Based Syst 31:176–182
Wei GW, Zhao XF, Wang HJ, Lin R (2012) Hesitant fuzzy Choquet integral aggregation operators and their applications to multiple attribute decision making. Information-Tokyo 15:441–448
Xia MM, Xu ZS (2011) Hesitant fuzzy information aggregation in decision making. Int J Approx Reason 52:395–407
Xiao S (2014) Induced interval-valued intuitionistic fuzzy Hamacher ordered weighted geometric operator and their application to multiple attribute decision making. J Intell Fuzzy Syst 27:527–534
Xu ZS (2010) A method based on distance measure for interval-valued intuitionistic fuzzy group decision making. Inf Sci 180:181–190
Xu ZS, Xia MM (2011a) Distance and similarity measures for hesitant fuzzy sets. Inf Sci 181:2128–2138
Xu ZS, Xia MM (2011b) On distance and correlation measures of hesitant fuzzy information. Int J Intell Syst 26:410–425
Xu ZS, Xia MM (2012) Hesitant fuzzy entropy and cross-entropy and their use in multiattribute decision-making. Int J Intell Syst 27:799–822
Xu ZS, Zhang XL (2013) Hesitant fuzzy multi-attribute decision making based on TOPSIS with incomplete weight information. Knowl-Based Syst 52:53–64
Yager RR (1988) On ordered weighted averaging aggregation operators in multi-criteria decision making. IEEE Trans Syst Man Cybern 18:183–190
Ye J (2010a) Fuzzy decision-making method based on the weighted correlation coefficient under intuitionistic fuzzy environment. Eur J Oper Res 205:202–204
Ye J (2010b) Multicriteria fuzzy decision-making method using entropy weights-based correlation coefficients of interval-valued intuitionistic fuzzy sets. Appl Math Model 34:3864–3870
Ye J (2014) Correlation coefficient of dual hesitant fuzzy sets and its application to multiple attribute decision making. Appl Math Model 38:659–666
Yu DJ (2014) Some hesitant fuzzy information aggregation operators based on Einstein operational laws. Int J Intell Syst 29:320–340
Zhao XF, Lin R, Wei GW (2014) Hesitant triangular fuzzy information aggregation based on Einstein operations and their application to multiple attribute decision making. Expert Syst Appl 41:1086–1094
Zhang XL, Xu ZS (2014) The TODIM analysis approach based on novel measured functions under hesitant fuzzy environment. Knowl-Based Syst 61:48–58
Zhu B, Xu ZS, Xia MM (2012) Hesitant fuzzy geometric Bonferroni means. Inf Sci 205:72–85
Acknowledgments
This work was supported by the Shanghai Committee of Science and Technology, China (Grant No. 13692107200).
Author information
Authors and Affiliations
Corresponding author
Additional information
Communicated by V. Loia.
Rights and permissions
About this article
Cite this article
Tong, X., Yu, L. MADM based on distance and correlation coefficient measures with decision-maker preferences under a hesitant fuzzy environment. Soft Comput 20, 4449–4461 (2016). https://doi.org/10.1007/s00500-015-1754-x
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00500-015-1754-x