An uncertain furniture production planning problem with cumulative service levels

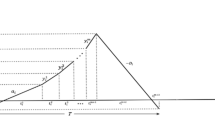
Abstract

To investigate how the loss averse customer’s psychological satisfaction affects the company’s furniture production planning, we establish a furniture production planning model under uncertain environment, where customer demand and production costs are characterized by mutually independent uncertain variables. Based on prospect theory, customer’s psychological satisfaction about stockout performance is measured by cumulative service levels in our model. In the framework of uncertainty theory, the proposed uncertain model can be transformed into an equivalent deterministic form. However, the transformed model is a nonlinear mixed integer programming problem, which cannot be solved by conventional optimization algorithms. To cope with this difficulty, a chemical reaction optimization algorithm integrated with LINGO software is designed to solve the proposed production planning problem. In order to verify the effectiveness of the designed hybrid chemical reaction optimization (CRO) algorithm, we conduct several numerical experiments via an application example and compare with a spanning tree-based genetic algorithm (hst-GA). The computational results show that our proposed CRO algorithm achieves better performance than hst-GA, and the results also provide several interesting managerial insights in production planning problems.

Appendix: Preliminaries on uncertainty theory

Let $\Gamma$ be a nonempty set, and $\mathcal {L}$ a $\sigma$-algebra over $\Gamma$. Each element $\Lambda$ in $\mathcal {L}$ is called an event. Liu (2007) defined an uncertain measure by the following axioms:

Axiom 1. (Normality Axiom) $\mathcal {M}\{\Gamma \}=1$ for the universal set $\Gamma$.

Axiom 2. (Duality Axiom) $\mathcal {M}\{\Lambda \}+\mathcal {M}\{\Lambda ^{c}\}=1$ for any event $\Lambda$.

Axiom 3. (Subadditivity Axiom) For every countable sequence of events $\Lambda _{1},\Lambda _{2},\ldots$, we have

$$\begin{aligned} \mathcal {M}\left\{ \bigcup _{i=1}^{\infty }\Lambda _{i} \right\} \le {\displaystyle \sum _{i=1}^{\infty }}\mathcal {M}\{\Lambda _{i}\}. \end{aligned}$$

The triplet $(\Gamma ,\mathcal {L},\mathcal {M})$ is called an uncertainty space. Furthermore, Liu (2009) defined a product uncertain measure by the fourth axiom:

Axiom 4. (Product Axiom) Let $(\Gamma _{k},\mathcal {L}_{k},\mathcal {M}_{k})$ be uncertainty space for $k=1,2,\cdots$. The product uncertain measure $\mathcal {M}$ is an uncertain measure satisfying

$$\begin{aligned} \mathcal {M}\left\{ \prod _{k=1}^{\infty }\Lambda _{i} \right\} = {\displaystyle \bigwedge _{k=1}^{\infty }}\mathcal {M}\{\Lambda _{k}\}, \end{aligned}$$

where $\Lambda _{k}$ are arbitrarily chosen events from $\mathcal {L}_{k}$ for $k=1,2,\ldots$, respectively.

Definition 1

(Liu 2007) An uncertain variable is a measurable function $\xi$ from an uncertainty space $(\Gamma ,\mathcal {L},\mathcal {M})$ to the set of real numbers, i.e., for any Borel set $\mathcal {B}$ of real numbers, the set

$$\begin{aligned} \{\xi \in \mathcal {B}\}=\{\gamma \in \Gamma |\xi (\gamma )\in \mathcal {B}\} \end{aligned}$$

is an event.

Definition 2

(Liu 2007) The uncertainty distribution $\mathrm{\Phi }$ of an uncertain variable $\xi$ is defined by

$$\begin{aligned} \mathrm{\Phi }(x)=\mathcal {M}\{\xi \le x\} \end{aligned}$$

for any real number x.

Definition 3

(Liu 2010) An uncertainty distribution $\mathrm{\Phi (x)}$ is said to be regular if it is a continuous and strictly increasing function with respect to x at which $0<\mathrm{\Phi }(x)<1$, and

$$\begin{aligned} \lim _{x\rightarrow -\infty }\mathrm{\Phi }(x)=0,\ \ \lim _{x\rightarrow +\infty }\mathrm{\Phi }(x)=1. \end{aligned}$$

Example 1

(Liu 2013) An uncertain variable $\xi$ is called linear if it has a linear uncertainty distribution

$$\begin{aligned} \Phi (x)= {\left\{ \begin{array}{ll} 0, &{} \quad \text {if } x \le a \\ (x-a)/(b-a), &{} \quad \text {if } a \le x \le b\\ 1, &{} \quad \text {if } x \ge b. \end{array}\right. } \end{aligned}$$

(39)

denoted by $\mathcal {L}(a,b)$ where a and b are real numbers with $a < b$.

Example 2

(Liu 2013) An uncertain variable $\xi$ is called zigzag if it has a zigzag uncertainty distribution

$$\begin{aligned} \Phi (x)= {\left\{ \begin{array}{ll} 0, &{} \quad \text {if } x \le a \\ (x-a)/2(b-a), &{} \quad \text {if } a \le x \le b\\ (x + c-2b)/2(c-b), &{} \quad \text {if } b \le x \le c\\ 1, &{} \quad \text {if } x \ge c. \end{array}\right. } \end{aligned}$$

(40)

denoted by $\mathcal {Z}(a, b, c)$ where a,b, c are real numbers with $a < b < c$.

Example 3

(Liu 2013) An uncertain variable $\xi$ is called normal if it has a zigzag uncertainty distribution

$$\begin{aligned} \Phi (x)= \left( 1+exp \left( \frac{\pi (e-x)}{\sqrt{3}\sigma } \right) \right) ^{-1}, \quad x \in \mathfrak {R} \end{aligned}$$

(41)

denoted by $\mathcal {N}(e,\sigma )$ where e and $\sigma$are real numbers with $\sigma >0$.

Example 4

(Liu 2013) An uncertain variable $\xi$ is called lognormal if ln $\xi$ is a normal uncertain variable $\mathcal {N}(e, \sigma )$. In other words, a lognormal uncertain variable has an uncertainty distribution

$$\begin{aligned} \Phi (x)= \left( 1+exp \left( \frac{\pi (e-ln x)}{\sqrt{3}\sigma } \right) \right) ^{-1}, \quad x \in \mathfrak {R} \end{aligned}$$

(42)

denoted by $\mathcal {LOGN}(e,\sigma )$ where e and $\sigma$are real numbers with $\sigma >0$.

Definition 4

(Liu 2010) Let $\xi$ be an uncertain variable with regular uncertainty distribution $\mathrm{\Phi }$. Then the inverse function $\mathrm{\Phi }^{-1}(\alpha )$ is called the inverse uncertainty distribution of $\xi$.

Definition 5

(Liu 2007) Let $\xi$ be an uncertain variable. Then the expected value of $\xi$ is defined by

$$\begin{aligned} E[\xi ]=\int _{0}^{+\infty }\mathcal {M}\{\xi \ge x\}{\text{ d }}x-\int _{-\infty }^{0}\mathcal {M}\{\xi \le x\}{\text{ d }}, x \end{aligned}$$

provided that at least one of the two integrals is finite. If $\xi$ has an uncertainty distribution $\mathrm{\Phi }$, then the expected value may be calculated by

$$\begin{aligned} E[\xi ]=\int _{0}^{+\infty }(1-\mathrm{\Phi }(x)){\text{ d }}x-\int _{-\infty }^{0}\mathrm{\Phi }(x){\text{ d }}x \end{aligned}$$

or equivalently,

$$\begin{aligned} E[\xi ]=\int _{-\infty }^{+\infty }x{\text{ d }}\Phi (x). \end{aligned}$$

If $\mathrm{\Phi }$ is also regular, then

$$\begin{aligned} E[\xi ]=\int _{0}^{1}\mathrm{\Phi }^{-1}(\alpha ){\text{ d }}\alpha . \end{aligned}$$

Theorem 3

(Liu 2007) Let $\xi _{1}$ and $\xi _{2}$ be independent uncertain variables with finite expected values. Then for any real number a and b, we have

$$\begin{aligned} E [a\xi _{1}+b\xi _{2}]=a E[\xi _{1}] + b E[\xi _{2}]. \end{aligned}$$

Theorem 4

(Liu and Ha 2010) Let $\xi$ be an uncertain variable with regular uncertainty distribution $\mathrm{\Phi }$, and let g(x) be a strictly monotone (increasing or decreasing) function; then the expected value of $g(\xi )$ is

$$\begin{aligned} E[g(\xi )]={\displaystyle \int _{-\infty }^{+\infty }}g(x)~\mathrm{d\Phi }(x). \end{aligned}$$

Definition 6

(Liu 2009) The uncertain variables $\xi _{1},\xi _{2},\ldots ,\xi _{m}$ are said to be independent if

$$\begin{aligned} \mathcal {M}\left\{ \bigcap _{i=1}^{m}(\xi _{i}\in \mathcal {B}_{i}) \right\} = {\displaystyle \bigwedge _{i=1}^{m}}\mathcal {M}\{\xi _{i}\in \mathcal {B}_{i}\}, \end{aligned}$$

for any Borel sets $\mathcal {B}_{1},\mathcal {B}_{2},\ldots ,\mathcal {B}_{m}$ of real numbers. More generally, the independence of uncertain vectors was given by Liu (2013).

Theorem 5

(Liu 2010) Let $\xi _{1},\xi _{2},\ldots ,\xi _{n}$ be independent uncertain variables with regular uncertainty distributions $\mathrm{\Phi }_{1},\mathrm{\Phi }_{2},\ldots ,\mathrm{\Phi }_{n}$, respectively. If the function $f(x_{1},x_{2},\ldots ,x_{n})$ is strictly increasing with respect to $x_{1},x_{2},\ldots ,x_{m}$ and strictly decreasing with respect to $x_{m+1},x_{m+2},\ldots ,x_{n}$, then

$$\begin{aligned} \xi =f(\xi _{1},\xi _{2},\ldots ,\xi _{n}) \end{aligned}$$

is an uncertain variable with an inverse uncertainty distribution

$$\begin{aligned} \mathrm{\Phi }^{-1}(\alpha )= & {} f(\mathrm{\Phi }_{1}^{-1}(\alpha ),\ldots ,\mathrm{\Phi }_{m}^{-1}(\alpha ),\mathrm{\Phi }_{m+1}^{-1}(1-\alpha ),\ldots ,\\&\mathrm{\Phi }_{n}^{-1}(1-\alpha )). \end{aligned}$$

and the expected value

$$\begin{aligned} E[ \xi ]= & {} \displaystyle \int _{0}^{1}f(\mathrm{\Phi }_{1}^{-1}(\alpha ),\ldots ,\mathrm{\Phi }_{m}^{-1}(\alpha ),\mathrm{\Phi }_{m+1}^{-1}(1-\alpha ),\ldots ,\\&\mathrm{\Phi }_{n}^{-1}(1-\alpha )) {\text{ d }}\alpha . \end{aligned}$$

Theorem 6

(Liu 2010) Let $\xi _{1},\xi _{2},\ldots ,\xi _{n}$ be independent uncertain variables with regular uncertainty distributions $\mathrm{\Phi }_{1},\mathrm{\Phi }_{2},\ldots ,\mathrm{\Phi }_{n}$, respectively. If the function $f(x_{1},x_{2},\ldots ,$ $x_{n})$ is strictly increasing with respect to $x_{1},x_{2},\ldots ,x_{m}$ and strictly decreasing with respect to $x_{m+1},x_{m+2},\ldots ,x_{n}$, then the chance constraint

$$\begin{aligned} \mathcal {M} \left\{ f(\xi _{1},\xi _{2},\ldots ,\xi _{n})\le 0 \right\} \ge \alpha \end{aligned}$$

holds if and only if

$$\begin{aligned} f(\mathrm{\Phi }_{1}^{-1}(\alpha ),\ldots ,\mathrm{\Phi }_{m}^{-1}(\alpha ),\mathrm{\Phi }_{m+1}^{-1}(1-\alpha ),\ldots ,\mathrm{\Phi }_{n}^{-1}(1-\alpha )) \le 0. \end{aligned}$$