Abstract
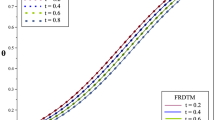
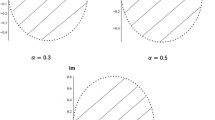
In this paper, we present a reliable multistep numerical approach, so-called Multistep Generalized Differential Transform (MsGDT), to obtain accurate approximate form solution for Rabinovich–Fabrikant model involving Caputo fractional derivative subjected to appropriate initial conditions. The solution methodology provides efficiently convergent approximate series solutions with easily computable coefficients without employing linearization or perturbation. The behavior of approximate solution for different values of fractional-order \(\alpha \) is shown graphically. Furthermore, the stability analysis of the suggested model is discussed quantitatively. Simulation of the MsGDT technique is also presented to show its efficiency and reliability. Numerical results indicate that the method is simple, powerful mathematical tool and fully compatible with the complexity of such problems.






Similar content being viewed by others
Explore related subjects
Discover the latest articles, news and stories from top researchers in related subjects.References
Agrawal SK, Srivastava M, Das S (2012) Synchronization between fractional-order Rabinovich–Fabrikant and Lotka–Volterra systems. Nonlinear Dyn 69:2277–2288
Al-Smadi M, Freihat A, Abu Arqub O, Shawagfeh N (2015) A novel multistep generalized differential transform method for solving fractional-order Lü chaotic and hyperchaotic systems. J Comput Anal Appl 19:713–724
Al-Smadi M, Abu Arqub O, Shawagfeh N, Momani S (2016) Numerical investigations for systems of secondorder periodic boundary value problems using reproducing kernel method. Appl Math Comput 291:137–148
Al-Smadi M, Freihat A, Khalil H, Momani S, Khan RA (2017) Numerical multistep approach for solving fractional partial differential equations. Int J Comput Methods 14(2):1–15. doi:10.1142/S0219876217500293
Caputo M (1967) Linear models of dissipation whose Q is almost frequency independent: Part II. Geophys J Int 13:529–539
Deng W, Li C, Lü J (2007) Stability analysis of linear fractional differentional differential system with multiple time delays. Nonlinear Dyn 48:409–416
El-Ajou A, Abu Arqub O, Al-Smadi M (2015) A general form of the generalized Taylor’s formula with some applications. Appl Math Comput 256:851–859
Ertürk VS, Momani S (2010) Application to fractional integro-differential equations. Stud Nonlinear Sci 1:118–126
Ertürk VS, Momani S, Odibat Z (2008) Application of generalized differential transform method to multi-order fractional differential equations. Commun Nonlinear Sci Numer Simul 13:1642–1654
Gafiychuk V, Datsko B (2010) Mathematical modeling of different types of instabilities in time fractional reaction–diffusion systems. Comput Math Appl 59:1101–1107
Gafiychuk V, Datsko B, Meleshko V (2008) Mathematical modeling of time fractional reaction–diffusion systems. J Comput Appl Math 220:215–225
Klafter J, Lim SC, Metzler R (2011) Fractional dynamics in physics: recent advances. World Scientific, Singapore
Klimek M (2001) Fractional sequential mechanics-models with symmetric fractional derivative. Czechoslov J Phys 51:1348–1354
Kolebaje OT, Ojo OL, Akinyemi P, Adenodi RA (2013) On the application of the multistage laplace adomian decomposition method with pade approximation to the Rabinovich–Fabrikant system. Adv Appl Sci Res 4:232–243
Laskin N (2000) Fractional quantum mechanics. Phys Rev E 62:3135–3145
Liu F, Burrage K (2011) Novel techniques in parameter estimation for fractional dynamical models arising from biological systems. Comput Math Appl 62:822–833
Liu Y, Yang Q, Pang G (2010) A hyperchaotic system from the Rabinovich system. J Comput Appl Math 234:101–113
Magin RL (2006) Fractional calculus in bioengineering. Begell House Publisher Inc, Connecticut
Mainardi F (2010) Fractional calculus and waves in linear viscoelasticity. Imperial College Press, London
Matignon D (1996) Stability results for fractional differential equations with applications to control processing. In: IMACS, IEEE-SMC Proceedings of the Computational Engineering in Systems and Application Multiconference, vol 2. Lille, pp 963–968
Millar KS, Ross B (1993) An introduction to the fractional calculus and fractional differential equations. Wiley, New York
Momani S, Odibat Z, Ertürk VS (2007) Generalized differential transform method for solving a space- and time-fractional diffusion-wave equation. Phys Lett A 370:379–387 V.S. Ertürk, S. Momani, On the Generalized Differential
Momani S, Freihat A, AL-Smadi M (2014) Analytical study of fractional-order multiple chaotic FitzHugh–Nagumo neurons model using multi-step generalized differential transform method. Abstract Appl Anal 2014, Article ID 276279, 1-10
Odibat Z, Momani S (2008) A generalized differential transform method for linear partial differential equations of fractional order. Appl Math Lett 21:194–199
Odibat Z, Shawagfeh N (2007) Generalized Taylor’s formula. Appl Math Comput 186:286–293
Odibat ZM, Bertelle C, Aziz-Alaoui MA, Duchamp GHE (2010) A multi-step differential transform method and application to non chaotic or chaotic systems. Comput Math Appl 59:1462–1472
Ortigueira MD (2010) The fractional quantum derivative and its integral representations. Commun Nonlinear Sci Numer Simul 15:956–962
Petras I (2010) A note on the fractional-order Volta’s system. Commun Nonlinear Sci Numer Simul 15:384–393
Podlubny I (1999) Fractional differential equations. Academic Press, San Diego
Rabinovich MI, Fabrikant AL (1979) Stochastic self-modulation of waves in nonequilibrium media. Sov Phys JETP 50:311–317
Srivastava M, Agrawal S, Vishal K, Das S (2014) Chaos control of fractional order Rabinovich–Fabrikant system and synchronization between chaotic and chaos controlled fractional order Rabinovich–Fabrikant system. Appl Math Model 38:3361–3372
Tarasov VE (2011) Fractional dynamics: applications of fractional calculus to dynamics of particles, fields and media. Springer, Berlin
Tavazoei MS, Haeri M (2007) A necessary condition for double scroll attractor existence in fractional-order systems. Phys Lett A 367:102–113
Tavazoei MS, Haeri M (2008) Chaotic attractors in incommensurate fractional order systems. Physica D 237:2628–2637
Zhen W, Xia H, Guodong S (2011) Analysis of nonlinear dynamics and chaos in a fractional order financial system with time delay. Comput Math Appl 62:1531–1539
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
The authors declare that there is no conflict of interests regarding the publication of this paper.
Additional information
Communicated by V. Loia.
Rights and permissions
About this article
Cite this article
Moaddy, K., Freihat, A., Al-Smadi, M. et al. Numerical investigation for handling fractional-order Rabinovich–Fabrikant model using the multistep approach. Soft Comput 22, 773–782 (2018). https://doi.org/10.1007/s00500-016-2378-5
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00500-016-2378-5