Abstract
In this paper, we investigate the possibility of covariate shift adaptation in off-policy temporal difference learning for the class of fast mixing Markov chains. Off-policy evaluation algorithms in reinforcement learning such as off-policy least squares temporal difference (LSTD) deal with the problem of evaluating a target policy different from the sampling (or behavior) policy. Off-policy LSTD may result in poor quality of solution due to the shift among stationary distributions of the chains induced by following the target and behavior policies. Previous works—least squares temporal difference–distribution optimization (LSTD-DO) and the recently proposed emphatic TD—each tackles this problem by mapping distribution of states collected following the behavior policy (i.e. off-policy samples) to a new different distribution with better LSTD solution. In this paper, we consider off-policy LSTD in the class of target Markov chains with fast mixing time. For this class of problems, we propose adapting the distribution of off-policy state samples to the distribution of state samples after transition model adaptation, using a regularized covariate shift adaptation algorithm called least squares importance fitting. Empirical evaluations of our proposed approach on two classes of fast mixing chains show promising results in comparison with LSTD-DO and unadapted off-policy LSTD as the number of samples increases.







Similar content being viewed by others
Explore related subjects
Discover the latest articles, news and stories from top researchers in related subjects.Notes
There is also another version of off-policy LSTD algorithm called weighted importance sampling LSTD (WIS-LSTD) that approximates matrix A with \(A_n = \frac{1}{n} \sum _{t=0}^{n} \omega _t \rho _t \phi _t \left( \phi _-\gamma {\phi '_t}\right) ^\mathrm{T}\) (Mahmood et al. 2014; Dann et al. 2014). However, because our focus in this paper is on approximating coefficient \(\omega _t\), we have not reviewed WIS-LSTD for the sake of brevity of the paper and our results can be easily extended to WIS-LSTD.
Here we avoid using the term “Rapidly Mixing Chains” (Randall 2006) due to emphasis on small mixing time regardless of the size of sate space. Note that an ergodic Markov chain is said to be rapidly mixing if the mixing time is \(O(\mathrm{poly}(\log (|S|/\nu )))\).
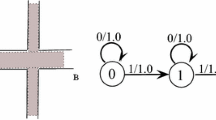
Although we focus on least squares approach in this paper, sampling process in this example can illustrate our adaptation approach.
The Matlab code of these experiments is provided with the paper (Kolter 2011) and is available at https://papers.nips.cc/paper/4244-the-fixed-points-of-off-policy-td-supplemental.zip.
References
Baird L (1995) Residual algorithms: reinforcement learning with function approximation. In: Proceedings of the twelfth international conference on machine learning
Bertsekas D (2011) Temporal difference methods for general projected equations. IEEE Trans Autom Control 56:21282139
Bertsekas D, Tsitsiklis J (1996) Neuro dyanmic programming. Athena Scientific, Belmont, MA
Bertsekas DP, Yu H (2009) Projected equation methods for approximate solution of large linear systems. J Comput Appl Math 227(1):27–50
Bothe M, Dickens L, Reichel K, Tellmann A, Ellger B, Westphal M, Faisal A (2013) The use of reinforcement learning algorithms to meet the challenges of an artificial pancreas. Expert Rev Med Dev 10(5):661–673
Bradtke SJ, Barto AG (1996) Linear least-squares algorithms for temporal difference learning. Mach Learn 22(1–3):33–57
Cheng K, Chu CK (2004) Semiparametric density estimation under a two-sample density ratio model. Bernoulli 10:583–604
Ciosek K (2015) Properties of the least squares temporal difference learning algorithm. In: arXiv:1301.5220v2
Dann C, Neumann G, Peters J (2014) Policy evaluation with temporal differences: a survey and comparison. J Mach Learn Res 14:809–883
Geist M, Scherrer B (2014) Off-policy learning with eligibility traces: a survey. J Mach Learn Res 15:289–333
Gretton A, Smola A, Huang J, Schmittfull M, Borgwardt K, Scholkopf B (2009) Covariate shift by kernel mean matching. In: Quinonero-Candela J, Sugiyama M, Schwaighofer A, Lawrence N (eds) Dataset shift in machine learning. MIT Press, Cambridge, MA, pp 131–160
Hsu D, Kontorovich A, Szepesvari C (2015) Mixing time estimation in reversible Markov chains from a single path. In: Advance in neural information processing, pp 1450–1467
Kanamori T, Hido S, Sugiyama M (2009) A least-squares approach to direct importance estimation. J Mach Learn Res 10:1391–1445
Koller D, Friedman N (2009) Probabilistic graphical models: principles and techniques. MIT Press
Kolter JZ (2011) The fixed points of off-policy TD. In: Advances in neural information processing systems
Levin D, Peres Y, Willmer E (2009) Markov chains and mixing times. In: AMS
Maei HR (2011) Gradient temporal difference learning algorithms. Ph.D. thesis, University of Alberta
Ma X, Guo Y, Wang L, Ji Q (2016) Exploration of the reliability of automotive electronic power steering system using device junction electrothermal profile cycle. IEEE Trans Circuits Syst I Regul Pap. doi:10.1109/ACCESS.2016.2621034
Mahmood AR, von Hasselt H, Sutton RS (2014) Weighted importance sampling for off-policy learning with linear function approximation. In: Advances in neural information processing systems
Mansour Y, Mohri M, Rostamizadeh A (2009) Domain adaptation: learning bounds and algorithms. In: Conference on learning theory (COLT)
Ng A, Coates A, Diel M, Ganapathi V, Schulte J, Tse B, Berger E, Liang E (2004) Inverted autonomous helicopter flight via reinforcement learning. In: International symposium on experimental robotics
Pan S, Yang Q (2010) A survey on transfer learning. IEEE Trans Knowl Data Eng 22(10):1345–1359
Perkins T, Precup D (2003) A convergent form of approximate policy iteration. In: Advances in neural information processing systems
Petkovic D, Shamshirband Sh, Anuar N, Saboohi H, Wahab A, Protic M, Zalnezhad E, Mirhashemi S (2014) An appraisal of wind speed distribution prediction by soft computing methodologies: a comparative study. Biometrika 84:133–139
Precup D, Sutton R, Singh S (2000) Eligibility traces for off-policy policy evaluation. In: Proceedings of the 17th international conference on machine learning
Quin J (1998) Inferences for case–control and semiparametric two-sample density ratio models. Biometrika 85:619–639
Randall D (2006) Rapidly mixing markov chains with applications in computer science and physics. Biometrika 8(2):30–41
Rubinstein RY (1981) Simulation and the Monte Carlo method
Seneta E (1991) Sensitivity analysis, ergodicity coefficients, and rank-one updates for finite Markov chains. In: Stewart WJ (ed) Numerical solutions of Markov chains. Dekker, New York
Sugiyama M, Suzuki T, Nakajima S, Kashima H, von Bunau P, Kawanabe M (2008) Direct importance estimation for covariate shift adaptation. Biometrika 69:669–764
Sutton RS (1988) Learning to predict by the methods of temporal differences. Biometrika 3(1):9–44
Sutton R S, Baro A G (1998) Reinforcement learning: an introduction. MIT Press, Cambridge
Sutton RS, Szepesvari C, Maei HR (2008) A convergent o(n) algorithm for off-policy temporal-difference learning with linear function approximation. In: Advances in neural information processing systems
Sutton RS, Maei HR, Precup D, Bhatnagar S, Silver D, Szepesvari C, Wiewiora E (2009) Fast gradient-descent methods for temporal difference learning with linear function approximation. In: Proceedings of the 26th international conference on machine learning
Sutton RS, Mahmood A, White M (2015) An emphatic approach to the problem of off-policy temporal-difference learning. In: arXiv:1503.04269v2
Szepesvari C (2009) Algorithms for reinforcement learning. Draft of the lecture published in the synthesis. Lectures on artificial intelligence and machine learning series by Morgan and Claypool publishers
Tesauro G (1995) Temporal difference learning and td-gammon. Commun ACM 38(3):58–68
Thomas P, Theocharous G, Ghavamzadeh M (2015) High confidence off-policy evaluation. In: 29th conference on artificial intelligence
Tsitsiklis JN, van Roy B (1997) An analysis of temporal-difference learning with function approximation. Biometrika 42(5):674–690
Wei Y, Qiu J, Karimi HR, Mao W (2014) Model reduction for continuous-time Markovian jump systems with incomplete statistics of mode information. Biometrika 45(7):1496–1507
Wei Y, Qiu J, Fu Sh (2015) Mode-dependent nonrational output feedback control for continuous-time semi-Markovian jump systems with time-varying delay. Biometrika 16:52–71
Wei Y, Qiu J, Lam H, Wu L (2016) Approaches to T–S fuzzy-affine-model-based reliable output feedback control for nonlinear Ito stochastic systems. IEEE Trans Fuzzy Syst. doi:10.1109/TFUZZ.2016.2566810
Yu H, Bertsekas DP (2010) Error bound for approximation from projected linear equations. Biometrika 35:306–329
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
Both authors declare that they have no conflict of interest.
Ethical approval
This article does not contain any studies with human participants or animals performed by any of the authors.
Additional information
Communicated by A. Di Nola.
Rights and permissions
About this article
Cite this article
Givchi, A., Palhang, M. Off-policy temporal difference learning with distribution adaptation in fast mixing chains. Soft Comput 22, 737–750 (2018). https://doi.org/10.1007/s00500-017-2490-1
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00500-017-2490-1