Abstract
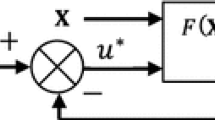
In this paper a robust hybrid observer-based hybrid adaptive fuzzy controller for large-scale multiple-input multiple-output (MIMO) systems with affine and nonaffine form in the presence of input saturation is presented. Based on an arbitrary control gain matrix, a hybrid control scheme is designed to avoid the possible singularity problem. The proposed control method is very simple, effective and robust. The states of the system and the mathematical model of the system under control do not need to be well known. An observer-based adaptive fuzzy system based on strictly positive real (SPR) theory is applied to approximate the system states, but it does not require SPR conditions to be known identified. A robust control term is utilized to compensate the both uncertainties and observer errors and attenuate the residual error to the desired level. Finally, to display the applicability and efficiency of the proposed control method, a MIMO affine system and a MIMO nonaffine system with input saturation are applied in simulations.















Similar content being viewed by others
Explore related subjects
Discover the latest articles, news and stories from top researchers in related subjects.References
Aghababa MP (2016) Optimal design of fractional-order PID controller for five bar linkage robot using a new particle swarm optimization algorithm. Soft Comput 20:4055–4067
Arefi MM, Jahed Motlagh MR (2013) Observer based adaptive neural control of uncertain MIMO nonlinear systems with unknown control direction. Int J Adapt Control Signal Process 27:741–754
Arefi MM, Zarei J, Karimi HR (2014) Adaptive output feedback neural network control of uncertain non-affine systems with unknown control direction. J Frankl Inst 351:4302–4316. doi:10.1016/j.jfranklin.2014.05.006
Boulkroune A, Tadjine M, M’Saad M, Farza M (2008) How to design a fuzzy adaptive controller based on observers for uncertain affine nonlinear systems. Fuzzy Sets Syst 159:926–948
Chang Y-C (2000) Robust tracking control for nonlinear MIMO systems via fuzzy approaches. Automatica 36:1535–1545
Chen M, Ge SS (2013) Direct adaptive neural control for a class of uncertain nonaffine nonlinear systems based on disturbance observer. IEEE Trans Cyber 43:1213–1225
de Moura Oliveira PB, Freire H, Pires EJS (2016) Grey wolf optimization for PID controller design with prescribed robustness margins. Soft Comput 20:4243–4255
Du H, Chen X (2009) NN-based output feedback adaptive variable structure control for a class of non-affine nonlinear systems: A nonseparation principle design. Neurocomputing 72:2009–2016. doi:10.1016/j.neucom.2008.12.015
Fan X, Yi Y, Ye Y (2017) DOB tracking control for systems with input saturation and exogenous disturbances via TS disturbance modelling. In: Chang D, Wei B (eds) Mechatronics and robotics engineering for advanced and intelligent manufacturing. Springer, Berlin, pp 445–455. doi:10.1007/978-3-319-33581-0_35
Feng Y, Yu X, Man Z (2002) Non-singular terminal sliding mode control of rigid manipulators. Automatica 38:2159–2167
Fuh C-C (2009) Optimal control of chaotic systems with input saturation using an input-state linearization scheme. Commun Nonlinear Sci Numer Simul 14:3424–3431
Gao Y, Tong S (2015) Composite adaptive fuzzy output feedback dynamic surface control design for uncertain nonlinear stochastic systems with input quantization. Int J Fuzzy Syst 17:609–622
Ghavidel HF, Kalat AA (2017a) Observer-based hybrid adaptive fuzzy control for affine and non-affine uncertain nonlinear systems. Neural Comput Appl. doi:10.1007/s00521-016-2732-7
Ghavidel HF, Kalat AA (2017b) Observer-based robust composite adaptive fuzzy control by uncertainty estimation for a class of nonlinear systems. Neurocomputing. doi:10.1016/j.neucom.2016.12.001
Ghavidel HF, Kalat AA (2017c) Robust composite adaptive fuzzy identification control of uncertain MIMO nonlinear systems in the presence of input saturation. Arab J Sci Eng. doi:10.1007/s13369-017-2552-9
Ghavidel HF, Kalat AA (2017d) Robust control for MIMO hybrid dynamical system of underwater vehicles by composite adaptive fuzzy estimation of uncertainties. Nonlinear Dyn. doi:10.1007/s11071-017-3590-2
Ghavidel HF, Kalat AA, Ghorbani V (2017e) Observer-based robust adaptive fuzzy approach for current control of robot manipulators by estimation of uncertainties. Modares Mech Eng 17:286–294
Huang Y-S, Liu W-P, Wu M, Wang Z-W (2014) Robust decentralized hybrid adaptive output feedback fuzzy control for a class of large-scale MIMO nonlinear systems and its application to AHS. ISA Trans 53:1569–1581
Javidan R, Khuban H (2016) Optimal non-integer PID controller for a class of nonlinear systems: multi-objective modified black hole optimization algorithm. Neural Comput Appl. doi:10.1007/s00521-016-2691-z
Kumbasar T (2014) A simple design method for interval type-2 fuzzy PID controllers. Soft Comput 18:1293–1304
Labiod S, Boucherit MS, Guerra TM (2005) Adaptive fuzzy control of a class of MIMO nonlinear systems. Fuzzy sets Syst 151:59–77
Li H-X, Tong S (2003) A hybrid adaptive fuzzy control for a class of nonlinear MIMO systems. IEEE Trans Fuzzy Syst 11:24–34
Li Y, Tong S, Li T (2014) Adaptive fuzzy output-feedback control for output constrained nonlinear systems in the presence of input saturation. Fuzzy Sets Syst 248:138–155
Li Y, Tong S, Li T (2013) Direct adaptive fuzzy backstepping control of uncertain nonlinear systems in the presence of input saturation. Neural Comput Appl 23:1207–1216. doi:10.1007/s00521-012-0993-3
Li Y, Tong S, Li T (2015) Composite adaptive fuzzy output feedback control design for uncertain nonlinear strict-feedback systems with input saturation. IEEE Trans Cybern 45:2299–2308
Lin TC (2010) Observer-based robust adaptive interval type-2 fuzzy tracking control of multivariable nonlinear systems. Eng Appl Artif Intell 23:386–399. doi:10.1016/j.engappai.2009.11.007
Mohammad-Hoseini S, Farrokhi M, Koshkouei AJ (2008) Robust adaptive control of uncertain non-linear systems using neural networks. Int J Control 81:1319–1330. doi:10.1080/00207170701771885
Nekoukar V, Erfanian A (2011) Adaptive fuzzy terminal sliding mode control for a class of MIMO uncertain nonlinear systems. Fuzzy Sets Syst 179:34–49
Park JH, Park GT, Kim SH, Moon CJ (2005) Direct adaptive self-structuring fuzzy controller for nonaffine nonlinear system. Fuzzy Sets Syst 153:429–445. doi:10.1016/j.fss.2005.01.003
R. Parks T (1991) Manual For Model 730 Magnetic Levitation System. Educ Control Prod 197
Shahnazi R (2014) Output feedback adaptive fuzzy control of uncertain MIMO nonlinear systems with unknown input nonlinearities. ISA Trans 54:39–51. doi:10.1016/j.isatra.2014.07.006
Shahnazi R (2016) Observer-based adaptive interval type-2 fuzzy control of uncertain MIMO nonlinear systems with unknown asymmetric saturation actuators. Neurocomputing 171:1053–1065
Shaocheng T, Bin C, Yongfu W (2005) Fuzzy adaptive output feedback control for MIMO nonlinear systems. Fuzzy Sets Syst 156:285–299
Shaocheng T, Jiantao T, Tao W (2000) Fuzzy adaptive control of multivariable nonlinear systems1. Fuzzy Sets Syst 111:153–167
Shen Q, Zhang T (2012) Novel design of adaptive neural network controller for a class of non-affine nonlinear systems. Commun Nonlinear Sci Numer Simul 17:1107–1116
Shi W (2014) Adaptive fuzzy control for MIMO nonlinear systems with nonsymmetric control gain matrix and unknown control direction. IEEE Trans Fuzzy Syst 22:1288–1300
Shi W (2015) Observer-based fuzzy adaptive control for multi-input multi-output nonlinear systems with a nonsymmetric control gain matrix and unknown control direction. Fuzzy Sets Syst 263:1–26
Shi W (2016) Observer-based indirect adaptive fuzzy control for SISO nonlinear systems with unknown gain sign. Neurocomputing 171:1598–1605. doi:10.1016/j.neucom.2015.08.004
Shi W, Zhang M, Guo W, Guo L (2011) Stable adaptive fuzzy control for MIMO nonlinear systems. Comput Math with Appl 62:2843–2853
Soyguder S, Karakose M, Alli H (2009) Design and simulation of self-tuning PID-type fuzzy adaptive control for an expert HVAC system. Expert Syst Appl 36:4566–4573. doi:10.1016/j.eswa.2008.05.031
Sun L, Huo W, Jiao Z (2017) Adaptive backstepping control of spacecraft rendezvous and proximity operations with input saturation and full-state constraint. IEEE Trans Ind Electron 64:480–492
Wang W, Wang D, Peng Z, Wang H (2016) Cooperative adaptive fuzzy output feedback control for synchronization of nonlinear multi-agent systems in the presence of input saturation. Asian J Control 18:619–630. doi:10.1002/asjc.1104
Wu J, Su B, Li J et al (2017) Adaptive fuzzy control for full states constrained systems with nonstrict-feedback form and unknown nonlinear dead zone. Inf Sci 376:233–247
Wu LB, Yang GH (2016) Adaptive fuzzy tracking control for a class of uncertain nonaffine nonlinear systems with dead-zone inputs. Fuzzy Sets Syst 290:1–21. doi:10.1016/j.fss.2015.05.006
Zhang J, Yang S (2016) A novel PSO algorithm based on an incremental-PID-controlled search strategy. Soft Comput 20:991–1005
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
The author declares that they have no conflict of interest.
Human participants
This article does not contain any studies with human participants or animals performed by any of the authors.
Informed consent
Informed consent was obtained from all individual participants included in the study.
Additional information
Communicated by V. Loia.
Rights and permissions
About this article
Cite this article
Ghavidel, H.F. Robust control of large-scale nonlinear systems by a hybrid adaptive fuzzy observer design with input saturation. Soft Comput 22, 6473–6487 (2018). https://doi.org/10.1007/s00500-017-2699-z
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00500-017-2699-z