Abstract
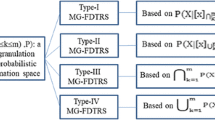
This article introduces general framework of multi-granulation bipolar-valued fuzzy (BVF) probabilistic rough sets (MG-BVF-PRSs) models in multi-granulation BVF probabilistic approximation space over two universes. Four types of MG-BVF-PRSs are established, by the four different conditional probabilities of BVF event. For different constraints on parameters, we obtain four kinds of each type MG-BVF-PRSs over two universes. To find a suitable way of explaining and determining these parameters in each kind of each type MG-BVF-PRS, three-way decisions (3WDs) are studied based on Bayesian minimum-risk procedure, i.e., the multi-granulation BVF decision-theoretic rough set (MG-BVF-DTRS) approach. The main contribution of this paper is twofold. One is to extend the fuzzy probabilistic rough set (FPRS) to MG-BVF-PRS model over two universes. Another is to present an approach to select parameters in MG-BVF-PRS modeling by using the process of decision making under conditions of risk.





Similar content being viewed by others
Explore related subjects
Discover the latest articles, news and stories from top researchers in related subjects.References
Atanassov KT (1986) Intuitionistic fuzzy sets. Fuzzy Sets Syst 20:87–96
Cacioppo JT, Gardner WL, Berntson GG (1997) Beyond bipolar conceptualizations and measures: the case of attitudes and evaluation space. Pers Soc Psychol Rev 1:3–25
Chen DG, Zhang L, Zhao SY, Hu QH, Zhu PF (2012) A novel algorithm for finding reducts with fuzzy rough sets. IEEE Trans Fuzzy Syst 20(2):385–389
Deng X, Yao Y (2014) Decision-theoretic three-way approximations of fuzzy sets. Inf Sci 279:702–715
Dou HL, Yang XB, Fan JY, Xu SP (2012) The models of variable precision multigranulation rough sets, RSKT 2012. LNCS 7414:465–473
Dubois D, Prade H (2008) An introduction to bipolar representations of information and preference. Int J Intell Syst 23:866–877
Gau WL, Tan JM (1993) Vague sets. IEEE Trans Syst Man Cybern 23:610–614
Gut A (2013) Probability—a graduate course, 2nd edn. Springer, New York
Han Y, Shi P, Chen S (2015) Bipolar-valued rough fuzzy set and its applications to decision information system. IEEE Trans Fuzzy Syst 33(6):2358–2370
Li JH, Ren Y, Mei CL, Qian YH, Yang XB (2016) A comparative study of multi-granulation rough sets and concept lattices via rule acquisition. Knowl-Based Syst 91:152–164
Liang DC, Liu D, Pedrycz W, Hu P (2013) Triangular fuzzy decision-theoretic rough sets. Int J Approx Reason 54:1087–1106
Lin GP, Qian YH, Li JJ (2012) NMGRS—neighborhood-based multigranulation rough sets. Int J Approx Reason 53(7):1080–1093
Lin GP, Liang JY, Qian YH (2013) Multigranulation rough sets: from partition to covering. Inf Sci 241:101–118
Lin YJ, Li JJ, Lin PR, Lin GP, Chen JK (2014) Feature selection via neighborhood multi-granulation fusion. Knowl-Based Syst 67:162–168
Lin G, Liang J, Qian Y, Li J (2016) A fuzzy multigranulation decision-theoretic approach to multi-source fuzzy information systems. Knowl-Based Syst 91:102–113
Ma W, Sun B (2012a) On relationship between probabilistic rough set and bayesian risk decision over two universes. Int J Gen Syst 41:225–245
Ma W, Sun B (2012b) Probabilistic rough set over two universes and rough entropy. Int J Approx Reason 53:608–619
Pawlak Z (1982) Rough set. Int J Comput Inf Sci 11:341–356
Pdrycz W (2013) Granular computing: analysis and design of intelligent systems. CRC Press, Francis Taylor, Boca Raton
Qian YH, Liang JY, Pedrycz W, Dang CY (2010a) Positive approximation: an accelerator for attribute reduction in rough set theory. Artif Intell 174:597–618
Qian YH, Liang JY, Yao YY, Dang CY (2010b) MGRS–a multi-granulation rough set. Inf Sci 180:949–970
Qian YH, Zhang H, Sang YL, Liang JY (2014) Multigranulation decision-theoretic rough sets. Int J Approx Reason 55:225–237
She YH, He XL (2012) On the structure of the multigranulation rough set model. Knowl-Based Syst 36:81–92
Sun B, Ma W, Zhao H (2014) Decision-theoretic rough fuzzy set model and application. Inf Sci 283:180–196
Sun B, Ma W, Chen X (2015) Fuzzy rough set on probabilistic approximation space over two universes and its application to emergency decision-making. Exp Syst 32:507–521
Sun B, Ma W, Zhao H (2016) An approach to emergency decision making based on decision-theoretic rough set over two universes. Soft Comput 20(9):3617–3628
Tree GD, Zadrony S, Bronselaer AJ (2010) Handling bipolarity in elementary queries to possibilistic databases. IEEE Trans Fuzzy Syst 18(3):599–612
Yang HL, Liao X, Wang S, Wang J (2013) Fuzzy probabilistic rough set model on two universes and its applications. Int J Approx Reason 54:1410–1420
Yang XB, Qi Y, Yu HL, Song XN, Yang JY (2014) Updating multigranulation rough approximations with increasing of granular structures. Knowl-Based Syst 64:59–69
Yao YY (2001) Information granulation and rough set approximation. Int J Intell Syst 16:87–104
Yao YY (2007) Decision-theoretic rough set models. Lect Notes Comput Sci 4481:1–12
Yao YY (2008) Probabilistic rough set approximations. Int J Approx Reason 49:255–271
Yao YY (2010) Three-way decisions with probabilistic rough sets. Inf Sci 180:341–353
Yao YY (2011) The superiority of three-way decisions in probabilistic rough set models. Inf Sci 181:1080–1096
Yao Y, She Y (2016) Rough set models in multigranulation spaces. Inf Sci 327:40–56
Yao YY, Wong SKW (1992) A decision theoretic framework for approximating concepts. Int J Man-Mach Stud 37:793–809
Yao YY, Zhou B (2010) Naive Bayesian rough sets. Lect Notes Comput Sci 6401:719–726
Zadeh LA (1965) Fuzzy sets. Inf Control 8:338–358
Zadeh LA (1968) Probability measures of fuzzy events. J Math Anal Appl 23:421–427
Zadeh LA (1975) The concept of a linguistic variable and its application to approximate reasoning. Inf Sci 8:199–249
Zadeh LA (1979) Fuzzy sets and information granularity. In: Gupta N, Ragade R, Yager R (eds) Advances in fuzzy set theory and applications. North-Holland, Amsterdam, pp 3–18
Zhang WR (1994) Bipolar fuzzy sets and relations: a computational framework for cognitive modeling and multiagent decision analysis. In: Proceeding of IEEE Conference, pp 305–309
Zhang WR (2011) Yin Yang bipolar relativity: a unifying theory of nature, agents and causality with application in quantum computing, cognitive informatics and life sciences. IGI Global, Hersgey and New York
Zhang WR, Zhang L (2004) Yin Yang bipolar logic and bipolar fuzzy logic. Inf Sci 165(3–4):265–287
Zhao XR, Hu BQ (2015) Fuzzy and interval-valued decision-theoretic rough set approaches based on the fuzzy probability measure. Inf Sci 298:534–554
Zhao XR, Hu BQ (2016) Fuzzy probabilistic rough sets and their corresponding three-way decisions. Knowl-Based Syst 91:126–142
Zhao SY, Tsang CC, Chen DG (2009) The model of fuzzy variable precision rough sets. IEEE Trans Fuzzy Syst 17(2):451–467
Zhao SY, Chen H, Li CP, Zhai MY (2013) RFRR—robust fuzzy rough reduction. IEEE Trans Fuzzy Syst 21(5):825–841
Ziarko W (2002) Set approximation quality measures in the variable precision rough set model. In: Proceedings of the 2nd International Conference on Hybrid Intelligent Systems (HIS”02). Soft Comput Syst 87:442–452
Ziarko W (2008) Probabilistic approach to rough sets. Int J Approx Reason 49:272–284
Acknowledgements
The authors would like to thank the Associate Editor and reviewers for their thoughtful comments and valuable suggestions. Some tables and figures are directly benefitted from the reviewers comments.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
Prasenjit Mandal and A. S. Ranadive declare that there is no conflict of interest.
Ethical approval
This article does not contain any study performed on humans or animals by the authors.
Informed consent
Informed consent was obtained from all individual participants included in the study.
Additional information
Communicated by V. Loia.
Rights and permissions
About this article
Cite this article
Mandal, P., Ranadive, A.S. Multi-granulation bipolar-valued fuzzy probabilistic rough sets and their corresponding three-way decisions over two universes. Soft Comput 22, 8207–8226 (2018). https://doi.org/10.1007/s00500-017-2765-6
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00500-017-2765-6