Abstract
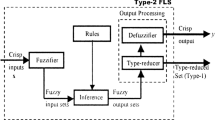
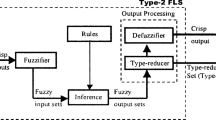
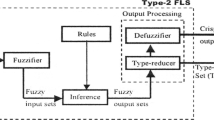
With the development of \(\alpha \)-planes representation of general type-2 fuzzy sets (GT2 FSs), general type-2 fuzzy logic systems (GT2 FLSs) based on GT2 FSs have become a hot topic in academic field. While type-reduction (TR) is most critical block for a T2 FLS, generally speaking, the most popular Karnik–Mendel (KM) or enhanced KM (EKM) algorithms are used to perform the TR. The paper connects the EKM and the continuous version of EKM algorithms together and expands the EKM algorithms to three different forms of weighted EKM (WEKM) algorithms resort to the Newton–Cotes quadrature formulas of numerical integration techniques, while the EKM algorithms just become a special case of the WEKM algorithms. Four computer simulation examples are used to illustrate the performances of the WEKM algorithms. Compared with the EKM algorithms, the WEKM algorithms have smaller absolute error and faster convergence speed to compute the centroid defuzzified value of GT2 FLSs in general, which make them potentially applicable for T2 FLSs designers and adopters.




























Similar content being viewed by others
Explore related subjects
Discover the latest articles, news and stories from top researchers in related subjects.References
Aisbett J, Rickard JT, Morgenthaler DG (2010) Type-2 fuzzy sets as functions on spaces. IEEE Trans Fuzzy Syst 18(4):841–844
Biglarbegian M, Melek WW, Mendel JM (2010) On the stability of interval type-2 TSK fuzzy logic systems. IEEE Trans Syst Man Cybern B Cybern 40(3):798–818
Biglarbegian M, Melek WW, Mendel JM (2011) Design of novel interval type-2 fuzzy controllers for modular and reconfigurable robots: theory and experiments. IEEE Trans Ind Electron 58(4):1371–1384
Bilgin A, Hagras H, Malibari A et al (2013) Towards a linear general type-2 fuzzy logic based approach for computing with words. Soft Comput 17(12):2203–2222
Caraveo C, Valdez F, Castillo O (2017) Nature-inspired design of hybrid intelligent systems. Studies in computational intelligence
Castillo O, Amador-Angulo L, Castro JR, Garcia-Valdez M (2016a) A comparative study of type-1 fuzzy logic systems, interval type-2 fuzzy logic systems and generalized type-2 fuzzy logic systems in control problems. Inf Sci 354(Part C):257–274
Castillo O, Cervantes L, Soria J et al (2016b) A generalized type-2 fuzzy granular approach with applications to aerospace. Inf Sci 354(C):165–177
Chen Y, Wang DZ (2015) Studies on centroid type-reduction algorithms for interval type-2 fuzzy logic systems. In: IEEE international conference on big data and cloud computing, pp 344–349
Chen S, Chang Y, Pan J (2013) Fuzzy rules interpolation for sparse fuzzy rule-based systems based on interval type-2 gaussian fuzzy sets and genetic algorithms. IEEE Trans Fuzzy Syst 21(3):412–425
Chen Y, Wang DZ, Ning W (2015) Studies on centroid type-reduction algorithms for general type-2 fuzzy logic systems. Int J Innov Comput Inf Control 11(6):1987–2000
Chen Y, Wang DZ, Tong SC (2016) Forecasting studies by designing Mamdani interval type-2 fuzzy logic systems: with the combination of BP algorithms and KM algorithms. Neurocomputing 174(Part B):1133–1146
Coupland S, John R (2007) Geometric type-1 and type-2 fuzzy logic systems. IEEE Trans Fuzzy Syst 15(1):3–15
Gonzalez C, Castro JR, Melin P, Castillo O (2016) An edge detection method based on generalized type-2 fuzzy logic. Soft Comput 20(2):773–784
Gonzalez CI, Melin P, Castro JR, Mendoza O, Castillo O (2017) General type-2 fuzzy edge detection in the preprocessing of a face recognition system. Springer, Berlin
Hagras H, Wagner C (2012) Towards the wide spread use of type-2 fuzzy logic systems in real world applications. IEEE Comput Intell Mag 7(3):14–24
Hidalgo D, Melin P, Castillo O (2012) An optimization method for designing type-2 fuzzy inference systems based on the footprint of uncertainty using genetic algorithms. Expert Syst Appl 39(4):4590–4598
Hsu CH, Juang CF (2013) Evolutionary robot wall-following control using type-2 fuzzy controller with species-de-activated continuous ACO. IEEE Trans Fuzzy Syst 21(1):100–112
Juang CF, Chang PH (2010) Designing fuzzy-rule-based systems using continuous ant-colony optimization. IEEE Trans Fuzzy Syst 18(1):138–149
Karnik NN, Mendel JM (2001) Centroid of a type-2 fuzzy set. Inf Sci 132(1–4):195–220
Khosravi A, Nahavandi S (2014) Load forecasting using interval type-2 fuzzy logic systems: optimal type reduction. IEEE Trans Ind Inf 10(2):1055–1063
Linda O, Manic M (2012) Monotone centroid flow algorithm for type reduction of general type-2 fuzzy sets. IEEE Trans Fuzzy Syst 20(5):805–819
Liu FL (2008) An efficient centroid type reduction strategy for general type-2 fuzzy logic system. Inf Sci 178(9):2224–2236
Liu X, Mendel JM, Wu DR (2012) Study on enhanced Karnik–Mendel algorithms: initialization explanations and computation improvements. Inf Sci 184(1):75–91
Mathews JH, Fink KD (2004) Numerical methods using matlab. Prentice-Hall Inc., Upper Saddle River
Melin P, Gonzalez CI, Castro JR, Mendoza O, Castillo O (2014) Edge-detection method for image processing based on generalized type-2 fuzzy logic. IEEE Trans Fuzzy Syst 22(6):1515–1525
Mendel JM (2001) Uncertain rule-based fuzzy logic systems: introduction and new directions. Prentice-Hall, Englewood Cliffs
Mendel JM (2007) Type-2 fuzzy sets and systems: an overview. IEEE Comput Intell Mag 2007 2(2):20–29
Mendel JM (2013) On KM algorithms for solving type-2 fuzzy set problems. IEEE Trans Fuzzy Syst 21(3):426–446
Mendel JM (2014) General type-2 fuzzy logic systems made simple: a tutorial. IEEE Trans Fuzzy Syst 22(5):1162–1182
Mendel JM, John RB (2002) Type-2 fuzzy sets made simple. IEEE Trans Fuzzy Syst 10(2):117–127
Mendel JM, Liu F (2007) Super-exponential convergence of the Karnik–Mendel algorithms for computing the centroid of an interval type-2 fuzzy set. IEEE Trans Fuzzy Syst 15(2):309–320
Mendel JM, Liu X (2013) Simplified interval type-2 fuzzy logic systems. IEEE Trans Fuzzy Syst 21(6):1056–1069
Mendel JM, Wu HW (2006) Type-2 fuzzistics for symmetric interval type-2 fuzzy sets: part 1, forward problems. IEEE Trans Fuzzy Syst 14(6):781–792
Mendel JM, Liu FL, Zhai DY (2009) \(\alpha \)-Plane representation for type-2 fuzzy sets: theory and applications: theory and applications. IEEE Trans Fuzzy Syst 17(5):1189–1207
Niewiadomski A (2010) On finity, countability, cardinalities, and cylindric extensions of type-2 fuzzy sets in linguistic summarization of databases. IEEE Trans Fuzzy Syst 18(3):532–545
Olivas F, Valdez F, Castillo O et al (2016) Dynamic parameter adaptation in particle swarm optimization using interval type-2 fuzzy logic. Soft Comput 20(3):1057–1070
Sanchez MA, Castillo O, Castro JR (2015) Generalized type-2 fuzzy systems for controlling a mobile robot and a performance comparison with interval type-2 and type-1 fuzzy systems. Expert Syst Appl 42(14):5904–5914
Wagner C, Hagras H (2010) Toward general type-2 fuzzy logic systems based on zSlices. IEEE Trans Fuzzy Syst 18(4):637–660
Wang T, Chen Y, Tong SC (2008) Fuzzy reasoning models and algorithms on type-2 fuzzy sets. Int J Innov Comput Inf Control 4(10):2451–2460
Wu DR, Mendel JM (2009) Enhanced Karnik–Mendel algorithms. IEEE Trans Fuzzy Syst 17(4):923–934
Zarandi MHF, Rezaee B, Turksen IB, Neshat E (2009) A type-2 fuzzy rule-based expert system model for stock price analysis. Expert Syst Appl 36(1):139–154
Zhai DY, Hao MS, Mendel JM (2012) Universal image noise removal filter based type-2 fuzzy logic system and QPSO. Int J Uncertain Fuzziness Knowl Based Syst 20(supp02):207–232
Acknowledgements
This paper is partially sponsored by the Natural Science Foundation of China (No. 61374113) and Fundamental Research Funds for Liaoning’s Universities (No. JL201615410). The author is so thankful to Prof. J. M. Mendel, who has offered the author some worthy suggestions.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
All authors declare that they have no conflict of interest.
Additional information
Communicated by V. Loia.
Rights and permissions
About this article
Cite this article
Chen, Y., Wang, D. Study on centroid type-reduction of general type-2 fuzzy logic systems with weighted enhanced Karnik–Mendel algorithms. Soft Comput 22, 1361–1380 (2018). https://doi.org/10.1007/s00500-017-2938-3
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00500-017-2938-3