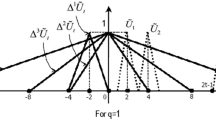
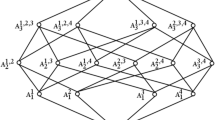
Abstract
An \(n \times n \) interval matrix \({\mathcal {A}}= [\underline{A},\overline{A}]\) is called to be a fuzzy interval matrix if \(0 \le \underline{A}_{ij} \le \overline{A}_{ij}\le 1\) for all \(1 \le i, j \le n\). In this paper, we proposed the notion of max-min algebra of fuzzy interval matrices. We show that the max-min powers of a fuzzy interval matrix either converge or oscillate with a finite period. Conditions for limiting behavior of powers of a fuzzy interval matrix are established. Some properties of fuzzy interval matrices in max-min algebra are derived. Necessary and sufficient conditions for the powers of a fuzzy interval matrices in max-min algebra to be nilpotent are proposed as well.
Similar content being viewed by others
Explore related subjects
Discover the latest articles, news and stories from top researchers in related subjects.References
Abdullah L, Najib L (2016) A new preference scale mcdm method based on interval-valued intuitionistic fuzzy sets and the analytic hierarchy process. Soft Comput 20:511–523
Akyar E, Akyar H, Diizce SA (2011) Brown-Robinson method for interval games. Soft Comput 15:2057–2064
Alefeld G, Herzberger J (1983) Introduction to interval computations. Academic Press, New York
Allahviranloo T, Ghanbari M (2012) A new approach to obtain algebaic solution of interval linear systems. Soft Comput 16:121–133
Collins WD, Hu C (2008) Studying interval valued matrix games with fuzzy logic. Soft Comput 12:147–155
Dong Y, Chen X, Li C-C, Hong W-C, Xu Y (2015) Consistency issues of interval pairwise comparison matrices. Soft Comput 19:2321–2335
Gavalec M, Plavka J, Tomášková H (2014) Interval eigenproblem in max-min algebra. Linear Algebra Appl 440:24–33
Hashimoto H (1982) Reduction of a nilpotent fuzzy matrix. Inf Sci 27:233–243
Hashimoto H (1983) Convergence of powers of a fuzzy transitive matrix. Fuzzy Sets Syst 9:153–160
Hashimoto H (1985) Transitivity of generalized fuzzy matrices. Fuzzy Sets Syst 17:83–90
Lur Y-Y, Pang C-T, Guu S-M (2003) On simultaneously nilpotent fuzzy matrices. Linear Algebra Appl 367:37–45
Lur Y-Y, Pang C-T, Guu S-M (2004) On nilpotent fuzzy matrices. Fuzzy Sets Syst 145:287–299
Mayer G (1984) On the convergence of powers of interval matrices. Linear Algebra Appl 58:201–216
Myšková H, Plavka J (2015) On the weak robustness of interval fuzzy matrices. Linear Algebra Appl 474:243–256
Pang C-T, Lur Y-Y (2008) On the stability of Takagi-Sugeno free fuzzy system with time-varying Uncertainty. IEEE Trans Fuzzy Syst 16(1):162–170
Pang C-T, Lur Y-Y, Guu S-M (2002) A new proof of Mayer’s theorem. Linear Algebra Appl 350:273–278
Shih M-H, Lur Y-Y, Pang C-T (1998) An inequality for the spectral radius of an interval matrix. Linear Algebra Appl 274:27–36
Thomason MG (1977) Convergence of powers of a fuzzy matrix. J Math Anal Appl 57:476–480
Acknowledgements
The first author’s research is supported in part by MOST 104-2410-H-238-003. The third author’s research is supported in part by MOST 104-2115-M-238-001.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
The authors declare that there is no conflict of interest.
Additional information
Communicated by M. Anisetti.
Rights and permissions
About this article
Cite this article
Wu, YK., Liu, CC. & Lur, YY. On the power sequence of a fuzzy interval matrix with max-min operation. Soft Comput 22, 1615–1622 (2018). https://doi.org/10.1007/s00500-018-3006-3
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00500-018-3006-3