Skip to main content
Springer Nature Link
Log in

A two-stage consensus reaching model for group decision making with reciprocal fuzzy preference relations

  • Methodologies and Application
  • Published:
Soft Computing Aims and scope Submit manuscript

Abstract

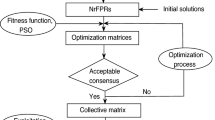
Reciprocal fuzzy preference relation (FPR) is a hot topic in the research field of group decision making (GDM). Within the framework of GDM, a two-stage consensus reaching model is proposed to modify the decision makers’ (DMs’) FPRs. In the first stage which is called consistency improving stage, a consistency index and an iterative algorithm are employed to measure and improve individual consistency, respectively. In each iteration of the algorithm, only one pair of preference values, which deviates the most from the corresponding elements in the consistent FPR matrix, are modified to keep the DM’s original information as much as possible. In the second stage which is called consensus reaching stage, individual consensus index and group consensus index are applied to measure consensus. A convex quadratic programming model is developed to help DMs reach consensus. Some desired properties of the model are also investigated and testified. What’s more, the final individual consistency is also limited to an acceptable threshold. Finally, a practical example is used to illustrate the validity of the proposed consensus model.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3

Similar content being viewed by others

Explore related subjects

Discover the latest articles, news and stories from top researchers in related subjects.

References

  • Alonso S, Herrera-Viedma E, Chiclana F, Herrera F (2010) A web based consensus support system for group decision making problems and incomplete preferences. Inf Sci 180:4477–4495

    Article  MathSciNet  Google Scholar 

  • Cabrerizo FJ, Moreno JM, Pérez IJ, Herrera-Viedma E (2010) Analyzing consensus approaches in fuzzy group decision making: advantages and drawbacks. Soft Comput 14:451–463

    Article  Google Scholar 

  • Cabrerizo FJ, Herrera-Viedma E, Pedrycz W (2013) A method based on PSO and granular computing of linguistic information to solve group decision making problems defined in heterogeneous contexts. Eur J Oper Res 230:624–633

    Article  MathSciNet  MATH  Google Scholar 

  • Cabrerizo FJ, Ureña R, Pedrycz W, Herrera-Viedma E (2014) Building consensus in group decision making with an allocation of information granularity. Fuzzy Sets Syst 255:115–127

    Article  MathSciNet  MATH  Google Scholar 

  • Cabrerizo FJ, Al-Hmouz R, Morfeq A, Balamash AS, Martínez M, Herrera-Viedma E (2017) Soft consensus measures in group decision making using unbalanced fuzzy linguistic information. Soft Comput 21:3037–3050

    Article  MATH  Google Scholar 

  • Cabrerizo FJ, Morente-Molinera JA, Pedrycz W, Taghavi A, Herrera-Viedma E (2018) Granulating linguistic information in decision making under consensus and consistency. Expert Syst Appl 99:83–92

    Article  Google Scholar 

  • Chiclana F, Herrera F, Herrera-Viedma E (1998) Integrating three representation models in fuzzy multipurpose decision making based on fuzzy preference relations. Fuzzy Sets Syst 97:33–48

    Article  MathSciNet  MATH  Google Scholar 

  • Chiclana F, Herrera-Viedma E, Herrera F, Alonso S (2007) Some induced ordered weighted averaging operators and their use for solving group decision-making problems based on fuzzy preference relations. Eur J Oper Res 182:383–399

    Article  MATH  Google Scholar 

  • Chiclana F, García JM, Moral MJ, Herrera-Viedma E (2013) A statistical comparative study of different similarity measures of consensus in group decision making. Inf Sci 221:110–123

    Article  MathSciNet  Google Scholar 

  • del Moral MJ, Chiclana F, Tapia JM, Herrera-Viedma E (2018) A comparative study on consensus measures in group decision making. Int J Intell Syst 33:1624–1638

    Article  Google Scholar 

  • Dong YC, Xu YF, Li HY, Feng B (2010a) The OWA-based consensus operator under linguistic representation models using position indexes. Eur J Oper Res 203:455–463

    Article  MATH  Google Scholar 

  • Dong YC, Zhang GQ, Hong WC, Xu JP (2010b) Consensus models for AHP group decision making under row geometric mean prioritization method. Decis Support Syst 49:281–289

    Article  Google Scholar 

  • Dong YC, Zha QB, Zhang HJ, Kou G, Fujita H, Chiclana F, Herrera-Viedma E (2018a) Consensus reaching in social network group decision making: research paradigms and challenges. Knowl Based Syst. https://doi.org/10.1016/j.knosys.2018.06.036

    Google Scholar 

  • Dong YC, Zhao SH, Zhang HJ, Chiclana F, Herrera-Viedma E (2018b) A self-management mechanism for non-cooperative behaviors in large-scale group consensus reaching processes. IEEE Trans Fuzzy Syst. https://doi.org/10.1109/TFUZZ.2018.2818078

    Google Scholar 

  • Herrera F, Herrera-Viedma E, Verdegay JL (1996a) A model of consensus in group decision making under linguistic assessments. Fuzzy Sets Syst 78:73–87

    Article  MathSciNet  MATH  Google Scholar 

  • Herrera F, Herrera-Viedma E, Verdegay JL (1996b) A rational consensus model in group decision making using linguistic assessments. Fuzzy Sets Syst 88:31–49

    Article  MATH  Google Scholar 

  • Herrera-Viedma E, Herrera F, Chiclana F (2002) A consensus model for multiperson decision making with different preference structures. IEEE Trans Syst Man Cybern Part A Syst Hum 32:394–402

    Article  MATH  Google Scholar 

  • Herrera-Viedma E, Herrera F, Chiclana F, Luque M (2004) Some issues on consistency of fuzzy preference relations. Eur J Oper Res 154:98–109

    Article  MathSciNet  MATH  Google Scholar 

  • Herrera-Viedma E, Martinez L, Mata F, Chiclana F (2005) A consensus support system model for group decision-making problems with multigranular linguistic preference relations. IEEE Trans Fuzzy Syst 13:644–658

    Article  Google Scholar 

  • Herrera-Viedma E, Alonso S, Chiclana F, Herrera F (2007) A consensus model for group decision making with incomplete fuzzy Preference Relations. IEEE Trans Fuzzy Syst 15:863–877

    Article  MATH  Google Scholar 

  • Kacprzyk J (1986) Group decision making with a fuzzy linguistic majority. Fuzzy Sets Syst 18:105–118

    Article  MathSciNet  MATH  Google Scholar 

  • Liu WQ, Dong YC, Chiclana F, Cabrerizo FJ, Herrera-Viedma E (2017) Group decision-making based on heterogeneous preference relations with self-confidence. Fuzzy Optim Decis Mak 16:429–447

    Article  MathSciNet  MATH  Google Scholar 

  • Ma J, Fan ZP, Jiang YP, Mao JY, Ma L (2006) A method for repairing the inconsistency of fuzzy preference relations. Fuzzy Sets Syst 157:20–33

    Article  MathSciNet  MATH  Google Scholar 

  • Önüt S, Efendigil T, Kara SS (2010) A combined fuzzy MCDM approach for selecting shopping center site: an example from Istanbul, Turkey. Expert Syst Appl 37:1973–1980

    Article  Google Scholar 

  • Orlovsky SA (1978) Decision-making with a fuzzy preference relation. Fuzzy Sets Syst 1:155–167

    Article  MathSciNet  MATH  Google Scholar 

  • Pérez IJ, Cabrerizo FJ, Alonso S, Dong YC, Chiclana F, Herrera-Viedma E (2018) On dynamic consensus processes in group decision making problems. Inf Sci 459:20–35

    Article  Google Scholar 

  • Roubens M (1997) Fuzzy sets and decision analysis. Fuzzy Sets Syst 90:199–206

    Article  MathSciNet  MATH  Google Scholar 

  • Saaty TL (1980) The analytic hierarchy process. McGraw-Hill, New York

    MATH  Google Scholar 

  • Tanino T (1984) Fuzzy preference orderings in group decision making. Fuzzy Sets Syst 33:117–131

    Article  MathSciNet  MATH  Google Scholar 

  • Wu J, Chiclana F (2014) Visual information feedback mechanism and attitudinal prioritisation method for group decision making with triangular fuzzy complementary preference relations. Inf Sci 279:716–734

    Article  MathSciNet  MATH  Google Scholar 

  • Wu ZB, Xu JP (2012) A concise consensus support model for group decision making with reciprocal preference relations based on deviation measures. Fuzzy Sets Syst 206:58–73

    Article  MathSciNet  MATH  Google Scholar 

  • Xu ZS, Cai XQ (2011) Group consensus algorithms based on preference relations. Inf Sci 181:150–162

    Article  MATH  Google Scholar 

  • Xu YJ, Da QL, Liu LH (2009) Normalizing rank aggregation method for priority of a fuzzy preference relation and its effectiveness. Int J Approx Reason 50:1287–1297

    Article  MathSciNet  MATH  Google Scholar 

  • Xu YJ, Li KW, Wang HM (2013) Distance-based consensus models for fuzzy and multiplicative preference relations. Inf Sci 253:56–73

    Article  MathSciNet  MATH  Google Scholar 

  • Xu YJ, Gupta JND, Wang HM (2014) The ordinal consistency of an incomplete reciprocal preference relation. Fuzzy Sets Syst 246:62–77

    Article  MathSciNet  MATH  Google Scholar 

  • Xu YJ, Chen L, Rodríguez RM, Herrera F, Wang HM (2016) Deriving the priority weights from incomplete hesitant fuzzy preference relations in group decision making. Knowl Based Syst 99:71–78

    Article  Google Scholar 

  • Xu YJ, Cabrerizo FJ, Herrera-Viedma E (2017) A consensus model for hesitant fuzzy preference relations and its application in water allocation management. Appl Soft Comput 58:265–284

    Article  Google Scholar 

  • Xu YJ, Liu X, Wang HM (2018a) The additive consistency measure of fuzzy reciprocal preference relations. Int J Mach Learn Cybern 9:1141–1152

    Article  Google Scholar 

  • Xu YJ, Wang QQ, Cabrerizo FJ, Herrera-Viedma E (2018b) Methods to improve the ordinal and multiplicative consistency for reciprocal preference relations. Appl Soft Comput 67:479–493

    Article  Google Scholar 

  • Yager RR (1988) On ordered weighted averaging aggregation operators in multicriteria decisionmaking. IEEE Trans Syst Man Cybern 18:183–190

    Article  MathSciNet  MATH  Google Scholar 

  • Zadeh LA (1983) A computational approach to fuzzy quantifiers in natural languages. Comput Math Appl 9:149–184

    Article  MathSciNet  MATH  Google Scholar 

  • Zhang BW, Dong YC, Xu JP (2014) Multiple attribute consensus rules with minimum adjustments to support consensus reaching. Knowl Based Syst 67:35–48

    Article  Google Scholar 

  • Zhang HJ, Dong YC, Herrera-Viedma E (2017) Consensus building for the heterogeneous large-scale GDM with the individual concerns and satisfactions. IEEE Trans Fuzzy Syst 26:884–898

    Article  Google Scholar 

Download references

Acknowledgements

The authors are very grateful to associate editor and the anonymous reviewers for their constructive comments and suggestions that have helped to improve the quality of this paper. This work was partly supported by the National Natural Science Foundation of China (NSFC) under Grants (No. 71471056), Qing Lan Project of Jiangsu Province.

Author information

Authors and Affiliations

  1. Business School, Hohai University, Nanjing, 211100, People’s Republic of China

    Yejun Xu & Nannan Wu

Authors
  1. Yejun Xu
    View author publications

    You can also search for this author inPubMed Google Scholar

  2. Nannan Wu
    View author publications

    You can also search for this author inPubMed Google Scholar

Corresponding author

Correspondence to Yejun Xu.

Ethics declarations

Conflict of interest

The authors declare that they have no conflict of interest.

Additional information

Communicated by V. Loia.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Xu, Y., Wu, N. A two-stage consensus reaching model for group decision making with reciprocal fuzzy preference relations. Soft Comput 23, 8057–8073 (2019). https://doi.org/10.1007/s00500-018-3442-0

Download citation

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00500-018-3442-0

Keywords