Abstract
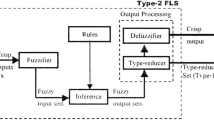
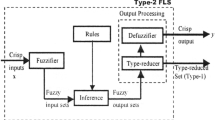
In recent years, researching on general type-2 fuzzy logic systems (GT2 FLSs) has become a hot topic as the development of alpha-planes representation of general type-2 fuzzy sets. The iterative Karnik–Mendel (KM) algorithms are used to perform the key block of type-reduction (TR) of GT2 FLSs. However, the KM algorithms are computationally intensive and time-consuming, which is not adapted to real-time applications. In the enhanced types of algorithms, the noniterative Nie–Tan (NT) algorithms decrease the computational cost greatly. Moreover, the closed-form Nie–Tan algorithms which calculate the outputs by averaging the lower and upper bounds of the membership functions have been proved to be actually an accurate algorithm for performing TR. The paper expands the NT algorithms to three different forms of weighted NT (WNT) algorithms according to the Newton–Cotes quadrature formulas of numerical integration techniques. Four computer simulation examples are adopted to analyze the performances of WNT algorithms when solving the type-reduction of general type-2 fuzzy logic systems. The proposed WNT algorithms have smaller absolute errors and faster convergence speed compared with NT algorithms, which provide the potential value for designers and adopters of GT2 FLSs.





























Similar content being viewed by others
Explore related subjects
Discover the latest articles, news and stories from top researchers in related subjects.References
Aisbett J, Rickard JT, Morgenthaler DG (2010) Type-2 fuzzy sets as functions on spaces. IEEE Trans Fuzzy Syst 18(4):841–844
Bel A, Wagner C, Hagras H (2013) Multiobjective optimization and comparison of nonsingleton type-1 and singleton interval type-2 fuzzy logic systems. IEEE Trans Fuzzy Syst 21(3):459–476
Biglarbegian M, Melek WW, Mendel JM (2010) On the stability of interval type-2 TSK fuzzy logic systems. IEEE Trans Syst Man Cybern Part B Cybern 40(3):798–818
Biglarbegian M, Melek WW, Mendel JM (2011) On the robustness of type-1 and interval type-2 fuzzy logic systems in modeling. Inf Sci 181(7):1325–1347
Bilgin A, Hagras H, Malibari A et al (2013) Towards a linear general type-2 fuzzy logic based approach for computing with words. Soft Comput 17(12):2203–2222
Castillo O, Melin P (2008) Intelligent systems with interval type-2 fuzzy logic. Int J Innov Comput Inf Control 4(4):771–783
Castillo O, Amador-Angulo L, Castro JR, Garcia-Valdez M (2016) A comparative study of type-1 fuzzy logic systems, interval type-2 fuzzy logic systems and generalized type-2 fuzzy logic systems in control problems. Inf Sci 354(part c):257–274
Cazarez-Castro NR, Aguilar LT, Castillo O (2012) Designing type-1 and type-2 fuzzy logic controllers via fuzzy Lyapunov synthesis for nonsmooth mechanical systems. Eng Appl Artif Intell 25(5):971–979
Chen Y (2018) Study on weighted Nagar–Bardini algorithms for centroid type-reduction of interval type-2 fuzzy logic systems. J Intell Fuzzy Syst 34(4):2417–2428
Chen Y, Wang DZ (2016) Type-reduction of interval type-2 fuzzy logic systems with weighted Karnik–Mendel algorithms. Control Theory and Applications 33(10):1327–1336
Chen Y, Wang DZ (2017) Forecasting by general type-2 fuzzy logic systems optimized with QPSO algorithms. Int J Control Autom Syst 15(6):2950–2958
Chen Y, Wang DZ (2018) Study on centroid type-reduction of general type-2 fuzzy logic systems with weighted enhanced Karnik–Mendel algorithms. Soft Comput 22(4):1361–1380
Chen Y, Wang DZ, Ning W (2015) Studies on centroid type-reduction algorithms for general type-2 fuzzy logic systems. Int J Innov Comput Inf Control 11(6):1987–2000
Chen Y, Wang DZ, Tong SC (2016) Forecasting studies by designing Mamdani interval type-2 fuzzy logic systems: with combination of BP algorithms and KM algorithms. Neurocomputing 174(part b):1133–1146
Chen Y, Wang DZ, Ning W (2018) Forecasting by TSK general type-2 fuzzy logic systems optimized with genetic algorithms. Opt Control Appl Methods 39(1):393–409
Coupland S, John R (2007) Geometric type-1 and type-2 fuzzy logic systems. IEEE Trans Fuzzy Syst 15(1):3–15
Gonzalez C, Castro JR, Melin P, Castillo O (2016a) An edge detection method based on generalized type-2 fuzzy logic. Soft Comput 20(2):773–784
Gonzalez C, Castro JR, Melin P, Castillo O (2016b) An edge detection method based on generalized type-2 fuzzy logic. Soft Comput 20(2):773–784
Gonzalez CI, Melin P, Castro JR, Mendoza O, Castillo O (2017) General type-2 fuzzy edge detection in the preprocessing of a face recognition system. Springer, Berlin
Greenfield S, Chiclana F (2013a) Accuracy and complexity evaluation of defuzzification strategies for the discretised interval type-2 fuzzy set. Int J Approx Reason 54(8):1013–1033
Greenfield S, Chiclana F (2013b) Defuzzification of the discretised generalised type-2 fuzzy set: experimental evaluation. Inf Sci 244(7):1–25
Greenfield S, Chiclana F, Coupland S, John R (2009) The collapsing method of defuzzification for discretised interval type-2 fuzzy sets. Inf Sci 179(3):2055–2069
Hsu CH, Juang CF (2013) Evolutionary robot wall-following control using type- 2 fuzzy controller with species-de-activated continuous ACO. IEEE Trans Fuzzy Syst 21(1):100–112
Karnik NN, Mendel JM (2001) Centroid of a type-2 fuzzy set. Inf Sci 132(1):195–220
Khosravi A, Nahavandi S (2014) Load forecasting using interval typ-2 fuzzy logic systems: optimal type reduction. IEEE Trans Industr Inf 10(2):1055–1063
Klir GJ, Yuan B (1995) Fuzzy sets and fuzzy logic: theory and applications. Prentice-Hall, Upper Saddle River, NJ, USA
Li JW, John R, Coupland S, Kendall G (2018) On Nie–Tan operator and type-reduction of interval type-2 fuzzy sets. IEEE Trans Fuzzy Syst 26(2):1036–1039
Liu FL (2008) An efficient centroid type-reduction strategy for general type-2 fuzzy logic system. Inf Sci 178(1):2224–2236
Liu XW, Mendel JM (2011) Connect Karnik–Mendel algorithms to root-finding for computing the centroid of an interval type-2 fuzzy set. IEEE Trans Fuzzy Syst 19(4):652–665
Liu XW, Mendel JM, Wu DR (2012) Study on enhanced Karnik–Mendel algorithms: initialization explanations and computation improvements. Inf Sci 184(1):75–91
Mathews JH, Fink KD (2004) Numerical Methods Using Matlab. Prentice-Hall Inc, Upper Saddle River, NJ
Melin P, Gonzalez CI, Castro JR, Mendoza O, Castillo O (2014) Edge-detection method for image processing based on generalized type-2 fuzzy logic. IEEE Trans Fuzzy Syst 22(6):1515–1525
Mendel JM (2001) Uncertain rule-based fuzzy logic systems: introduction and new directions. Prentice-Hall, Englewood Cliffs
Mendel JM (2009) Alpha-plane representation for type-2 fuzzy sets: theory and applications. IEEE Trans Fuzzy Syst 17(5):1189–1207
Mendel JM (2010) Comment on α-plane representation for type-2 fuzzy sets: theory and applications. IEEE Trans Fuzzy Syst 18(1):229–230
Mendel JM (2013a) On KM algorithms for solving type-2 fuzzy set problems. IEEE Trans Fuzzy Syst 21(3):426–446
Mendel JM (2013b) Simplified interval type-2 fuzzy logic systems. IEEE Trans Fuzzy Syst 21(6):1056–1069
Mendel JM (2014) General type-2 fuzzy logic systems made simple: a tutorial. IEEE Trans Fuzzy Syst 22(5):1162–1182
Mendel JM, John RB (2002) Type-2 fuzzy sets made simple. IEEE Trans Fuzzy Syst 10(2):117–127
Mendel JM, Liu FL (2007) Super-exponential convergence of the Karnik-Mendel algorithms for computing the centroid of an interval type-2 fuzzy set. IEEE Trans Fuzzy Syst 15(2):309–320
Mendel JM, Wu HW (2007a) Type-2 fuzzistics for symmetric interval type-2 fuzzy sets: Part 1, forward problems. IEEE Trans Fuzzy Syst 14(6):360–377
Mendel JM, Wu HW (2007b) New results about the centroid of an interval type-2 fuzzy set, including the centroid of a fuzzy granule. Inf Sci 177(2):360–377
Nie M, Tan WW (2008) Towards an efficient type-reduction method for interval type-2 fuzzy logic systems. In: IEEE international conference on fuzzy systems, pp 1425–1432
Olivas F, Valdez F, Castillo O et al (2016) Dynamic parameter adaptation in particle swarm optimization using interval type-2 fuzzy logic. Soft Comput 20(3):1057–1070
Ontiveros-Robles E, Melin P, Castillo O (2017) New methodology to approximate type-reduction based on a continuous root-finding Karnik Mendel algorithm. Algorithms 10(3):1–21
Ontiveros-Robles E, Melin P, Castillo O (2018) Comparative analysis of noise robustness of type-2 fuzzy logic controllers. Kybernetika 54(1):175–201
Sanchez MA, Castillo O, Castro JR (2015) Generalized type-2 fuzzy systems for controlling a mobile robot and a performance comparison with interval type-2 and type-1 fuzzy systems. Expert Syst Appl 42(14):5904–5914
Wagner C, Hagras H (2010) Toward general type-2 fuzzy logic systems based on zSlices. IEEE Trans Fuzzy Syst 18(4):637–660
Wagner C, Hagras H (2013) Slices based general type-2 fuzzy sets and systems, in advances in type-2 fuzzy sets and systems: theory and applications. In: Sadeghian A, Mendel JM, Tahayori H (eds) Springer, New York
Wang DZ, Chen Y (2018) Study on permanent magnetic drive forecasting by designing Takagi Sugeno Kang type interval type-2 fuzzy logic systems. Trans Inst Meas Control 40(6):2011–2023
Wang T, Chen Y, Tong SC (2008) Fuzzy reasoning models and algorithms on type-2 fuzzy sets. Int J Innov Comput Inf Control 4(10):2451–2460
Wu DR (2013) Approaches for reducing the computational cost of interval type-2 fuzzy logic systems: overview and comparisons. IEEE Trans Fuzzy Syst 21(1):80–99
Wu HW, Mendel JM (2002) Uncertainty bounds and their use in the design of interval type-2 fuzzy logic systems. IEEE Trans Fuzzy Syst 10(5):622–639
Wu DR, Mendel JM (2009) Enhanced Karnik–Mendel algorithms. IEEE Trans Fuzzy Syst 17(4):923–934
Wu DR, Nie M (2011) Comparison and practical implementations of type reduction algorithms for type-2 fuzzy sets and systems. In: IEEE international conference on fuzzy systems, pp 2131–3138
Acknowledgements
This paper is partially supported by the Natural Science Foundation of China (No. 61773188, No. 61803189), Liaoning Province Natural Science Foundation Guidance Project (No. 20180550056) and Fundamental Research Funds for Liaoning's Universities (No. JL201615410). The author is very obliged to Professor Jerry Mendel, who has offered the author some important suggestions.
Author information
Authors and Affiliations
Corresponding authors
Ethics declarations
Conflict of interest
No conflict exists. The authors declare that they have no conflict of interest
Ethical approval
This article does not contain any studies with human participants or animals performed by any of the authors.
Additional information
Communicated by V. Loia.
Publisher’s Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
About this article
Cite this article
Chen, Y., Wang, D. Study on centroid type-reduction of general type-2 fuzzy logic systems with weighted Nie–Tan algorithms. Soft Comput 22, 7659–7678 (2018). https://doi.org/10.1007/s00500-018-3551-9
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00500-018-3551-9