Abstract
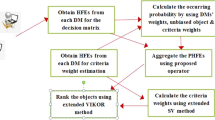
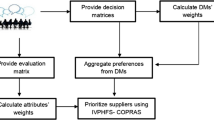
As a powerful extension to fuzzy set, hesitant fuzzy set (HFS) attracted many scholars in the recent times. The HFS had the ability to accept multiple membership values for a specific instance, which helped in handling uncertainty to a certain extent. However, the previous studies on the hesitant fuzzy theory consider only single occurring probability value for each element which is problematic for decision-makers (DMs) to associate an accurate occurring probability with each element. To alleviate this issue, in this paper, a new concept called interval-valued probabilistic hesitant fuzzy set (IVPHFS) is proposed. Some desirable properties of IVPHFS are also investigated. Further, a new aggregation operator called simple interval-valued probabilistic hesitant fuzzy weighted geometry (SIVPHFWG) is presented and some interesting properties are discussed. Following this, a new extension of statistical variance (SV) is put forward under IVPHFS for calculating the weights of each criterion. A new extension to the popular VIKOR (VlseKriterijumskaOptimizacijaKompromisnoResenje) method is also presented under IVPHFS for ranking objects. The practicality of the proposed decision framework is analyzed by presenting two illustrative examples, viz., supplier selection problem and smartphone selection problem. Finally, the strength and weakness of the proposed decision framework are realized by comparison with other methods.


Similar content being viewed by others
Explore related subjects
Discover the latest articles, news and stories from top researchers in related subjects.References
Beg I, Rashid T (2014) Group decision making using intuitionistic hesitant fuzzy sets. Int J Fuzzy Log Intell Syst 14(3):181−187. https://doi.org/10.5391/IJFIS.2014.14.3.181
Büyüközkan G, Göçer F (2017) Application of a new combined intuitionistic fuzzy MCDM approach based on axiomatic design methodology for the supplier selection problem. Appl Soft Comput J 52:1222–1238. https://doi.org/10.1016/j.asoc.2016.08.051
Büyüközkan G, Güleryüz S (2016) Multi criteria group decision making approach for smart phone selection using intuitionistic fuzzy TOPSIS. Int J Comput Intell Syst 9(4):709–725. https://doi.org/10.1080/18756891.2016.1204119
Chen N, Xu Z (2015) Hesitant fuzzy ELECTRE II approach: a new way to handle multi-criteria decision making problems. Inf Sci 292:175–197. https://doi.org/10.1016/j.ins.2014.08.054
Ding Z, Wu Y (2016) An improved interval-valued hesitant fuzzy multi-criteria group decision-making method and applications. Math Comput Appl 21(2):22. https://doi.org/10.3390/mca21020022
Fouladian M, Hendessi F, Pourmina MA (2016) Using AHP and interval VIKOR methods to gateway selection in integrated VANET and 3G heterogeneous wireless networks in sparse situations. Arab J Sci Eng 41(8):2787–2800. https://doi.org/10.1007/s13369-015-2010-5
Gupta P, Mehlawat MK, Grover N (2016) Intuitionistic fuzzy multi-attribute group decision-making with an application to plant location selection based on a new extended VIKOR method. Inf Sci 370–371(01):184–203. https://doi.org/10.1016/j.ins.2016.07.058
He Y, He Z (2015) Hesitant fuzzy power bonferroni means and their application to multiple attribute decision making. IEEE Trans Fuzzy Syst 23(5):1655–1668. https://doi.org/10.1109/TFUZZ.2015.2460750
Hu SK, Lu MT, Tzeng GH (2014) Exploring smart phone improvements based on a hybrid MCDM model. Expert Syst Appl 41(9):4401–4413. https://doi.org/10.1016/j.eswa.2013.12.052
Jiang F, Ma Q (2017) Multi-attribute group decision making under probabilistic hesitant fuzzy environment with application to evaluate the transformation efficiency. Appl Intell. https://doi.org/10.1007/s10489-017-1041-x
Krishankumar R, Ravichandran KS, Murthy KK, Saeid AB (2018) A scientific decision-making framework for supplier outsourcing using hesitant fuzzy information. Soft Comput. https://doi.org/10.1007/s00500-018-3346-z
Liang Decui, Liu Dun (2015) A novel risk decision making based on hesitant fuzzy information. IEEE Trans Fuzzy Syst 23(2):237–247
Liao H, Xu Z (2013) A VIKOR-based method for hesitant fuzzy multi-criteria decision making. Fuzzy Optim Decis Mak 12(4):373–392. https://doi.org/10.1007/s10700-013-9162-0
Liao H, Xu Z (2014a) Priorities of intuitionistic fuzzy preference relation based on multiplicative consistency. IEEE Trans Fuzzy Syst 22(6):1669–1681. https://doi.org/10.1109/TFUZZ.2014.2302495
Liao H, Xu Z (2014b) Subtraction and division operations over hesitant fuzzy sets. J Intell Fuzzy Syst 27(1):65–72. https://doi.org/10.3233/IFS-130978
Liao H, Xu Z (2015) Consistency of the fused intuitionistic fuzzy preference relation in group intuitionistic fuzzy analytic hierarchy process. Appl Soft Comput 35:812–826. https://doi.org/10.1016/j.asoc.2015.04.015
Liao H, Xu Z, Xu J (2014) An approach to hesitant fuzzy multi-stage multi-criterion decision making. Kybernetes 43(9/10):1447–1468. https://doi.org/10.1108/K-11-2013-0246
Lima Junior FR, Osiro L, Carpinetti LCR (2014) A comparison between fuzzy AHP and fuzzy TOPSIS methods to supplier selection. Appl Soft Comput J 21(August):194–209. https://doi.org/10.1016/j.asoc.2014.03.014
Liu S, Chan FTS, Ran W (2016) Decision making for the selection of cloud vendor: an improved approach under group decision-making with integrated weights and objective/subjective attributes. Expert Syst Appl 55:37–47. https://doi.org/10.1016/j.eswa.2016.01.059
Mahmoudi A, Sadi-Nezhad S, Makui A, Vakili MR (2016) An extension on PROMETHEE based on the typical hesitant fuzzy sets to solve multi-attribute decision-making problem. Kybernetes 45(8):1213–1231. https://doi.org/10.1108/K-10-2015-0271
Opricovic S, Tzeng GH (2004) Compromise solution by MCDM methods: a comparative analysis of VIKOR and TOPSIS. Eur J Oper Res 156(2):445–455. https://doi.org/10.1016/S0377-2217(03)00020-1
Opricovic S, Tzeng GH (2007) Extended VIKOR method in comparison with outranking methods. Eur J Oper Res 178(2):514–529. https://doi.org/10.1016/j.ejor.2006.01.020
Qian G, Wang H, Feng X (2013) Generalized hesitant fuzzy sets and their application in decision support system. Knowl Based Syst 37:357–365. https://doi.org/10.1016/j.knosys.2012.08.019
Saaty TL (1990) How to make a decision: analytical hierarchy process. Eur J Oper Res 48:9–26
Saaty TL, Ozdemir MS (2003) Why the magic number seven plus or minus two. Math Comput Model 38(3):233–244. https://doi.org/10.1016/S0895-7177(03)90083-5
Shemshadi A, Shirazi H, Toreihi M, Tarokh MJ (2011) A fuzzy VIKOR method for supplier selection based on entropy measure for objective weighting. Expert Syst Appl 38(10):12160–12167. https://doi.org/10.1016/j.eswa.2011.03.027
Spearman C (1904) The proof and measurement of association between two things. Am J Psychol 15(1):72–101
Taciana C, Gussen G (2015) Hesitant fuzzy analytic hierarchy process. In: IEEE international conference on fuzzy system, pp 1–7
Torra V (2010) Hesitant fuzzy sets. Int J Intell Syst 25(2):529–539. https://doi.org/10.1002/int
Torra V, Narukawa Y (2009) On hesitant fuzzy sets and decision. In: IEEE international conference on fuzzy systems, pp 1378–1382. http://doi.org/10.1109/FUZZY.2009.5276884
Wang C, Li Q, Zhou X, Yang T (2014) Hesitant triangular fuzzy information aggregation operators based on bonferroni means and their application to multiple attribute decision making. Sci World J. https://doi.org/10.1155/2014/648516
Wei G (2012) Hesitant fuzzy prioritized operators and their application to multiple attribute decision making. Knowl Based Syst 31:176–182. https://doi.org/10.1016/j.knosys.2012.03.011
Xia M, Xu Z (2011) Hesitant fuzzy information aggregation in decision making. Int J Approx Reason 52(3):395–407. https://doi.org/10.1016/j.ijar.2010.09.002
Xia M, Xu Z (2012) Entropy/cross entropy-based group decision making under intuitionistic fuzzy environment. Inf Fus 13(1):31–47. https://doi.org/10.1016/j.inffus.2010.12.001
Xu Z (2014). Hesitant fuzzy sets theory. Studies in fuzziness and soft computing, vol 314. http://doi.org/10.1007/978-3-319-04711-9
Xu Z, Zhang X (2013) Hesitant fuzzy multi-attribute decision making based on TOPSIS with incomplete weight information. Knowl Based Syst 52:53–64. https://doi.org/10.1016/j.knosys.2013.05.011
Xu Z, Zhou W (2016) Consensus building with a group of decision makers under the hesitant probabilistic fuzzy environment. Fuzzy Optim Decis Mak 16(4):1–23. https://doi.org/10.1007/s10700-016-9257-5
Zhang X, Xu Z (2015) Hesitant fuzzy QUALIFLEX approach with a signed distance-based comparison method for multiple criteria decision analysis. Expert Syst Appl 42(2):873–884. https://doi.org/10.1016/j.eswa.2014.08.056
Zhang Y, Wang Y, Wang J (2014) Objective attributes weights determining based on shannon information entropy in hesitant fuzzy multiple attribute decision making. Math Probl Eng. https://doi.org/10.1155/2014/463930
Zhang S, Xu Z, He Y (2017) Operations and integrations of probabilistic hesitant fuzzy information in decision making. Inf Fus 38:1–11. https://doi.org/10.1016/j.inffus.2017.02.001
Zhou X, Li Q (2014) Multiple attribute decision making based on hesitant fuzzy Einstein geometric aggregation operators. J Appl Math. https://doi.org/10.1155/2014/745617
Zhou W, Xu Z (2017a) Expected hesitant VaR for tail decision making under probabilistic hesitant fuzzy environment. Appl Soft Comput J 60:297–311. https://doi.org/10.1016/j.asoc.2017.06.057
Zhou W, Xu Z (2017b) Group consistency and group decision making under uncertain probabilistic hesitant fuzzy preference environment. Inf Sci 414:276–288. https://doi.org/10.1016/j.ins.2017.06.004
Zhou W, Xu ZS (2017c) Probability calculation and element optimization of probabilistic hesitant fuzzy preference relations based on expected consistency. IEEE Trans Fuzzy Syst. https://doi.org/10.1109/TFUZZ.2017.2723349
Zhu B, Xu Z, Xia M (2012) Dual hesitant fuzzy sets. J Appl Math. https://doi.org/10.1155/2012/879629
Acknowledgements
The first author would like to thank University Grants Commission for their financial aid from Rajiv Gandhi National Fellowship with Grant No. F./2015-17/RGNF-2015-17-TAM-83, and the second author would like to thank Department of Science and Technology, Ministry of Science and Technology, Government of India, for their cloud infrastructure under the FIST programme with Grant No. SR/FST/ETI-349/2013. The authors also thank the editor and the anonymous reviewer(s) for their insightful comments which improved the quality of the paper.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
All authors declare that there is no conflict of interest.
Ethical approval
This article does not contain any studies with human participants or animals performed by any of the authors.
Informed consent
Informed consent was obtained from all participants included in the study.
Additional information
Communicated by V. Loia.
Rights and permissions
About this article
Cite this article
Krishankumar, R., Ravichandran, K.S., Kar, S. et al. Interval-valued probabilistic hesitant fuzzy set for multi-criteria group decision-making. Soft Comput 23, 10853–10879 (2019). https://doi.org/10.1007/s00500-018-3638-3
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00500-018-3638-3