Abstract
The paper outlines the production policies for maximum profit of a firm producing imperfect economic lot size with time-dependent fuzzy defective rate under the respective country’s carbon emission rules. Generally in economic production lot-size models, defective production starts after the passage of some time from production commencement. So the starting time of producing defective units is normally uncertain and imprecise. Thus, produced defective units are fuzzy, partially reworked instantly and sold as fresh units. As a result, the inventory level at any time becomes fuzzy and the relation between the production, demand and inventory level becomes a fuzzy differential equation (FDE). Nowadays, different governments have made environmental regulations following the United Nations Framework Convention on Climate Change to reduce carbon emission. Some governments use cape and trade policy on emission. Due to this, firms are in fix how to optimize the production. If the firms produce more, the profit increases along with more emission and corresponding tax. Here, models are formulated as profit maximization problems using FDE, and the corresponding inventory and environmental costs are calculated using fuzzy Riemann integration. An \(\alpha \)-cut of average profits is obtained and the reduced multi-objective crisp problems are solved using intuitionistic fuzzy optimization technique. The models are illustrated numerically and results are presented graphically. Considering different carbon regulations, an algorithm for a firm management is presented to achieve the maximum profit. Real-life production problems for the firms in Annex I and developing countries are solved.






Similar content being viewed by others
Explore related subjects
Discover the latest articles, news and stories from top researchers in related subjects.Abbreviations
- ACEC:
-
Average carbon emission cost
- ACER:
-
Average carbon emission reward
- ATP:
-
Average total profit
- CE :
-
Carbon emission
- CEC:
-
Carbon emission cost
- CER:
-
Carbon emission reward
- EOQ:
-
Economic order quantity
- EPL:
-
Economic production lot size
- EPQ:
-
Economic production quantity
- FDE:
-
Fuzzy differential equation
- FRI:
-
Fuzzy Riemann integration
- IFN:
-
Intuitionistic fuzzy number
- IFOT:
-
Intuitionistic fuzzy optimization technique
- IFS:
-
Intuitionistic fuzzy set
- MOOP:
-
Multi-objective optimization problem
- MOP:
-
Multi-objective problem
- TFN:
-
Triangular fuzzy number
- UPC:
-
Unit production cost
References
Ahmadi MB, Kiani NA, Mikaeilvand N (2014) Laplace transform formula on fuzzy \(n\)th-order derivative and its application in fuzzy ordinary differential equations. Soft Comput 18(12):2461–2469. https://doi.org/10.1007/s00500-014-1224-x
Allahviranloo T, Chehlabi M (2015) Solving fuzzy differential equations based on the length function properties. Soft Comput 19(2):307–320. https://doi.org/10.1007/s00500-014-1254-4
Allahviranloo T, Abbasbandy S, Behzadi SS (2014) Solving nonlinear fuzzy differential equations by using fuzzy variational iteration method. Soft Comput 18(11):2191–2200. https://doi.org/10.1007/s00500-013-1193-5
Angelov PP (1997) Optimization in an intuitionistic fuzzy environment. Fuzzy Sets Syst 86(3):299–306. https://doi.org/10.1016/S0165-0114(96)00009-7
Atanassov KT (1986) Intuitionistic fuzzy sets. Fuzzy Sets Syst 20(1):87–96. https://doi.org/10.1016/S0165-0114(86)80034-3
Atanassov KT (2010) Intuitionistic fuzzy sets: theory and applications, 1st edn. Physica-Verlag GmbH, Heidelberg
Ben-Daya M (2002) The economic production lot-sizing problem with imperfect production processes and imperfect maintenance. Int J Prod Econ 76(3):257–264. https://doi.org/10.1016/S0925-5273(01)00168-2
Benjaafar S, Li Y, Daskin M (2013) Carbon footprint and the management of supply chains: insights from simple models. IEEE Trans Autom Sci Eng 10(1):99–116. https://doi.org/10.1109/TASE.2012.2203304
Bouchery Y, Ghaffari A, Jemai Z, Dallery Y (2012) Including sustainability criteria into inventory models. Eur J Oper Res 222(2):229–240. https://doi.org/10.1016/j.ejor.2012.05.004
Buckley JJ, Feuring T (1999) Introduction to fuzzy partial differential equations. Fuzzy Sets Syst 105(2):241–248. https://doi.org/10.1016/S0165-0114(98)00323-6 (Fuzzy analysis and related topics)
Chalco-Cano Y, Romn-Flores H (2009) Comparation between some approaches to solve fuzzy differential equations. Fuzzy Sets Syst 160(11):1517–1527. https://doi.org/10.1016/j.fss.2008.10.002 (Theme: analysis)
Chen X, Benjaafar S, Elomri A (2013) The carbon-constrained EOQ. Oper Res Lett 41(2):172–179. https://doi.org/10.1016/j.orl.2012.12.003
Chiu YP (2003) Determining the optimal lot size for the finite production model with random defective rate, the rework process, and backlogging. Eng Optim 35(4):427–437. https://doi.org/10.1080/03052150310001597783
Das B, Maiti M (2012) A volume flexible fuzzy production inventory model under interactive and simulation approach. Int J Math Oper Res 4(4):422–438. https://doi.org/10.1504/IJMOR.2012.048903
Das S, Dutta B, Guha D (2016) Weight computation of criteria in a decision-making problem by knowledge measure with intuitionistic fuzzy set and interval-valued intuitionistic fuzzy set. Soft Comput 20(9):3421–3442. https://doi.org/10.1007/s00500-015-1813-3
Das A, Bera UK, Maiti M (2018) Defuzzification and application of trapezoidal type-2 fuzzy variables to green solid transportation problem. Soft Comput 22(7):2275–2297. https://doi.org/10.1007/s00500-017-2491-0
De SK, Goswami A (2006) An eoq model with fuzzy inflation rate and fuzzy deterioration rate when a delay in payment is permissible. Int J Syst Sci 37(5):323–335. https://doi.org/10.1080/00207720600681112
Dey JK, Kar S, Maiti M (2005) An interactive method for inventory control with fuzzy lead-time and dynamic demand. Eur J Oper Res 167(2):381–397. https://doi.org/10.1016/j.ejor.2003.07.025
Du S, Zhu L, Liang L, Ma F (2013) Emission-dependent supply chain and environment-policy-making in the cap-and-trade system. Energy Policy 57:61–67. https://doi.org/10.1016/j.enpol.2012.09.042
Dubois D, Prade H (1988) Possibility theory. Springer, New York
Ezzati R, Maleknejad K, Khezerloo S, Khezerloo M (2015) Convergence, consistency and stability in fuzzy differential equations. Iran J Fuzzy Syst 12(3):95–112. https://doi.org/10.22111/ijfs.2015.2021
Gitinavard H, Ghaderi H, Pishvaee MS (2018) Green supplier evaluation in manufacturing systems: a novel interval-valued hesitant fuzzy group outranking approach. Soft Comput 22(19):6441–6460. https://doi.org/10.1007/s00500-017-2697-1
Guchhait P, Maiti MK, Maiti M (2013) A production inventory model with fuzzy production and demand using fuzzy differential equation: an interval compared genetic algorithm approach. Eng Appl Artif Intell 26(2):766–778. https://doi.org/10.1016/j.engappai.2012.10.017
Hayek PA, Salameh MK (2001) Production lot sizing with the reworking of imperfect quality items produced. Prod Plan Control 12(6):584–590. https://doi.org/10.1080/095372801750397707
He P, Zhang W, Xu X, Bian Y (2015) Production lot-sizing and carbon emissions under cap-and-trade and carbon tax regulations. J Clean Prod 103:241–248. https://doi.org/10.1016/j.jclepro.2014.08.102 (Carbon emissions reduction: policies, technologies, monitoring, assessment and modeling)
Hu JS, Zheng H, Guo CY, Ji YP (2010) Optimal production run length with imperfect production processes and backorder in fuzzy random environment. Comput Ind Eng 59(1):9–15. https://doi.org/10.1016/j.cie.2010.01.012
Hua G, Cheng T, Wang S (2011) Managing carbon footprints in inventory management. Int J Prod Econ 132(2):178–185. https://doi.org/10.1016/j.ijpe.2011.03.024
Jaber MY, Glock CH, Saadany AME (2013) Supply chain coordination with emissions reduction incentives. Int J Prod Res 51(1):69–82. https://doi.org/10.1080/00207543.2011.651656
Jana B, Roy TK (2007) Multi-objective intuitionistic fuzzy linear programming and its application in transportation model. Notes Intuit Fuzzy Sets 13(1):34–51
Khouja M, Mehrez A (1994) An economic production lot size model with imperfect quality and variable production rate. J Oper Res Soc 45(12):1405–1417
Lasdon LS, Waren AD, Jain A, Ratner M (1978) Design and testing of a generalized reduced gradient code for nonlinear programming. ACM Trans Math Softw (TOMS) 4(1):34–50
Lin TY (2010) An economic order quantity with imperfect quality and quantity discounts. Appl Math Model 34(10):3158–3165. https://doi.org/10.1016/j.apm.2010.02.004
Liu B, Iwamura K (1998) Chance constrained programming with fuzzy parameters. Fuzzy Sets Syst 94(2):227–237
Mandal M, Maiti M (2000) Inventory of damagable items with variable replenishment and stock-dependent demand. Asia-Pac J Oper Res 17(1):41
Mandal S, Maity K, Mondal S, Maiti M (2010) Optimal production inventory policy for defective items with fuzzy time period. Appl Math Model 34(3):810–822. https://doi.org/10.1016/j.apm.2009.06.031
Manna A, Das B, Dey J, Mondal S (2016) An EPQ model with promotional demand in random planning horizon: population varying genetic algorithm approach. J Intell Manuf 27(1):1–17
Mizukoshi MT, Barros LC, Chalco-Cano Y, Román-Flores H, Bassanezi RC (2007) Fuzzy differential equations and the extension principle. Inf Sci 177(17):3627–3635. https://doi.org/10.1016/j.ins.2007.02.039
Mondal M, Maiti MK, Maiti M (2013) A production-recycling model with variable demand, demand-dependent fuzzy return rate: a fuzzy differential equation approach. Comput Ind Eng 64(1):318–332. https://doi.org/10.1016/j.cie.2012.10.014
Roy A, Kar S, Maiti M (2010) A volume flexible production-policy for randomly deteriorating item with trended demand and shortages. Int J Prod Econ 128(1):188–199. https://doi.org/10.1016/j.ijpe.2010.07.010 (Integrating the global supply chain)
Sakawa M (1983) Interactive computer programs for fuzzy linear programming with multiple objectives. Int J Man Mach Stud 18(5):489–503
Salameh M, Jaber M (2000) Economic production quantity model for items with imperfect quality. Int J Prod Econ 64(1):59–64. https://doi.org/10.1016/S0925-5273(99)00044-4
Sana SS (2010) An economic production lot size model in an imperfect production system. Eur J Oper Res 201(1):158–170. https://doi.org/10.1016/j.ejor.2009.02.027
Song J, Leng M (2012) Analysis of the single-period problem under carbon emissions policies. Springer, New York, pp 297–313. https://doi.org/10.1007/978-1-4614-3600-3_13
Taleizadeh AA, Kalantari SS, Cárdenas-Barrón LE (2016) Pricing and lot sizing for an epq inventory model with rework and multiple shipments. TOP 24(1):143–155. https://doi.org/10.1007/s11750-015-0377-9
Wang X, Tang W (2009) Optimal production run length in deteriorating production processes with fuzzy elapsed time. Comput Ind Eng 56(4):1627–1632. https://doi.org/10.1016/j.cie.2008.10.012
Wu HC (2000) The fuzzy riemann integral and its numerical integration. Fuzzy Sets Syst 110(1):1–25. https://doi.org/10.1016/S0165-0114(97)00353-9
Zadeh L (1965) Fuzzy sets. Inf Control 8(3):338–353. https://doi.org/10.1016/S0019-9958(65)90241-X
Zadeh L (1999) Fuzzy sets as a basis for a theory of possibility. Fuzzy Sets Syst 100:9–34. https://doi.org/10.1016/S0165-0114(99)80004-9
Zhang B, Xu L (2013) Multi-item production planning with carbon cap and trade mechanism. Int J Prod Econ 144(1):118–127. https://doi.org/10.1016/j.ijpe.2013.01.024
Zhang C, Zhao R, Tang W (2009) Optimal run lengths in deteriorating production processes in random fuzzy environments. Comput Ind Eng 57(3):941–948. https://doi.org/10.1016/j.cie.2009.03.014
Acknowledgements
The authors are greatly indebted to the referees for their valuable observations and suggestions for improving the presentation of the paper.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
The authors declare that they have no conflict of interest.
Ethical approval
This article does not contain any studies with human participants or animals performed by any of the authors.
Additional information
Communicated by V. Loia.
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendices
Appendix A
1.1 Mathematical prerequisites
1.1.1 Possibility/necessity measure in fuzzy environment
Let \(\mathfrak {R}\) represent the set of real numbers and \({\tilde{A}}\) and \({\tilde{B}}\) be two fuzzy numbers with membership functions \(\mu _{{\tilde{A}}}\) and \(\mu _{{\tilde{B}}}\), respectively. Then, taking degree of uncertainty as the semantics of fuzzy number, according to Zadeh (1999), Dubois and Prade (1988) and Liu and Iwamura (1998):
where the abbreviation Pos represents possibility and \(\star \) is any one of the relations \(>, <, =, \le , \ge \). Analogously, if \({\tilde{B}}\) is a crisp number, say b, then \( \text{ Pos } ({\tilde{A}}\star b) = \hbox {sup}\{\mu _{{\tilde{A}}}(x),x \in R, x\star b\}\)
On the other hand, necessity measure of an event \({\tilde{A}}\star {\tilde{B}}\) is a dual of possibility measure and defined as: \( \text{ Nes } ({\tilde{A}}\star {\tilde{B}}) = 1- \text{ Pos } (\overline{{\tilde{A}}\star {\tilde{B}}})\nonumber \), where the abbreviation Nes represents necessity measure and \(\overline{{\tilde{A}}\star {\tilde{B}}}\) represents complement of the event \({\tilde{A}}\star {\tilde{B}}\).
According to Liu and Iwamura (1998), Lemmas 1 and 2 can be easily derived.
Lemma 1
If \({\tilde{a}}=(a_1,a_2,a_3)\) be a TFN (triangular fuzzy number) with \(0<a_1\) and b is a crisp number, \(pos({\tilde{a}} \le b)\ge \alpha \) iff \(\displaystyle \frac{b-a_1}{a_2-a_1} \ge \alpha \).
Lemma 2
If \({\tilde{a}}=(a_1,a_2,a_3)\) be a TFN with \(0<a_1\) and b is a crisp number, \(nes({\tilde{a}} \le b)\ge \alpha \) iff \(\displaystyle \frac{a_3-b}{a_3-a_2} \le 1- \alpha \).
1.2 Fuzzy extension principle (Zadeh 1965)
If \({\tilde{a}}\) , \({\tilde{b}}\)\(\subseteq \mathfrak {R}\) and \({\tilde{c}}=f({\tilde{a}},{\tilde{b}})\), where \(f:\mathfrak {R}\times \mathfrak {R}\rightarrow \mathfrak {R}\) is a binary operation, membership function \(\mu _{{\tilde{c}}}\) of \({\tilde{c}}\) is defined as
1.3 \(\alpha \)-Cut of a fuzzy number
\(\alpha \)-Cut of a fuzzy number \({\tilde{A}}\) in X is denoted by \(A[\alpha ]\) and is defined as the following crisp set
\(A[\alpha ]\) is a non-empty bounded closed interval contained in X and it can be denoted by \(A[\alpha ] = [A_L(\alpha ),A_R(\alpha )]\). \(A_L(\alpha )\) and \(A_R(\alpha )\) are the lower and upper bounds of the closed interval, respectively, and defined as
1.3.1 Intuitionistic fuzzy set (IFS) (Atanassov 1986, 2010)
Let \(X = {x_1, x_2, \ldots , x_n}\) be a finite universal set. An Atanassov’s IFS A is a set of ordered triples,
where \(\mu _A(x_i)\) and \(\nu _A(x_i)\) are functions mapping from X into [0, 1]. For each \(x_i\)\(\in \)X, \(\mu _A(x_i)\) represents the degree of membership and \(\nu _A(x_i)\) represents the degree of non-membership of the element \(x_i\) to the subset A of X. For the functions \(\mu _A(x_i)\) and \(\nu _A(x_i)\) mapping into [0, 1], the condition \(0 \le \mu _A(x_i) + \nu _A(x_i) \le 1 \) holds .
1.3.2 Fuzzy differential equation (FDE) (Buckley and Feuring 1999)
Consider the first-order ordinary differential equation
where \(k =(k_1,k_2,\dots k_n)\) is a vector of constants and t is in some interval I (closed and bounded) which contains zero. Let Eq. (37) have a unique solution
When \({\widetilde{k}} =({\widetilde{k}}_1,{\widetilde{k}}_2,\dots {\widetilde{k}}_n)\) is a vector of fuzzy numbers and \({\widetilde{C}}\) be another fuzzy number, Eq. (37) reduces to the following fuzzy differential equation (FDE),
Assuming that derivative of the unknown fuzzy function \({\widetilde{Y}}(t)\) exists, then according to Buckley and Feuring (1999),
is solution of (39) if its \(\alpha \)-cut \({\widetilde{Y}}(t)[\alpha ]=[Y_L(t,\alpha ),Y_R(t,\alpha )]\) satisfies the following conditions.
where \({\widetilde{f}}(t)[\alpha ]=[f_L(t,\alpha ),f_R(t,\alpha )]\), \({\widetilde{C}}[\alpha ]=[C_L(\alpha ),C_R(\alpha )]\) are obtained following Eq. (36) and membership function of \({\widetilde{Y}}(t)\) is obtained using fuzzy extension principle (35).
1.3.3 Fuzzy Riemann integration (FRI)
Wu (2000) defined integration of fuzzy mapping over crisp and fuzzy intervals. Depending upon the limits of integral, two types of FRIs are as follows:
Fuzzy Riemann integral of type-I (Wu 2000): let \({\tilde{f}}(x)\) be a closed and bounded fuzzy-valued function on [a, b] and \([f_L(\alpha ,x),f_R(\alpha ,x)]\) be \(\alpha \)-cut of \({\tilde{f}}(x)\)\(\forall x \in [a,b]\). If \(f_L(\alpha ,x)\) and \(f_R(\alpha ,x)\) are Riemann integrable on [a, b], \(\forall \alpha \), then the fuzzy Riemann integral \(\int \limits _{a}^{b}{\tilde{f}}(x)\mathrm{d}x\) is a closed fuzzy number and its \(\alpha \)-level set is given by
Fuzzy Riemann integral of type-II (Wu 2000): let \({\tilde{f}}({\tilde{x}})\) be a bounded and closed fuzzy-valued function defined on the closed fuzzy interval \([{\tilde{a}},{\tilde{b}}]\) and \({\tilde{f}}(x)\) be induced by \({\tilde{f}}({\tilde{x}})\). \([f_L(\alpha ,x),f_R(\alpha ,x)]\) be \(\alpha \)-cut of \({\tilde{f}}(x)\) and \({\tilde{f}}(x)\) is either non-negative or non-positive.
Case-1: If \({\tilde{f}}(x)\) is non-negative and \(f_L(\alpha ,x)\) and \(f_R(\alpha ,x)\) are Riemann integrable on \([a_R(\alpha ),b_L(\alpha )]\) and \([a_L(\alpha ),b_R(\alpha )]\), respectively, \(\forall \alpha \), then the fuzzy Riemann integral \(\int \nolimits _{{\tilde{a}}}^{{\tilde{b}}}{\tilde{f}}({\tilde{x}})\mathrm{d}{\tilde{x}}\) is a closed fuzzy number and its \(\alpha \)-level set is given by
Case-2: If \({\tilde{f}}(x)\) is non-positive and \(f_L(\alpha ,x)\) and \(f_R(\alpha ,x)\) are Riemann integrable on \([a_L(\alpha ),b_R(\alpha )]\) and \([a_R(\alpha ),b_L(\alpha )]\), respectively, \(\forall \alpha \), then the fuzzy Riemann integral \(\int \nolimits _{{\tilde{a}}}^{{\tilde{b}}}{\tilde{f}}({\tilde{x}})\mathrm{d}{\tilde{x}}\) is a closed fuzzy number and its \(\alpha \)-level set is given by
Appendix B
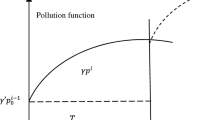
In the interval\([0,{\tilde{\tau }}]\):
\(\frac{\mathrm{d}I(t)}{\mathrm{d}t}=P - D \) with the initial condition I(0)=0. Solving this equation in crisp environment, we get, \(I(t)= (P - D)t\).
In the interval\([{\tilde{\tau }},t_1]\):
The fuzzy differential equation is \(\frac{\mathrm{d}{\widetilde{I}}(t)}{\mathrm{d}t}=P - D -(1-\theta )\gamma P(t-{\widetilde{\tau }})\) with fuzzy initial condition \({\widetilde{I}}({\tilde{\tau }})= (P - D){\tilde{\tau }}\). Solving this fuzzy differential equation, we get,
In the interval\([t_1,{\tilde{T}}]\):
The differential equation is \(\frac{\mathrm{d}I(t)}{\mathrm{d}t}= - D \) with boundary condition \(I(T)= 0\). Solving the above equation, we get \(I(t)=D(T-t)\). If \({\tilde{T}}\) is fuzzy in nature, then using the Jadeh’s extension principle we have,
Checking of Buckley–Feuring conditions:
In the interval\([{\tilde{\tau }},t_1]\):
Here, \({\tilde{\tau }}=(\tau _1,\tau _2,\tau _3)\) is a triangular fuzzy number having \(\alpha \)-cut \({\tilde{\tau }}[\alpha ]=[\tau _L,\tau _R]\), where \(\tau _L=\tau _1+\alpha (\tau _2-\tau _1)\) and \(\tau _R=\tau _3-\alpha (\tau _3-\tau _2)\). Also, \({\tilde{I}}(t)[\alpha ]=[I_L(\alpha ,t),I_R(\alpha ,t)]\), where \(I_{L}(\alpha ,t)=(P-D)t-\frac{(1-\theta )\gamma P}{2}(t-\tau _L)^2\) and \( I_{R}(\alpha ,t)=(P-D)t-\frac{(1-\theta )\gamma P}{2}(t-\tau _R)^2\).
Therefore, \(\frac{\mathrm{d}I_{L}(\alpha ,t)}{\mathrm{d}t}=(P-D)-(1-\theta )\gamma P(t-\tau _L)\) and \(\frac{\mathrm{d}I_{R}(\alpha ,t)}{\mathrm{d}t}=(P-D)-(1-\theta )\gamma P(t-\tau _R)\).
Differentiating the above equations with respect to \(\alpha \), we get
and
Also, \(\frac{\mathrm{d}I_{L}(1,t)}{\mathrm{d}t}=\frac{\mathrm{d}I_{R}(1,t)}{\mathrm{d}t}=(P-D)-(1-\theta )\gamma P(t-\tau _2)\).
Hence, all the equations and conditions defined by (41) and (42), respectively, are satisfied.
Appendix C
Individual minimum of the objective functions \(ACEC_k\) for all \(k=L,C,R\) is obtained and given in Table 9. Now we calculate \(L_L=4862.07\), \(L_C=5057.22\), \(L_R=5243.88\), \(U_L=4876.38\), \(U_C=5063.69\), \(U_R=5265.32\). we formulate the following problem as:

The solutions obtained for Eq. (45) are given in Table 10. Now we perform the Pareto-optimal solution test for strong or weak solutions. The Pareto-optimal results are presented in Table 11. In Table 11, the value of \(V^*\) is quite small, and hence, the optimal results in Table 11 are strong Pareto-optimal solution and can be accepted.
Rights and permissions
About this article
Cite this article
De, M., Das, B. & Maiti, M. EPL models with fuzzy imperfect production system including carbon emission: a fuzzy differential equation approach. Soft Comput 24, 1293–1313 (2020). https://doi.org/10.1007/s00500-019-03967-8
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00500-019-03967-8