Abstract
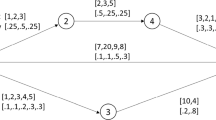
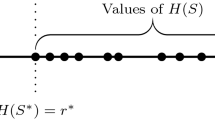
This paper characterizes the minimum risk path selection problem in an uncertain network. Assuming the accidental losses are the uncertain variables, we first present three types of uncertain risk indexes. After that, some uncertain risk programming models are built based on the proposed risk indexes. In order to obtain the minimum risk path, we convert these uncertain programming models to their corresponding deterministic forms by the operational law of uncertain variables. At last, a numerical example is given to demonstrate the models.

Similar content being viewed by others
Explore related subjects
Discover the latest articles, news and stories from top researchers in related subjects.References
Abkowitz M, Lepofsky M, Cheng P (1992) Selecting criteria for designating hazardous materials highway routes. Transp Res Rec 1333:30–35
Bronfman A, Marianov V, Paredes-Belmar G, Lüer-Villagra A (2015) The maximin hazmat routing problem. Eur J Oper Res 241:15–27
Díaz-Báñez J, Gómez F, Toussaint G (2005) Computing shortest paths for transportation of hazardous materials incontinuous spaces. J Food Eng 70(3):293–298
Ding S (2014) Uncertain minimum cost ow problem. Soft Comput 18(11):2201–2207
Erkut E, Gzara F (2008) Solving the hazmat transport network design problem. Comput Oper Res 35:2234–2247
Erkut E, Verter V (1995) A framework for hazardous materials transport risk assessment. Risk Anal 15(5):589–601
Erkut E, Verter V (1998) Modeling of transport risk for hazardous materials. Oper Res 46(5):625–642
Gao Y (2011) Shortest path problem with uncertain arc lengths. Comput Math Appl 62(6):2591–2600
Gao X, Gao Y (2013) Connectedness index of uncertain graphs. Int J Uncertain Fuzziness Knowl Based Syst 21(1):127–137
Gao X, Jia L (2017) Degree-constrained minimum spanning tree problem with uncertain edge weights. Appl Soft Comput 56:580–588
Gao X, Jia L, Kar S (2018) A new definition of cross-entropy for uncertain variables. Soft Comput 22(17):5617–5623
Han S, Peng Z, Wang S (2014) The maximum flow problem of uncertain network. Inf Sci 265:167–175 (2014)
Jonkman S, van Gelder P, Vrijling J (2003) An overview of quantitative risk measures for loss of life and economic damage. J Hazard Mater 99:1–30
Kahneman D, Tversky A (1979) Prospect theory: an analysis of decision under risk. Econometrica 47:263–292
Li S, Peng J, Zhang B (2013) The uncertain premium principle based on the distortion function. Insur Math Econ 53(2):317–324
Liu B (2007) Uncertain Theory, 2nd edn. Springer, Berlin
Liu B (2008) Fuzzy process, hybrid process and uncertain process. J Uncertain Syst 2:3–16
Liu B (2009a) Some research problems in uncertainty theory. J Uncertain Syst 3(1):3–10
Liu B (2009b) Theory and practice of uncertain programming, 2nd edn. Springer, Berlin
Liu B (2010b) Uncertain risk analysis and uncertain reliability analysis. J Uncertain Syst 4(3):163–170
Liu B (2010c) Uncertainty theory: a branch of mathematics for modeling human uncertainty. Springer, Berlin
Liu B (2010a) Uncertain set theory and uncertain inference rule with application to uncertain control. J Uncertain Syst 4(2):83–98
Liu B (2013b) Extreme value theorems of uncertain process with application to insurance risk model. Soft Comput 17(4):549–556
Liu B (2015) Uncertain Theory, 4th edn. Springer, Berlin
Liu Y, Ralescu DA (2018) Expected loss of uncertain random system. Soft Comput 22(17):5573–5578
Peng J (2013) Risk metrics of loss function for uncertain system. Fuzzy Optim Decis Mak 12(1):53–64
Peng J, Zhang B, Li S (2015) Towards uncertain network optimization. J Uncertain Anal Appl 3(4):1–19
Qin Z (2018) Uncertain random goal programming. Fuzzy Optim Decis Mak 17(4):375–386
Verter V, Kara B (2008) A path-based approach for hazmat transport network design. Manag Sci 54(1):29–40
Zhang B, Peng J (2012a) Euler index in uncertain graph. Appl Math Comput 218(20):10279–10288
Zhang B, Peng J (2012b) Uncertain programming model for Chinese postman problem with uncertain weights. Ind Eng Manag Syst 11(1):18–25
Zhou J, Yang F, Wang K (2014) An inverse shortest path problem on an uncertain graph. J Netw 9(9):2353–2359
Acknowledgements
This work is supported by the National Natural Science Foundation of China Grant Nos. 61873108, 61703438 and 11626234.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
The authors declare that they have no conflict of interest.
Ethical approval
This article does not contain any studies with human participants performed by any of the authors.
Additional information
Communicated by X. Li.
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
About this article
Cite this article
Li, S., Peng, J. & Zhang, B. The risk path selection problem in uncertain network. Soft Comput 24, 6375–6383 (2020). https://doi.org/10.1007/s00500-019-04132-x
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00500-019-04132-x